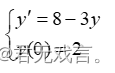| 实验目的及要求: 1、熟悉各种初值问题的算法,编出算法程序; 2、明确各种算法的精度寓所选步长有密切关系; 3、熟悉在Matlab平台上直接求解常微分方程初值问题。 | ||||||||
| 实验内容: 1、编写改进的欧拉公式通用子程序,取
求解初值问题 。 2、编写四阶经典龙格-库塔方法子程序,取
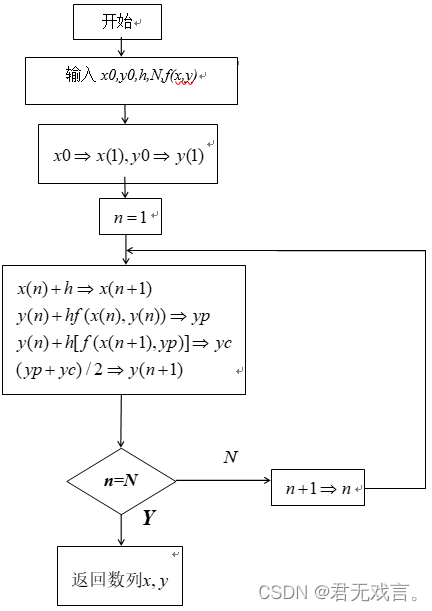
求解初值问题,并计算y(0.4)的近似值,要求小数点后保留4位有效数字。 | ||||||||
| 实验步骤与程序:
或者
被调用的ou_la_gaijin.m文件 function [x,y]=ou_la_gaijin(x0,y0,h,N,ydot_fun) x=zeros(1,N+1); y=zeros(1,N+1); x(1)=x0; y(1)=y0; for n=1:N x(n+1)=x(n)+h; ybar=y(n)+h*feval(ydot_fun,x(n),y(n)); y(n+1)=y(n)+(h/2)*(feval(ydot_fun,x(n),y(n))+feval(ydot_fun,x(n+1),ybar)); 运行的ou_la_gaijin1.m文件 ydot_fun=inline('1/(1+x^2)-2*y^2'); [x,y]=ou_la_gaijin(0,0,0.1,40,ydot_fun)
被调用的long_ge_ku_ta_4j.m文件 function [x,y]=long_ge_ku_ta_4j(x0,y0,h,N,fun) x=zeros(1,N+1); !生成矩阵 y=zeros(1,N+1); x(1)=x0; y(1)=y0; for n=1:N x(n+1)=x(n)+h; k1=feval(fun,x(n),y(n)); k2=feval(fun,x(n)+h/2,y(n)+(h*k1)/2); k3=feval(fun,x(n)+h/2,y(n)+(h*k2)/2); k4=feval(fun,x(n)+h,y(n)+h*k3) y(n+1)=y(n)+(h*(k1+2*k2+2*k3+k4))/6; end fun=@(x,y)8-3*y; [x,y]=long_ge_ku_ta_4j(0,2,0.2,5,fun) 运行的long_ge_ku_ta_4j_1.m文件 fun=@(x,y)8-3*y; !@()的意思是定义函数 [x,y]=long_ge_ku_ta_4j(0,2,0.2,5,fun) | ||||||||
| 运行结果:
| ||||||||
| 结果分析与讨论:
|
数学建模算法(基于matlab和python)之 改进的欧拉方法与四阶L-K方法(4/10)
news2026/2/13 17:52:44
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如若转载,请注明出处:http://www.coloradmin.cn/o/691947.html
如若内容造成侵权/违法违规/事实不符,请联系多彩编程网进行投诉反馈,一经查实,立即删除!相关文章
禽流感病毒防治VR模拟实训教学效率高-深圳华锐视点
对于临床兽医学实训而言,学生在实验教学中依托传统的教学方式已经无法满足学生的学习效率,理论知识和实验教学无法完美结合。 随着互联网数字化的飞速发展,数字化虚拟仿真教学兴起,有效的提升了传统教学的质量,学生在实…
Blender骨骼绑定
演示视频参考连接:Blender骨骼绑定教程3:清除绑定 & Deform & 权重修改_哔哩哔哩_bilibili
对给定人体Mesh建立骨骼的操作步骤:
在Blender中打开人体Mesh模型,并确保该模型处于object模式。或者使用快捷键“Shift A”并选择“骨骼…
【FFmpeg实战】视频容器
原文地址:https://alphahinex.github.io/2020/03/12/video-container/ 视频容器
我们常见的视频格式有 avi 或 mp4 等,这些所谓的视频格式,实际上指的只是视频容器的格式。就像 zip 格式的压缩包里面可以放置任意类型的文件一样,…
【初识 Docker | 中级篇】 Docker 中部署 Spring Boot 微服务详解
文章目录 前言一、生成 Docker 镜像1.编写Dockerfile2.构建镜像 二、启动容器1.运行服务2.测试 三、jar包映射部署1.更新Dockerfile文件2.构建镜像3.创建&启动容器 总结 前言
本文将为您详细介绍如何在Docker容器中部署Spring Boot服务。
首先,您需要为您的Sp…
Argo CD 实践教程 07
在本章中,我们将探讨如何设置用户访问Argo CD的权限,以及从终端或CI/CD管道连接CLI的选项,以及如何执行基于角色的访问控制。我们将查看单点登录(SSO)选项,通常这是一个需要付费的功能,但由于Ar…
Bean与@Bean注解
文章目录 一、背景与IoC二、注解Bean1、Bean注解用法2、Bean注解源码3、Bean注解演示 一、背景与IoC
之前的代码书写现状—耦合度偏高。如下图,业务层需要数据层实现类对象BookDaoImpl,于是自己new了一个,此时,当数据层类名改为B…
隐藏菜单之菜单和搜索
先看效果: 再看代码:
<!DOCTYPE html>
<html lang"en">
<head><meta charset"UTF-8"><title>菜单</title><style>/* css代码开始*/* {margin: 0;padding: 0;box-sizing: border-box;}b…
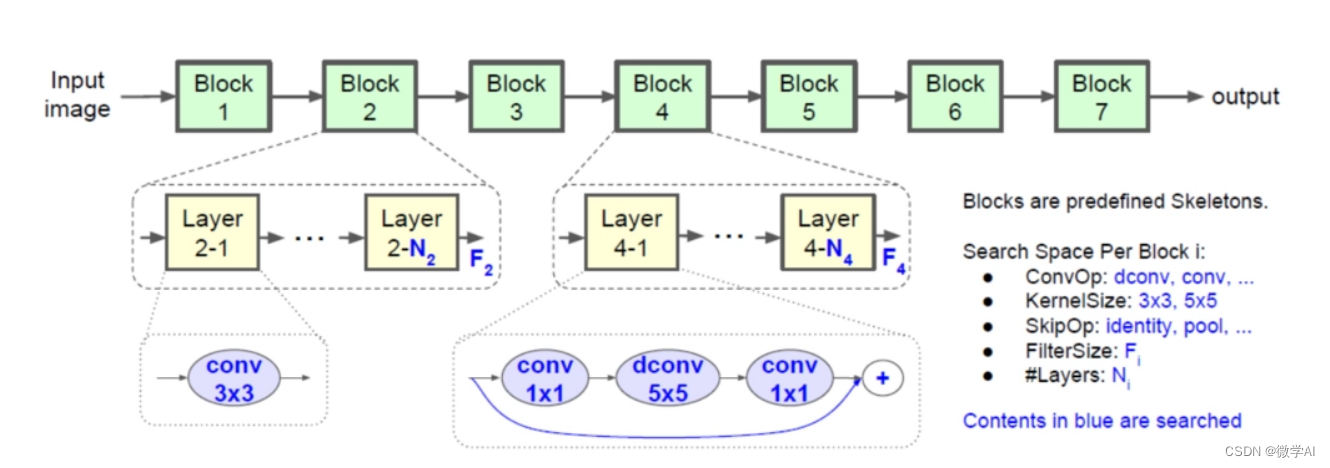
人工智能(pytorch)搭建模型15-手把手搭建MnasNet模型,并实现模型的训练与预测
大家好,我是微学AI,今天给大家介绍一下人工智能(pytorch)搭建模型15-手把手搭建MnasNet模型,并实现模型的训练与预测,本文将介绍MnasNet模型的原理,并使用PyTorch框架构建一个MnasNet模型用于图像分类任务,…
1、电商数仓(用户行为采集平台)数据仓库概念、用户行为日志、业务数据、模拟数据、用户行为数据采集模块、日志采集Flume
1、数据仓库概念
数据仓库( Data Warehouse ),是为企业制定决策,提供数据支持的。可以帮助企业,改进业务流程、提高产品质量等。 数据仓库的输入数据通常包括:业务数据、用户行为数据和爬虫数据等。 业务数…
Linux——使用第三方库链接的方式——动态式
回顾上文:
(122条消息) Linux使用第三方库链接的使用方式——静态式_橙予清的zzz~的博客-CSDN博客https://blog.csdn.net/weixin_69283129/article/details/131414804?spm1001.2014.3001.5502 上篇文章中,我讲到了关于链接第三方库作为静态库的使…
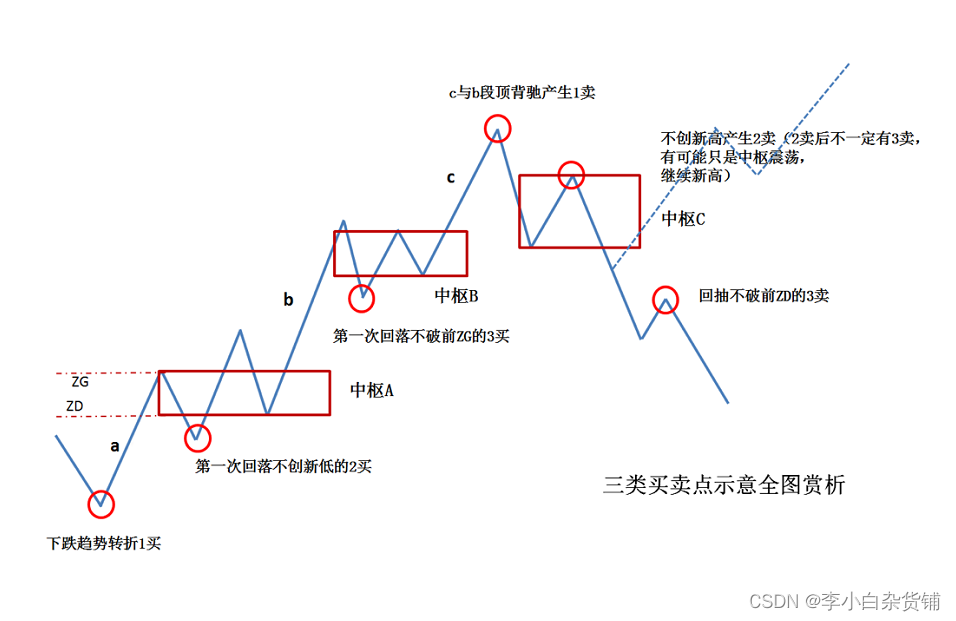
股票技术分析方法综述
文章目录 K线均线MACDKDJ和RSIBOLL线趋势理论、支撑位和压力位形态理论量价关系理论道氏理论波浪理论江恩理论缠论自定义指标 K线
K线的组合形态是K线技术分析中的重要部分,包括早晨之星、黄昏之星、红三兵、黑三兵等。
早晨之星:由三根K线组成&#x…
OpenGL 抗锯齿
1.简介
你可以看到,我们只是绘制了一个简单的立方体,你就能注意到它存在锯齿边缘。 可能不是非常明显,但如果你离近仔细观察立方体的边缘,你就应该能够看到锯齿状的图案。如果放大的话,你会看到下面的图案:…
软件测试的概念与过程(软件测试的历史、概念、结构、过程)
软件测试的概念与过程----软件测试的历史 软件测试的历史软件的概念软件的结构软件测试的过程 软件测试的历史 1、早期的的软件开发过程中,将测试“调试”,目的是纠正软件已经知道的故障,常常有开发人员自己去完成这部分工作。 2、1957年&…
Unity | HDRP高清渲染管线学习笔记:材质系统Lit着色器
目录
一、Lit着色器
1. Surface Options
2. Surface Inputs(表面输入)
3. Transparency Inputs
二、HDRP渲染优先级 我们可以把现实世界中的物体分成不透明物体和透明物体(其中包括透明或者半透明)。在实时渲染时,…
Debian二次开发网关支持Docker+RS485+网口
随着物联网技术的不断发展,瑞芯微边缘计算网关作为一种集成多种接口和功能的智能网关,逐渐成为了物联网领域中的热门产品。本文将详细介绍瑞芯微边缘计算网关的特点和优势,并探讨其在实际应用中的广泛应用。
瑞芯微Linux系统边缘计算网关是一…
【Java】 Java 私有接口方法的使用
本文仅供学习参考! 相关教程地址: https://www.baeldung.com/java-interface-private-methods https://www.geeksforgeeks.org/private-methods-java-9-interfaces/ https://www.runoob.com/java/java9-private-interface-methods.html 接口是定义一组方…
java之路—— SpringMVC的常用注解解析以及作用、应用
创作不易,真的希望能给个免费的小 文章目录 1、Controller2、RequestMapping3.GetMapping、PostMapping、PutMapping、DeleteMapping4. RequestParam5.PathVariable6.RequestHeader7.CookieValue8.RequestBody9.ResponseBody10.SessionAttribute11.ControllerAdvice…
二层、三层交换机是什么?有什么区别?
作者:Insist-- 个人主页:insist--个人主页 作者会持续更新网络知识和python基础知识,期待你的关注 前言
本文将讲解二层交换机和三层交换机是什么,以及他们的区别。
目录
一、二层交换机是什么?
二、二层交换机的主…