概述

定义：大概的定义就是prover可以向verifier证明自己给定的信息是大概率正确的，但是不泄露任何附加信息，包含信息本身。
举例
这里以一个比较经典的例子，即向红绿色盲（无法区分红色和绿色，看红色和绿色颜色差不多）证明两个小球（红球和绿球）的颜色是不同的。步骤如下，
首先让视觉正常的prover，把两个球分别放在色盲验证者的两只手上并记住球的颜色和位置，接着让色盲把手背过去，自行决定是否要交换球的位置，然后双手握球向prover展示，最后prover给出结论是否交换过。
整个例子很好的体现了零知识证明，验证者色盲在交互结束后除了能够相信手上的两个球颜色确实不同以外，无法获得任何信息，虽然这里会有个$\frac{1}{2}$的概率问题，但可以通过重复来降低概率。

分类

分类一：

• Proof of Knowledge：prover的确持有该知识。
• Proof of membership：可能不持有。

分类二：

• 交互式：交互式就是prover和verifier需要交互式的多次通信，才能生成一个proof用于验证。
• 非交互式：非交互式就是prover直接发送一个proof，verifier可以直接验证正确性。

基三个基本性质

• 可靠性（Soundness）： 如果verifier接受这个证明，那么这个statement就大概率是正确的。
• 完备性（Completeness）： 给定某个statement的有效证据, 如果prover和verifier均诚实运行协议，且这个statement是正确的, 那么verifier相信该statement的正确性。
• 零知识： prover能向verifier证明某个陈述的正确性而不泄露除正确性以外的其他任何信息，可以认为假设存在一个完全不知道任何相关信息的simulator，可以模拟出verifier对该证明进行验证。
  • 完美零知识性：整个协议中，证明者泄露给verifier的额外信息是0。
  • 统计学零知识性：额外信息可忽略
  • 基于算力假设：多项式时间内，额外信息是可忽略的

Sigma协议

是一种特殊的三轮零知识证明协议，基本流程如图

Sigma协议的性质

**知识合理性（Knowledge Soundness）：**传统的soundness是，如果verifier接受，那么大概率proof就是真的。而这里的Knowledge Soundness则是存在一个extractor，它可以和prover进行交互，如果prover有witness，那么extractor就可以通过多次的交互提取出这样一个witness。
换句话说就是，prover需要持有statement的相关的知识才能拿出可信的proof，即如果prover没有statement的知识，那么就无法说服verifier。相当于约束了prover，使得他无法骗人，如，prover说自己知道某个难题的解，verifier肯定不相信，那么就按照prover给的流程进行一步步推，最后发现确实可以，假如prover不知道解题的流程，那么是一定说服不了verifier的。
2-特殊合理性（2-Special Soundness）：

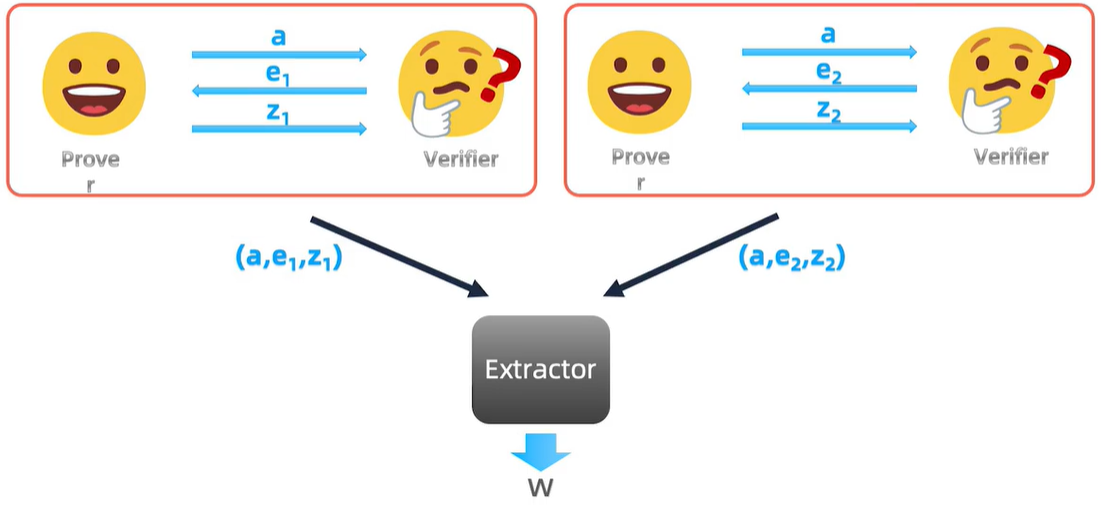
如果有两个transport，那么上面的两个$a$是一样的，而$e$和$z$则是不一样的，把这两个transport交给extractor就能提取出witness，同理需要k个transport的话，就是k-Special Soundness
特殊诚实验证者零知识性（SHZK，Special Honest verifuer Zero-knowledge）：
只能满足honest的verifier，malicious是不行的。

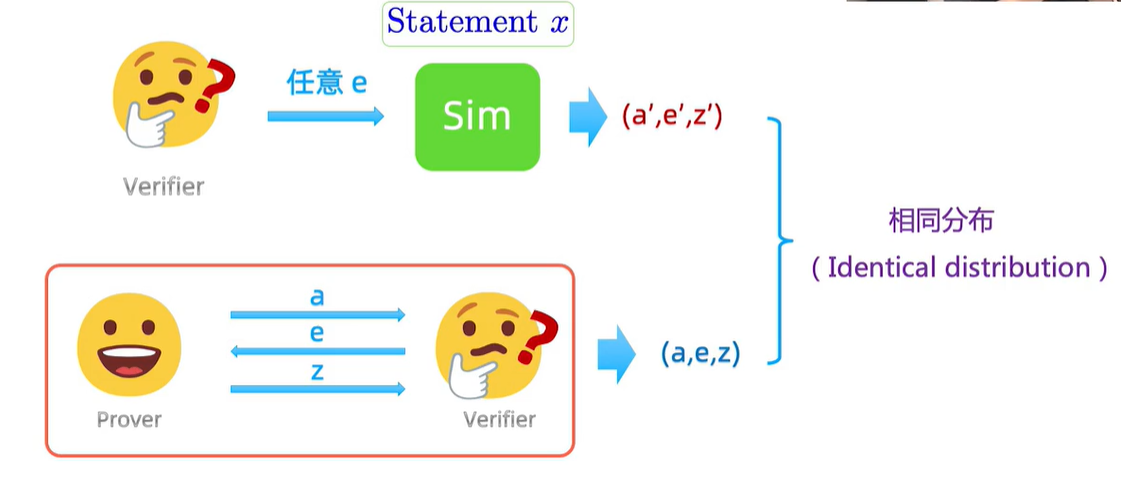
存在一个simulator，对于任意给定的一个challenge，也就是$e$，这个simulator都能输出一组$(a^{\prime },e,z^{\prime })$，和真正的prover与verifier交互基本无法区分。
简单说就是，整个协议的交互是不会泄露任何有用的东西，主要约束verifier，使得其除了结果以外一无所知。

一个例子-Schnorr协议

$G$是一个阶为素数$p$的一个乘法群（BTW，在椭圆曲线上面也是类似的），$g$则是它的生成元，$w$为私钥，$x=g^w$则为公钥，整个协议就是prover向verifier证明其拥有$PK$对应的$SK$，大致过程如图

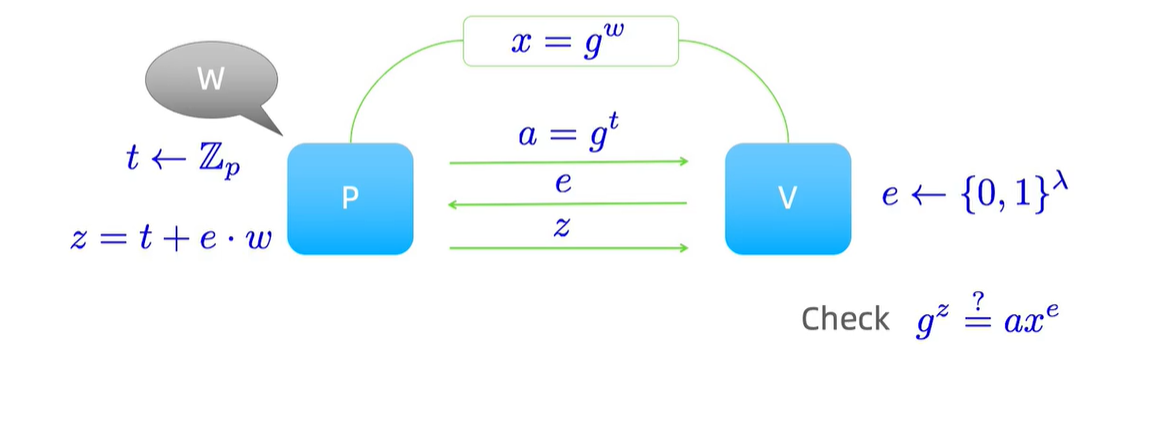
1. 首先prover随机选择一个随机数$t$，作用是用于保护私钥无法被verifier直接提取出来，然后计算$a=g^t$，发送给verifier。
2. verifier随机选择一个挑战$e$，发送给prover。
3. prover计算$z=t+e\cdot w$
4. verifier进行验证，即计算$g^z\stackrel{?}{=}a{x}^e$

证明

• Knowledge Soundness

在最后的验算中已经证明了，接下来证明

• 2- Speclai Soundness

即构造两个transport，看看extractor与之交互后能否提取出witness，如图

可以看到结果是可以提取出来的

• SHVZK

创建一个模拟器，它将模拟prover，给定任意一个挑战$e$后，会生成相应结果$(a,e,z)$

$z$是随机的，$g,x,e$都是已知的，则$a$是随机，和正常prover计算的$a=g^t$都是随机的，那么Sim和真实prover的所生成的参数是identical distribution的。
注意，Sim无法在真实世界使用，因为它少了一个order的信息，也就是真实世界执行顺序是定好的先给出$a$再给出$e$。如果证明发生在虚拟机环境中，那么证明是有风险的，因为虚拟机可以反复snapshot，然后rewind，相当于order不会严格的执行，且虚拟机的randness是用的主机的，那么这个randness 就可以被固定，从而导致知识$w$泄露。

Flat-shamir转换

采用Hash函数的方法将交互式零知识证明转换为非交互式零知识证明，这样就通过减少通信步骤而提高了通信的效率。对比交互式证明好处有二，
其一是verifier无需在线，
其二是可以同时向所有人证明。

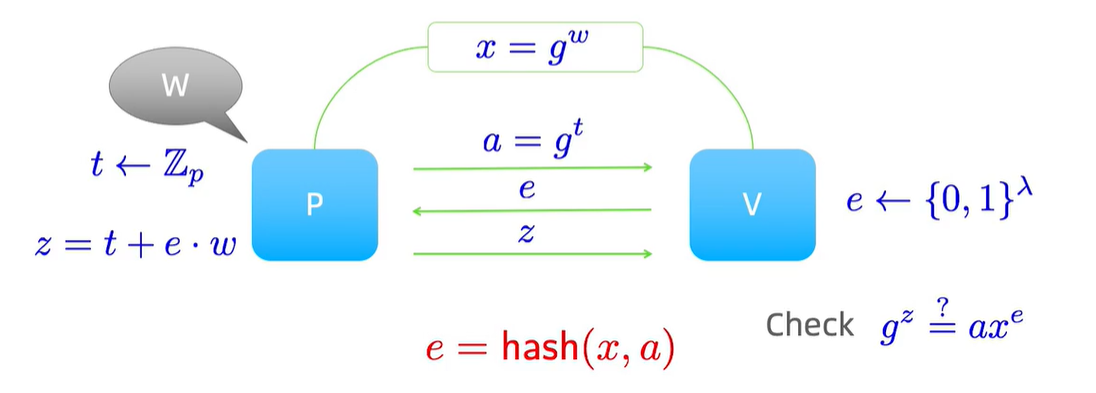
hash里面不仅仅是$a$，还要包括之前statement。
prover可以自己计算出一个$a$和$x$来“创造”出一个$e$（将它看作是verifier发送过来的），并计算$z$直接发送给verifier。verifier自己能够知道$a$和$x$，所以他也可以计算出$e$，然后收到来自prover的$z$，从而完成验证，整个过程就可以省略交互。

参考

隐私计算基础理论-零知识证明
初识「零知识」与「证明」（郭宇）
从交互到非交互式零知识证明
零知识证明：一个略微严肃的科普