C++进阶—二叉搜索树Key、Key-Value模型应用及二叉树OJ（非递归实现遍历）

news2024/11/19 8:46:41

 

目录

1、二叉树搜索模型实现及应用场景

1. 二叉搜索树Key模型及其应用

2. 二叉搜索树Key-Value模型及其应用

2、二叉树OJ

2.1 根据二叉树创建字符串

2.2 二叉树的层序遍历I

2.3 二叉树的层序遍历II

2.4 二叉树的最近公共祖先

2.5 二叉搜索树及双向链表

2.6 从前序与中序遍历序列构造二叉树

2.7 从中序与后序遍历序列构造二叉树

3、非递归实现二叉树遍历

3.1 非递归前序遍历

3.2 非递归实现中序遍历

3.3 非递归实现后序遍历

1、二叉树搜索模型实现及应用场景

1. 二叉搜索树Key模型及其应用

K模型：K模型即只有key作为关键码，结构中只需要存储Key即可，关键码即为需要搜索到的值。

 

比如：给一个单词word，判断该单词是否拼写正确，具体方式如下： 以词库中所有单词集合中的每个单词作为key，构建一棵二叉搜索树 在二叉搜索树中检索该单词是否存在，存在则拼写正确，不存在则拼写错误。

Key模型的实现（普通二叉搜索数的实现）：

template<class K>
	class BSTreeNode {
	public:
		BSTreeNode(const K& key)
			:_key(key)
			, _left(nullptr)
			, _right(nullptr)
		{
		}

		BSTreeNode<K>* _left;
		BSTreeNode<K>* _right;
		K _key;
	};

	//key
	template<class K>
	class BinarySearchTree {
		typedef BSTreeNode<K> Node;
		int _depth(Node* root) const {
			if (root == nullptr) {
				return 0;
			}
			int leftDepth = _depth(root->_left) + 1;
			int rightDepth = _depth(root->_right) + 1;
			return  leftDepth > rightDepth ? leftDepth : rightDepth;
		}
		int _nodeCount(Node* root) const {
			if (root == nullptr) {
				return 0;
			}
			int leftCount = _nodeCount(root->_left) + 1;
			int rightCount = _nodeCount(root->_right) + 1;
			return leftCount + rightCount - 1;
		}
		int _leafSize(Node* root) const {
			if (root == nullptr) {
				return 0;
			}
			if (root->_left == nullptr && root->_right == nullptr) {
				return 1;
			}
			int leftSize = _leafSize(root->_left);
			int rightSize = _leafSize(root->_right);
			return leftSize + rightSize;
		}
		void _destory(Node*& root) {
			if (root == nullptr) {
				return;
			}
			_destory(root->_left);
			_destory(root->_right);
			delete root;
			root = nullptr;
		}
		Node* _copy(Node* root) {
			if (root == nullptr) {
				return nullptr;
			}
			Node* copyRoot = new Node(root->_key);
			copyRoot->_left = _copy(root->_left);
			copyRoot->_right = _copy(root->_right);
			return copyRoot;
		}
	public:
		/*BinarySearchTree()
			:_root(nullptr)
		{

		}*/
		//拷贝构造也是构造，写了，编译器不在生成默认构造
		//强制编译器生成默认构造 —— c++11用法，default
		BinarySearchTree() = default;

		BinarySearchTree(const BinarySearchTree<K>& bst) {
			_root = _copy(bst._root);
		}
		~BinarySearchTree() {
			_destory(_root);
		}
		BinarySearchTree<K>& operator=(BinarySearchTree<K> bst) {
			std::swap(_root, bst._root);
			return *this;
		}

		int depth() const {
			return _depth(_root);
		}
		int nodeCount() const {
			return _nodeCount(_root);
		}
		int leafSize() const {
			return _leafSize(_root);
		}
		bool Insert(const K& key) {
			if (_root == nullptr) {
				_root = new Node(key);
				return true;
			}
			Node* cur = _root;
			Node* parent = nullptr;
			while (cur) {
				parent = cur;
				if (cur->_key > key) {
					cur = cur->_left;
				}
				else if (cur->_key < key) {
					cur = cur->_right;
				}
				else {
					return false;
				}
			}
			if (parent->_key > key) {
				parent->_left = new Node(key);
				return true;
			}
			else {
				parent->_right = new Node(key);
				return true;
			}
		}
		bool Find(const K& key) const {
			if (_root == nullptr) {
				return false;
			}
			Node* cur = _root;
			while (cur) {
				if (cur->_key > key) {
					cur = cur->_left;
				}
				else if (cur->_key < key) {
					cur = cur->_right;
				}
				else {
					return true;
				}
			}
			return false;
		}
		bool Erase(const K& key) {
			if (_root == nullptr) {
				return false;
			}
			Node* cur = _root;
			Node* parent = nullptr;
			while (cur) {
				if (cur->_key > key) {
					parent = cur;
					cur = cur->_left;
				}
				else if (cur->_key < key) {
					parent = cur;
					cur = cur->_right;
				}
				else {
					if (cur->_left == nullptr) {
						if (cur == _root) {
							_root = cur->_right;
						}
						else {
							if (cur == parent->_left) {
								parent->_left = cur->_right;
							}
							else {
								parent->_right = cur->_right;
							}
						}
						delete cur;
						cur = nullptr;
						return true;
					}
					else if (cur->_right == nullptr) {
						if (cur == _root) {
							_root = cur->_left;
						}
						else {
							if (cur == parent->_left) {
								parent->_left = cur->_left;
							}
							else {
								parent->_right = cur->_left;
							}
						}
						delete cur;
						cur = nullptr;
						return true;
					}
					else {
						//替换法删除 -- 右数最小节点
						Node* replace = cur->_right;
						Node* replaceParent = cur;
						while (replace->_left != nullptr) {
							replaceParent = replace;
							replace = replace->_left;
						}
						std::swap(cur->_key, replace->_key);
						if (replaceParent->_left == replace) {
							replaceParent->_left = replace->_right;
						}
						else {
							replaceParent->_right = replace->_right;
						}
						delete replace;
						return true;
					}
				}
			}
			return false;

		}

		void InOrder() {
			_InOrder(_root);
			cout << endl;
		}
		bool FindR(const K& key) const {
			return _FindR(_root, key);
		}
		bool InsertR(const K& key) {
			if (_root == nullptr) {
				_root = new Node(key);
				return true;
			}
			else {
				return _InsertR(_root, key);
			}
		}
		bool EraseR(const K& key) {
			return _EraseR(_root, key);
		}
	private:
		bool _EraseR(Node*& root, const K& key) {
			if (root == nullptr) {
				return false;
			}
			if (key > root->_key) {
				return  _EraseR(root->_right, key);
			}
			else if (key < root->_key) {
				return  _EraseR(root->_left, key);
			}
			else {
				//删除数据
				Node* del = root;
				if (root->_left == nullptr) {
					root = root->_right;
				}
				else if (root->_right == nullptr) {
					root = root->_left;
				}
				else {
					Node* replace = root->_right;
					while (replace->_left != nullptr) {
						replace = replace->_left;
					}
					std::swap(root->_key, replace->_key);
					return _EraseR(root->_right, key);
				}
				delete del;
				return true;
			}
		}
		bool _InsertR(Node*& root, const K& key) {
			if (root == nullptr) {
				root = new Node(key);
				return true;
			}

			if (key > root->_key) {
				return  _InsertR(root->_right, key);
			}
			else if (key < root->_key) {
				return  _InsertR(root->_left, key);
			}
			else {
				return false;
			}
		}
		bool _FindR(Node* root, const K& key) const {

			if (root == nullptr) {
				return false;
			}
			if (key > root->_key) {
				return _FindR(root->_right, key);
			}
			else if (key < root->_key) {
				return _FindR(root->_left, key);
			}
			else {
				return true;
			}
		}
		void _InOrder(Node* root) {
			if (root == nullptr) {
				return;
			}
			_InOrder(root->_left);
			cout << root->_key << " ";
			_InOrder(root->_right);
		}
	public:
		Node* GetRoot() {
			return _root;
		}
		void SetRoot(Node* root) {
			_root = root;
		}
	private:
		Node* _root = nullptr;
	};

	class Solution {
	public:
		void InOrder(BSTreeNode<int>* root, vector<BSTreeNode<int>*>& vt) {
			if (root == nullptr) {
				return;
			}
			InOrder(root->_left, vt);
			vt.push_back(root);
			InOrder(root->_right, vt);
		}
		BSTreeNode<int>* Convert(BSTreeNode<int>* pRootOfTree) {
			vector<BSTreeNode<int>*> vt;
			vt.push_back(nullptr);
			InOrder(pRootOfTree, vt);
			vt.push_back(nullptr);
			for (size_t i = 1; i < vt.size() - 1; ++i) {
				vt[i]->_left = vt[i - 1];
				vt[i]->_right = vt[i + 1];
			}
			return vt[1];
		}
	};

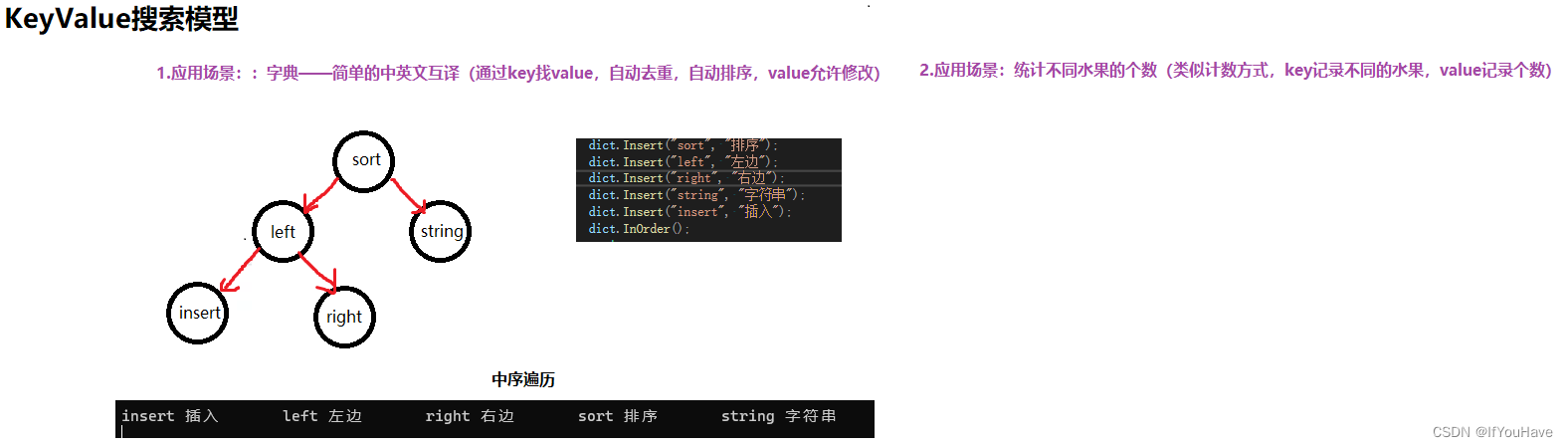
2. 二叉搜索树Key-Value模型及其应用

KV模型：每一个关键码key，都有与之对应的值Value，即的键值对。

 

该种方式在现实生活中非常常见： 比如英汉词典就是英文与中文的对应关系，通过英文可以快速找到与其对应的中文，英 文单词与其对应的中文就构成一种键值对； 再比如统计单词次数，统计成功后，给定单词就可快速找到其出现的次数，单词与其出 现次数就是就构成一种键值对。

template<class K,class V>
	class BSTreeNode {
	public:
		BSTreeNode(const K& key,const V& value)
			:_key(key)
			,_value(value)
			, _left(nullptr)
			, _right(nullptr)
		{
		}

		BSTreeNode<K,V>* _left;
		BSTreeNode<K,V>* _right;
		K _key;
		V _value;
	};
	//key
	template<class K, class V>
	class BinarySearchTree {
		typedef BSTreeNode<K,V> Node;

		void _destory(Node*& root) {
			if (root == nullptr) {
				return;
			}
			_destory(root->_left);
			_destory(root->_right);
			delete root;
			root = nullptr;
		}

		Node* _copy(Node* root) {
			if (root == nullptr) {
				return nullptr;
			}
			Node* copyRoot = new Node(root->_key);
			copyRoot->_left = _copy(root->_left);
			copyRoot->_right = _copy(root->_right);
			return copyRoot;
		}
	public:
		/*BinarySearchTree()
			:_root(nullptr)
		{

		}*/
		//拷贝构造也是构造，写了，编译器不在生成默认构造
		//强制编译器生成默认构造 —— c++11用法，default
		BinarySearchTree() = default;

		BinarySearchTree(const BinarySearchTree<K,V>& bst) {
			_root = _copy(bst._root);
		}
		~BinarySearchTree() {
			_destory(_root);
		}
		BinarySearchTree<K,V>& operator=(BinarySearchTree<K,V> bst) {
			std::swap(_root, bst._root);
			return *this;
		}

		bool Insert(const K& key,const V& value) {
			if (_root == nullptr) {
				_root = new Node(key,value);
				return true;
			}
			Node* cur = _root;
			Node* parent = nullptr;
			while (cur) {
				parent = cur;
				if (cur->_key > key) {
					cur = cur->_left;
				}
				else if (cur->_key < key) {
					cur = cur->_right;
				}
				else {
					return false;
				}
			}
			if (parent->_key > key) {
				parent->_left = new Node(key, value);
				return true;
			}
			else {
				parent->_right = new Node(key, value);
				return true;
			}
		}
		Node* Find(const K& key) const {
			if (_root == nullptr) {
				return nullptr;
			}
			Node* cur = _root;
			while (cur) {
				if (cur->_key > key) {
					cur = cur->_left;
				}
				else if (cur->_key < key) {
					cur = cur->_right;
				}
				else {
					return cur;
				}
			}
			return nullptr;
		}
		bool Erase(const K& key) {
			if (_root == nullptr) {
				return false;
			}
			Node* cur = _root;
			Node* parent = nullptr;
			while (cur) {
				if (cur->_key > key) {
					parent = cur;
					cur = cur->_left;
				}
				else if (cur->_key < key) {
					parent = cur;
					cur = cur->_right;
				}
				else {
					if (cur->_left == nullptr) {
						if (cur == _root) {
							_root = cur->_right;
						}
						else {
							if (cur == parent->_left) {
								parent->_left = cur->_right;
							}
							else {
								parent->_right = cur->_right;
							}
						}
						delete cur;
						cur = nullptr;
						return true;
					}
					else if (cur->_right == nullptr) {
						if (cur == _root) {
							_root = cur->_left;
						}
						else {
							if (cur == parent->_left) {
								parent->_left = cur->_left;
							}
							else {
								parent->_right = cur->_left;
							}
						}
						delete cur;
						cur = nullptr;
						return true;
					}
					else {
						//替换法删除 -- 右数最小节点
						Node* replace = cur->_right;
						Node* replaceParent = cur;
						while (replace->_left != nullptr) {
							replaceParent = replace;
							replace = replace->_left;
						}
						std::swap(cur->_key, replace->_key);
						if (replaceParent->_left == replace) {
							replaceParent->_left = replace->_right;
						}
						else {
							replaceParent->_right = replace->_right;
						}
						delete replace;
						return true;
					}
				}
			}
			return false;

		}
		void InOrder() {
			_InOrder(_root);
			cout << endl;
		}
	private:

		void _InOrder(Node* root) {
			if (root == nullptr) {
				return;
			}
			_InOrder(root->_left);
			cout << root->_key << " " << root->_value << "       ";
			_InOrder(root->_right);
		}
	private:
		Node* _root = nullptr;
	};

	void test() {
		BinarySearchTree<string, string> dict;
		dict.Insert("sort", "排序");
		dict.Insert("left", "左边");
		dict.Insert("right", "右边");
		dict.Insert("string", "字符串");
		dict.Insert("insert", "插入");
		dict.InOrder();
		string str;
		while (cin >> str) {
			BSTreeNode<string,string>* ret = dict.Find(str);
			if (ret != nullptr) {
				cout << "Find it :: " << str << "\t\tmean :: " << ret->_value << endl;
			}
			else {
				cout << "Not find it!!!" << endl;
			}
		}
		
	}

	void test1() {
		string arr[] = { "苹果", "苹果","香蕉","香蕉","梨" ,"西瓜","香蕉"};
		BinarySearchTree<string, int> statCount;
		int value = 0;
		for (auto& e : arr) {
			auto ret = statCount.Find(e);
			if (ret) {
				++ret->_value;
			}
			else {
				statCount.Insert(e, 1);
			}
		}
		statCount.InOrder();

	}

2、二叉树OJ

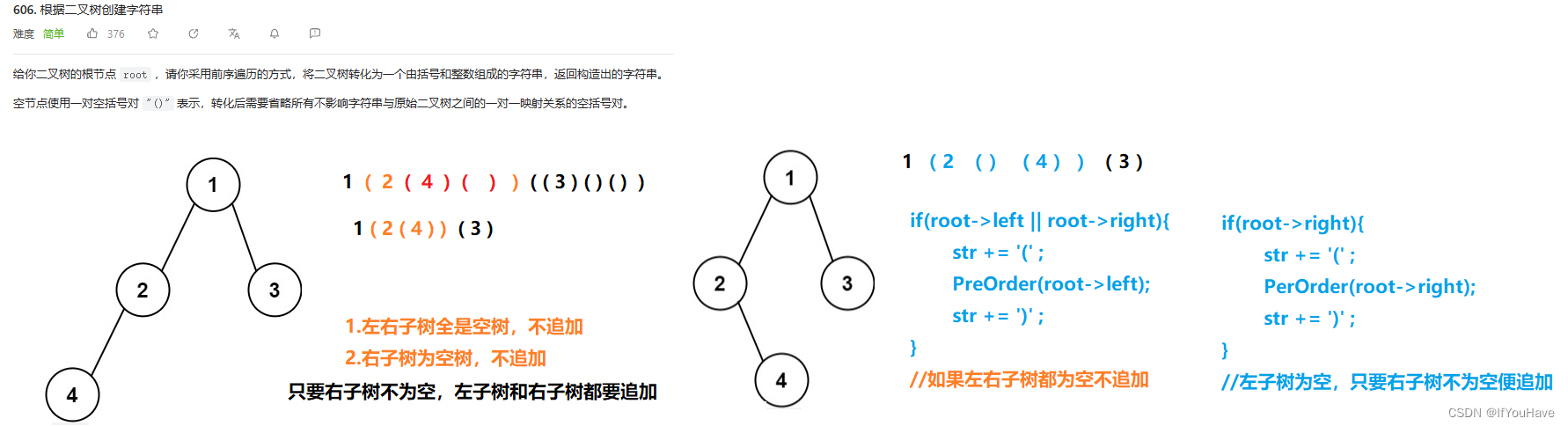
2.1 根据二叉树创建字符串

题目分析：

 代码：

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    void PerOrder(TreeNode* root,string& str){
        if(root == nullptr){
            return;
        }
        str += to_string(root->val);
       if(root->left || root->right){
           str += '(';
           PerOrder(root->left,str);
           str += ')';
       }
       if(root->right){
            str += '(';
            PerOrder(root->right,str);
            str += ')';
       }
    }
    string tree2str(TreeNode* root) {
        string str;
        PerOrder(root,str);
        return str;
    }
};

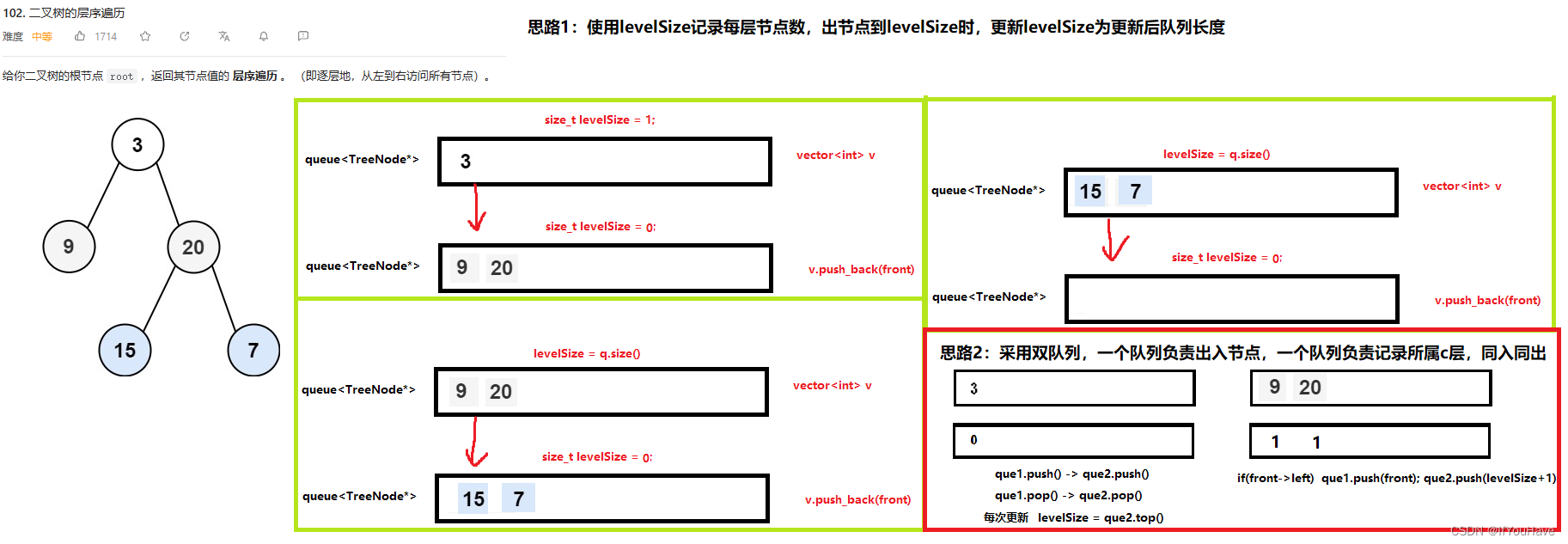
2.2 二叉树的层序遍历I

题目分析：

 思路一代码：

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    vector<vector<int>> levelOrder(TreeNode* root) {
        vector<vector<int>> vv;
        if (root == nullptr)
            return vv;
            
        queue<TreeNode*> q; 
        q.push(root);
        while (!q.empty())
        {
            vector<int> v;
            int sz = q.size();
            while (sz--)
            {
                TreeNode* front = q.front();
                v.push_back(front->val);
                q.pop();
                if (front->left) q.push(front->left);
                if (front->right) q.push(front->right);
            }
            vv.push_back(v);
        }
        return vv;
    }
};

思路二代码：

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    vector<vector<int>> levelOrder(TreeNode* root) {
        vector<vector<int>> vv;
        queue<TreeNode*> que1;
        queue<int> que2;
        size_t levelSize = 0;
        size_t newLevel = 0;
        if(root){
            que1.push(root);
            que2.push(levelSize);
        }
        vector<int> v;
        while(!que1.empty()){
            TreeNode* front = que1.front();que1.pop();// 15 17
            newLevel = que2.front();que2.pop();// 2 
            if(levelSize != newLevel){
                vv.push_back(v);
                v.clear();
                levelSize = newLevel;
            }
             v.push_back(front->val);// [3] [9,20]

            if(front->left){
                que1.push(front->left);// 15 17
                que2.push(newLevel + 1);// 2 2
            }
            if(front->right){
                que1.push(front->right);// 20
                que2.push(newLevel + 1);// 1
            }
        }
        if(!v.empty()){
            vv.push_back(v);
        }
        return vv;
    }
};

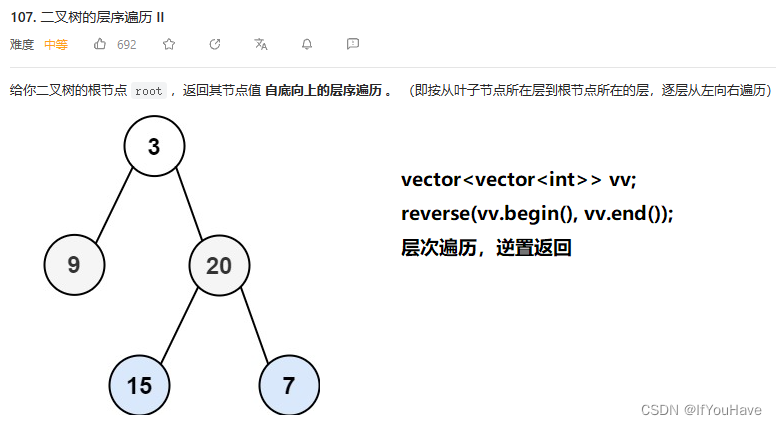
2.3 二叉树的层序遍历II

题目分析：

 代码：

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    vector<vector<int>> levelOrderBottom(TreeNode* root) {
        vector<vector<int>> vv;
        if (root == nullptr)
            return vv;
            
        queue<TreeNode*> q; 
        q.push(root);
        while (!q.empty())
        {
            vector<int> v;
            int sz = q.size();
            while (sz--)
            {
                TreeNode* front = q.front();
                v.push_back(front->val);
                q.pop();
                if (front->left) q.push(front->left);
                if (front->right) q.push(front->right);
            }
            vv.push_back(v);
        }
        reverse(vv.begin(),vv.end());
        return vv;
    }
};

2.4 二叉树的最近公共祖先

题目分析：

 

思路一使用Find代码：

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
 * };
 */
class Solution {
public:
    bool Find(TreeNode* root, TreeNode* x){
        if(root == nullptr){
            return false;
        }
        return root == x || Find(root->left,x) || Find(root->right,x);
    }
    TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
        if(root == nullptr){
            return nullptr;
        }
        if(root == p || root == q){
            return root;
        }
        bool pInLeft, pInRight, qInLeft, qInRight;
        pInLeft = Find(root->left, p);
        pInRight = !pInLeft;
        qInLeft = Find(root->left, q);
        qInRight = !qInLeft;
        if((pInLeft && qInRight) || (pInRight && qInLeft)){
            return root;
        }else if(pInLeft && qInLeft){ 
            return lowestCommonAncestor(root->left, p,  q);
        }else{
            return lowestCommonAncestor(root->right, p,  q);
        }
        
    }
};

思路二使用FindWay代码：

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
 * };
 */
class Solution {
public:
    bool FindWay(TreeNode* root, TreeNode* x, stack<TreeNode*>& st){
        if(root == nullptr){
            return false;
        }
        st.push(root);
        if(root == x){
            return true;
        }
        if(FindWay(root->left, x, st)){
            return true;
        }
        if(FindWay(root->right, x, st)){
            return true;
        }
        st.pop();
        return false;
    }
    TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
        stack<TreeNode*> pPath;
        stack<TreeNode*> qPath;
        FindWay(root, p, pPath);
        FindWay(root, q, qPath);
        while(pPath.size() != qPath.size()){
            if(pPath.size() > qPath.size()){
                pPath.pop();
            }
            else{
                qPath.pop();
            }
        }
        while(pPath.top() != qPath.top()){
            pPath.pop();
            qPath.pop();
        }
        return pPath.top();
    }
};

2.5 二叉搜索树及双向链表

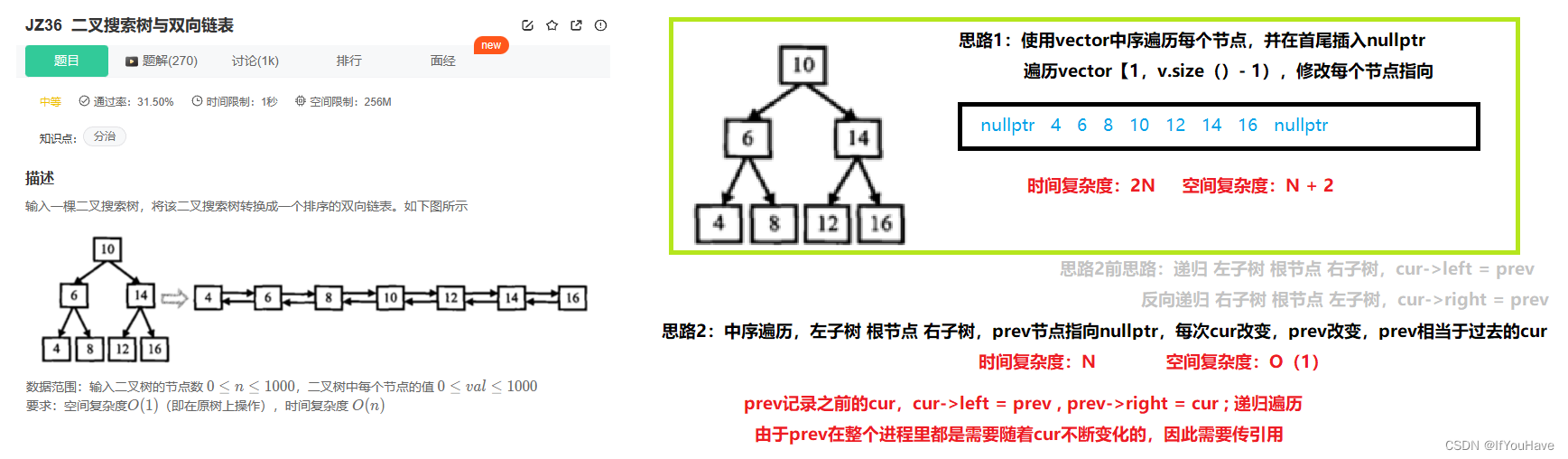
题目分析：

 

思路一代码：

/*
struct TreeNode {
	int val;
	struct TreeNode *left;
	struct TreeNode *right;
	TreeNode(int x) :
			val(x), left(NULL), right(NULL) {
	}
};*/
/*
#include <vector>
class Solution {
public:
	void InOrder(TreeNode* root,vector<TreeNode*>& vt){
		if(root == nullptr){
			return;
		}
		InOrder(root->left,vt);
		vt.push_back(root);
		InOrder(root->right,vt);
	}
    TreeNode* Convert(TreeNode* pRootOfTree) {
        vector<TreeNode*> vt;
		vt.push_back(nullptr);
		InOrder(pRootOfTree,vt);
		vt.push_back(nullptr);
		for(size_t i = 1; i < vt.size() - 1; ++i){
				vt[i]->left = vt[i-1];
				vt[i]->right = vt[i+1];
		}
		return vt[1];
    }
};

思路二代码：

/*
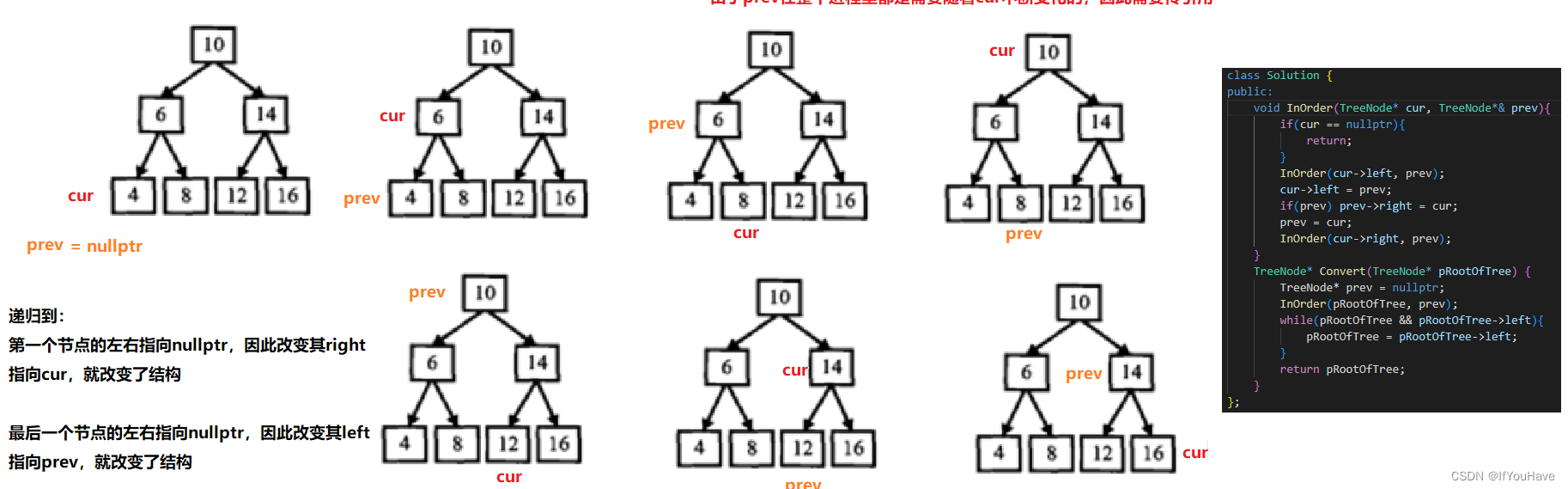
struct TreeNode {
	int val;
	struct TreeNode *left;
	struct TreeNode *right;
	TreeNode(int x) :
			val(x), left(NULL), right(NULL) {
	}
};*/

#include <vector>
class Solution {
public:
	void InOrder(TreeNode* cur,TreeNode*& prev){
		if(cur == nullptr){
			return;
		}
		InOrder(cur->left,prev);
		cur->left = prev;
		if(prev) prev->right = cur;
		prev = cur;
		InOrder(cur->right,prev);
	}
    TreeNode* Convert(TreeNode* pRootOfTree) {
        TreeNode* prev = nullptr;
		InOrder(pRootOfTree, prev);
		while(pRootOfTree && pRootOfTree->left){
			pRootOfTree = pRootOfTree->left;
		}
		return pRootOfTree;
    }
};

2.6 从前序与中序遍历序列构造二叉树

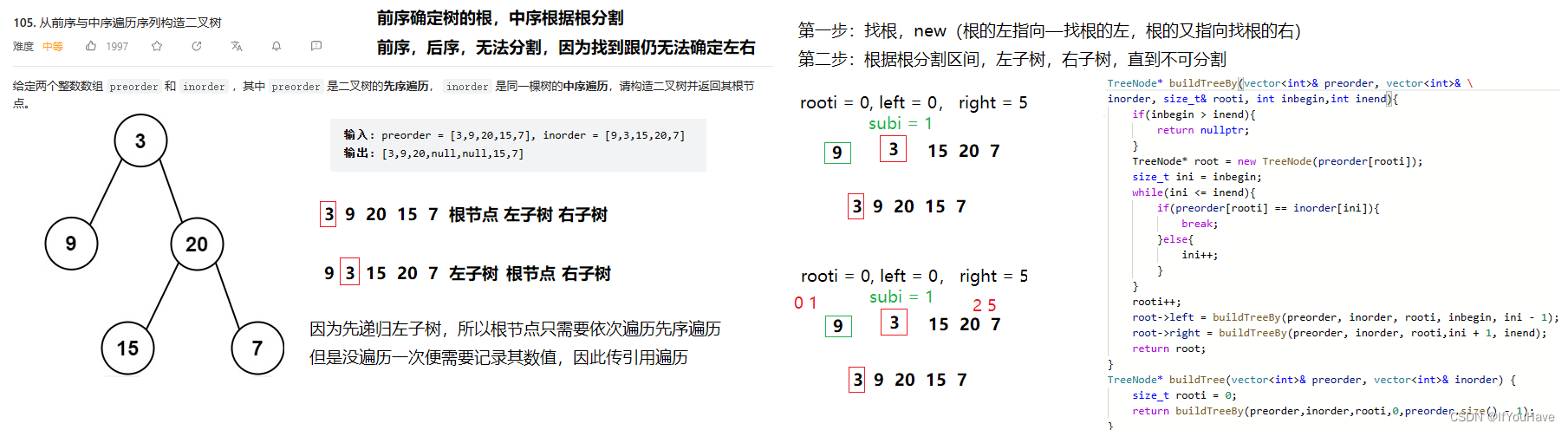
题目分析：

 

代码：

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    TreeNode* buildTreeBy(vector<int>& preorder, vector<int>& inorder, size_t& rooti, int inbegin,int inend){
        if(inbegin > inend){
            return nullptr;
        }
        TreeNode* root = new TreeNode(preorder[rooti]);
        size_t ini = inbegin;
        while(ini <= inend){
            if(preorder[rooti] == inorder[ini]){
                break;
            }else{
                ini++;
            }
        }
        rooti++;
        root->left = buildTreeBy(preorder, inorder, rooti, inbegin, ini - 1);
        root->right = buildTreeBy(preorder, inorder, rooti,ini + 1, inend);
        return root;
    }
    TreeNode* buildTree(vector<int>& preorder, vector<int>& inorder) {
        size_t rooti = 0;
        return buildTreeBy(preorder,inorder,rooti,0,preorder.size() - 1);
    }
};

2.7 从中序与后序遍历序列构造二叉树

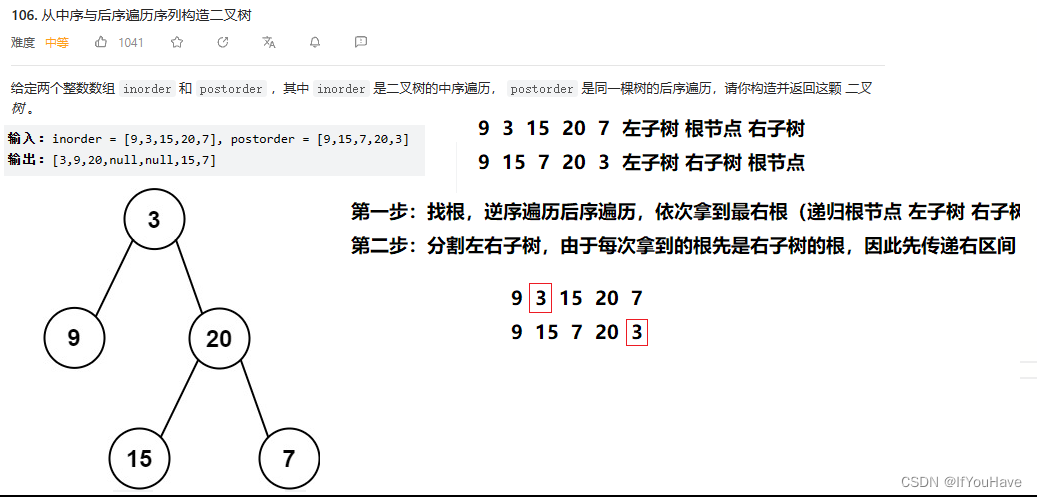
题目分析：

 

代码：

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    TreeNode* buildTreeBy(vector<int>& inorder, vector<int>& postorder, size_t& rooti, int inbegin, int inend){
        if(inbegin > inend){
            return nullptr;
        }
        TreeNode* root = new TreeNode(postorder[rooti--]);
        int ini = inbegin;
        while(ini <= inend){
            if(inorder[ini] == root->val){
                break;
            }
            ++ini;
        }
        root->right = buildTreeBy(inorder,postorder,rooti,ini + 1,inend);
        root->left = buildTreeBy(inorder,postorder,rooti,inbegin,ini-1);
        return root;
    }
    TreeNode* buildTree(vector<int>& inorder, vector<int>& postorder) {
        size_t rooti = postorder.size() - 1;
        return buildTreeBy(inorder,postorder,rooti,0,inorder.size() - 1);
    }
};

3、非递归实现二叉树遍历

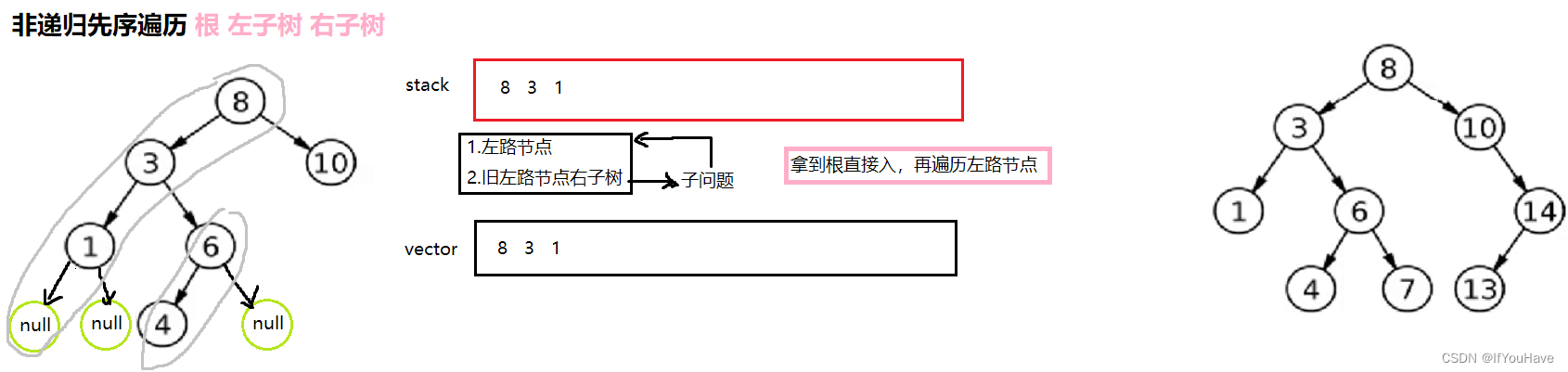
3.1 非递归前序遍历

图解分析：

 代码：

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
 #include<vector>
class Solution {
public:
    vector<int> preorderTraversal(TreeNode* root) {
        vector<int> v;
        stack<TreeNode*> st;
        TreeNode* cur = root;
        while(cur || !st.empty()){
            //左路节点
            while(cur){
                v.push_back(cur->val);
                st.push(cur);
                cur = cur->left;
            }
            //重置左路节点，为其原左路节点的右子树
            cur = st.top();
            st.pop();
            cur = cur->right;
        }
        return v;
    }
};

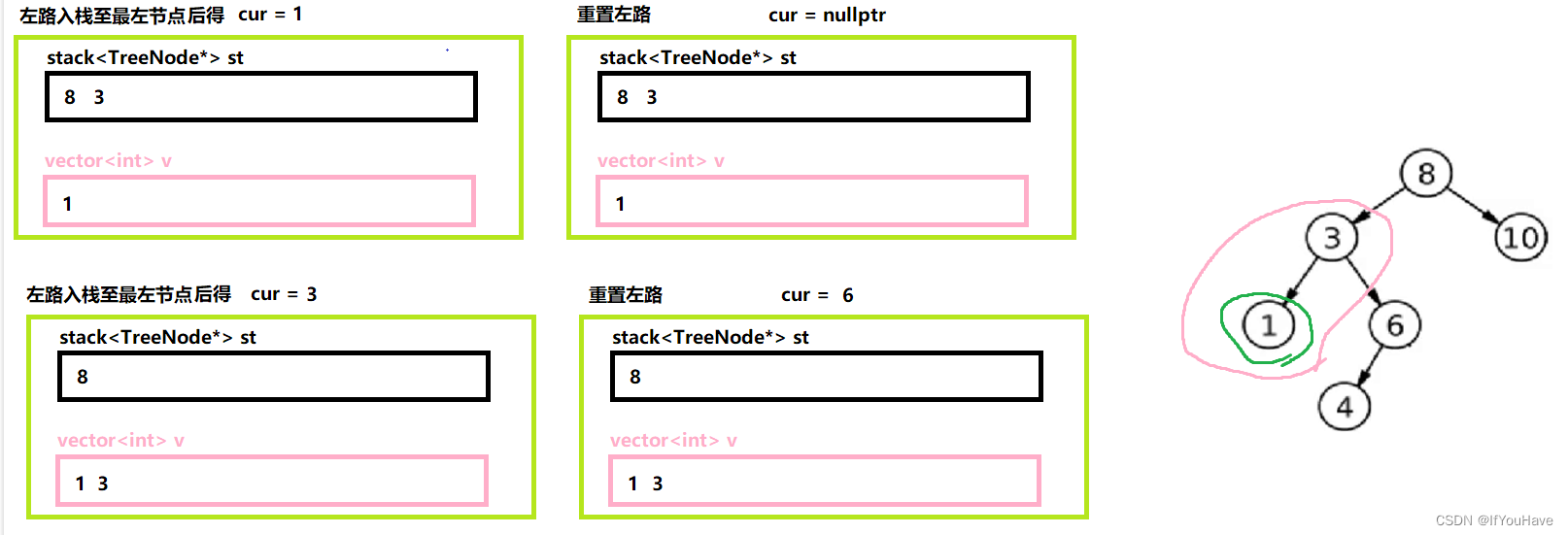
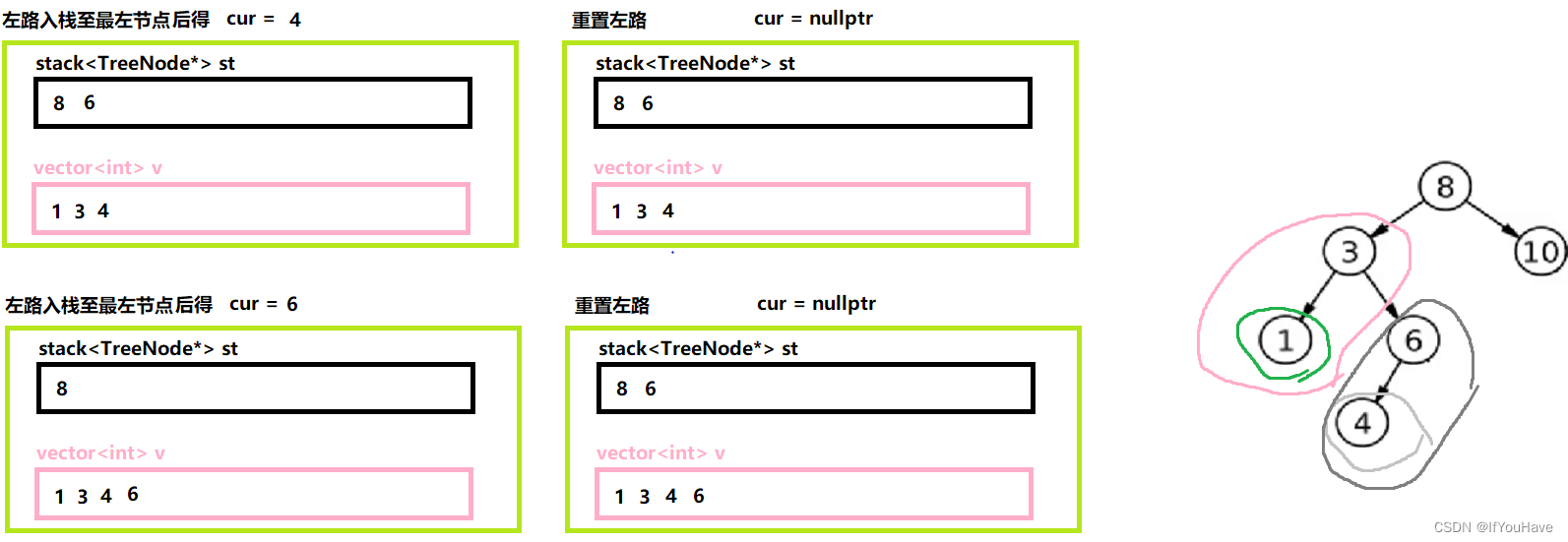
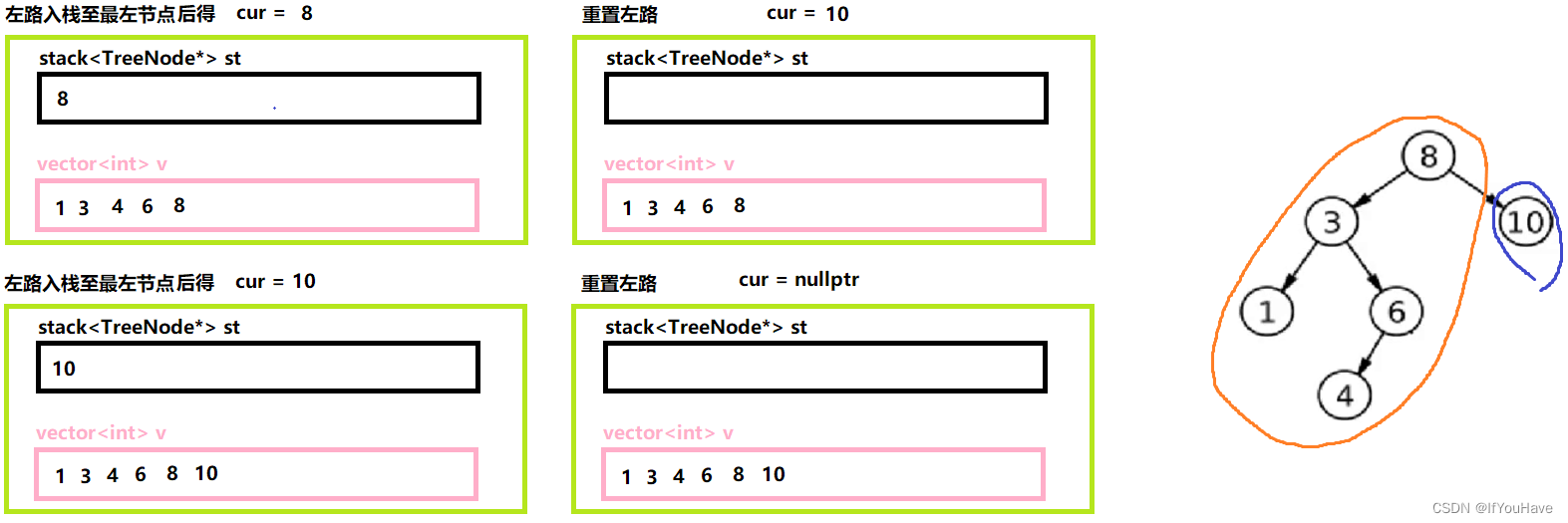
3.2 非递归实现中序遍历

图解分析：

代码：

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    vector<int> inorderTraversal(TreeNode* root) {
        vector<int> v;
        stack<TreeNode*> st;
        TreeNode* cur = root;
        while(cur || !st.empty()){
            while(cur){
                st.push(cur);
                cur = cur->left;
            }
            cur = st.top();
            st.pop();
            v.push_back(cur->val);
            cur = cur->right;
        }
        return v;
    }
};

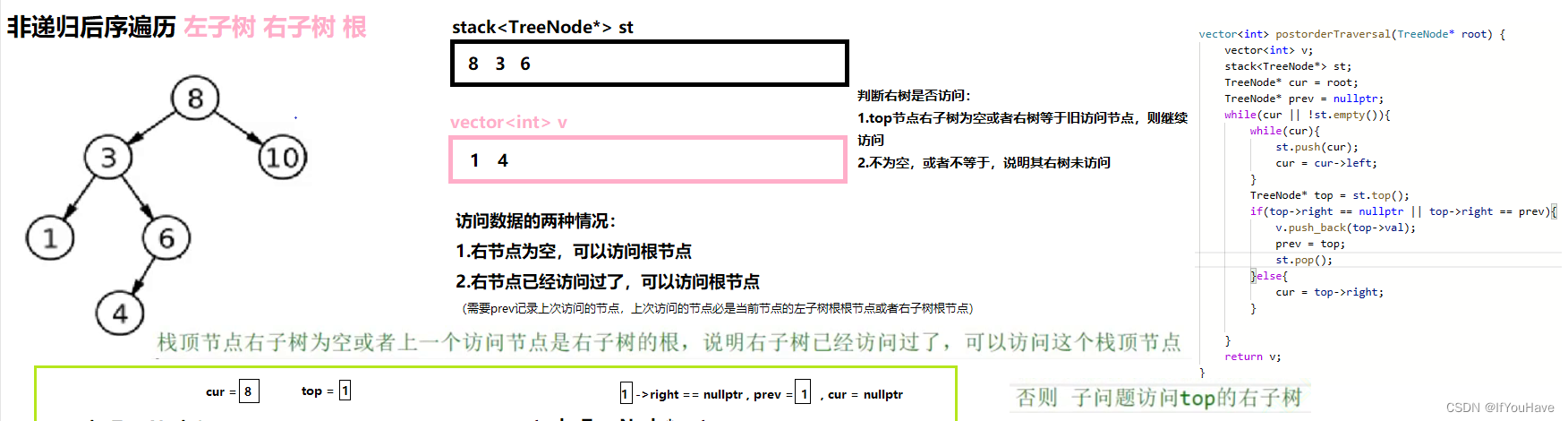
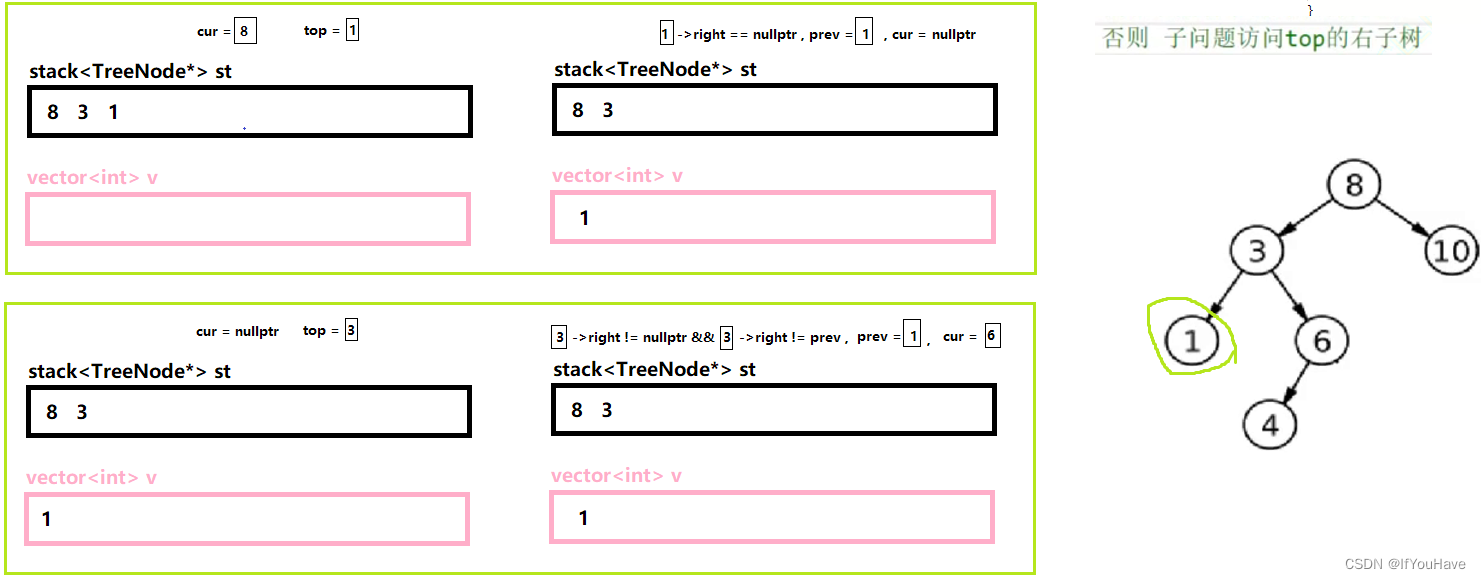
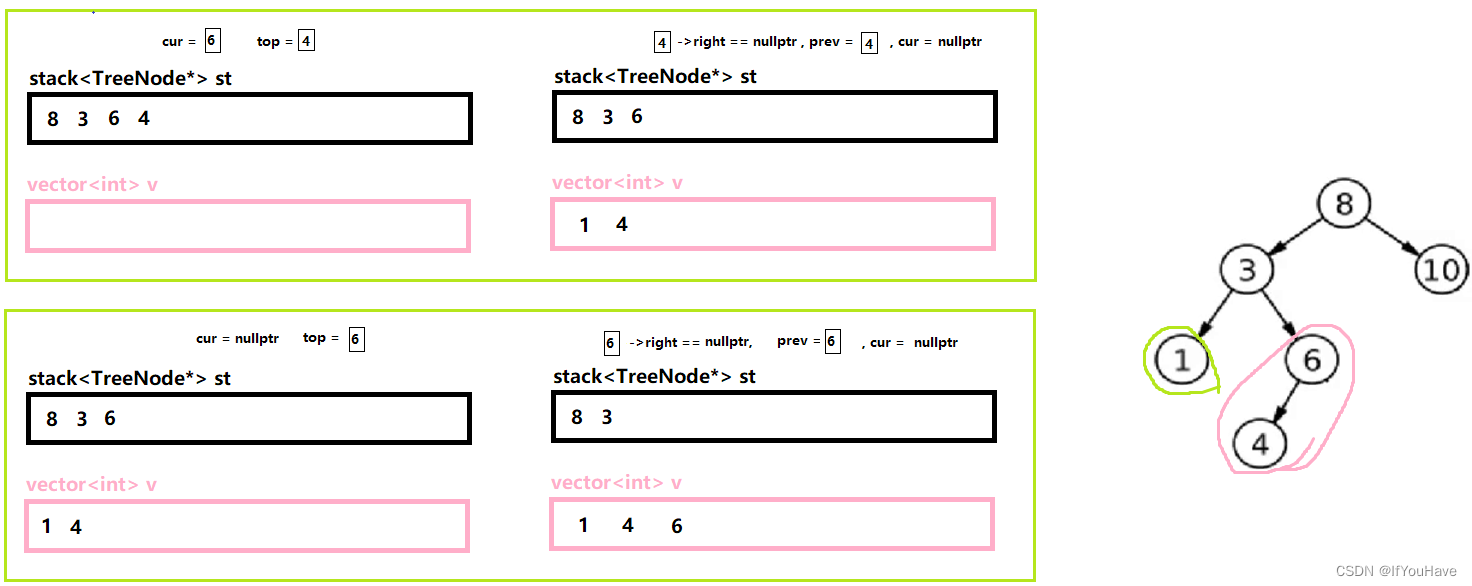
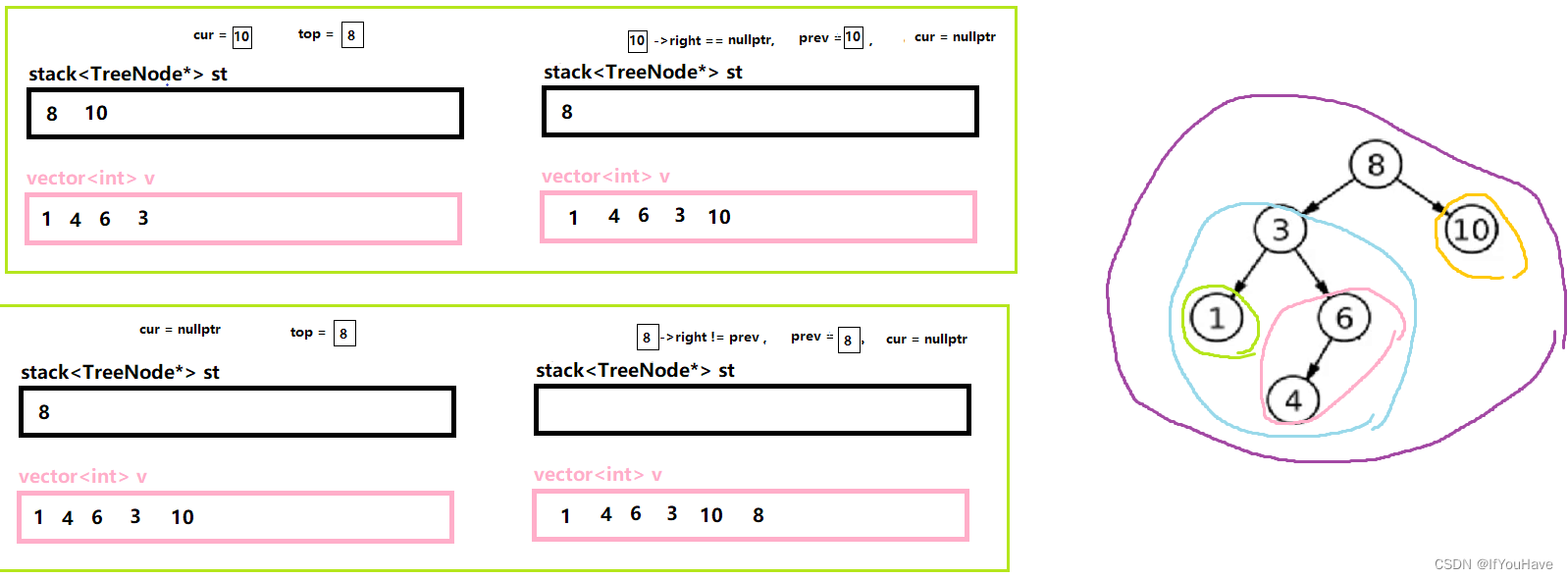
3.3 非递归实现后序遍历

图解分析：

 

代码：

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    vector<int> postorderTraversal(TreeNode* root) {
        vector<int> v;
        stack<TreeNode*> st;
        TreeNode* cur = root;
        TreeNode* prev = nullptr;
        while(cur || !st.empty()){
            while(cur){
                st.push(cur);
                cur = cur->left;
            }
            TreeNode* top = st.top();
            if(top->right == nullptr || top->right == prev){
                v.push_back(top->val);
                prev = top;
                st.pop();
            }else{
                cur = top->right;
            }

        }
        return v;
    }
};

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/691748.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

想学芯片专业？一文讲清楚芯片报考指南

想学芯片专业？一文讲清楚芯片报考指南

2021年清北相继成立集成电路学院之后&#xff0c;国内在电子方面有实力积累的高校纷纷跟进&#xff0c;设立集成电路学院、开设集成电路相关专业。 直到今年&#xff0c;高校在集成电路方面的投入和培养力度&#xff0c;仍在持续并越来越大。 就在今年&#xff0c;示范性28所…
阅读更多...
CDN是什么？

CDN是什么？

81. CDN是什么&#xff1f; CDN&#xff08;Content Delivery Network&#xff09; 即内容分发网络&#xff0c;是一种分布式的网络架构&#xff0c;旨在提高用户获取内容的速度、可用性和安全性。CDN通过将内容部署到全球各个节点服务器&#xff0c;并根据用户的地理位置将内…
阅读更多...
有关软件检测实验室检测报告的全部知识点盘点

有关软件检测实验室检测报告的全部知识点盘点

检测报告是实验室检测成果的重要载体&#xff0c;也是软件检测实验室质量管理水平的一个重要体现&#xff0c;本文我们就一起来看一下&#xff0c;软件检测实验室在申请cnas测试认证时&#xff0c;应该如何规范实验室的检测报告。 首先我们一起来看一下&#xff0c;cnas官方对…
阅读更多...
记编译 Doris 的过程

记编译 Doris 的过程

目录 概述 1、关于clang 2、链接静态库的问题 3、 cmake的知识 4、关于nm 5、关于 ABI 6、关于debug info 概述 尝试编译 doris&#xff0c;其过程异常坎坷&#xff0c;不过也学到了很多东西。 首先&#xff0c;按照doris官网上的编译指导&#xff0c;下载ldb_toolchai…
阅读更多...
python图像处理实战（三）—图像几何变换

python图像处理实战（三）—图像几何变换

&#x1f680;写在前面&#x1f680; &#x1f58a;个人主页&#xff1a;https://blog.csdn.net/m0_52051577?typeblog &#x1f381;欢迎各位大佬支持点赞收藏&#xff0c;三连必回&#xff01;&#xff01; &#x1f508;本人新开系列专栏—python图像处理 ❀愿每一个骤雨初…
阅读更多...
Vue实例知识点分享

Vue实例知识点分享

文章目录 导文下面是创建 Vue 实例的基本步骤 常用的 Vue 实例方法和属性总结 导文 Vue的实例是用来创建 Vue 应用程序的对象。通过实例化 Vue 构造函数&#xff0c;我们可以创建一个具有响应式数据、计算属性、方法和生命周期钩子等特性的 Vue 实例。 下面是创建 Vue 实例的基…
阅读更多...
springDatajpa动态sql根据时间范围将数据导出为excel并使用vue的按钮去触发

springDatajpa动态sql根据时间范围将数据导出为excel并使用vue的按钮去触发

用到的技术点&#xff1a; 1.springDatajpa 2.EasyExcel 3.数据库 4.vue 前端实现&#xff1a; 1.创建按钮&#xff08;点击此按钮弹出填写导出条件的弹出框&#xff09; <el-button type"primary" round click"dialogVisible true"><svg-icon …
阅读更多...
Java如何实现分库分表

Java如何实现分库分表

一、为啥要分库分表 在大型互联网系统中&#xff0c;大部分都会选择mysql作为业务数据存储。一般来说&#xff0c;mysql单表行数超过500万行或者单表容量超过2GB&#xff0c;查询效率就会随着数据量的增长而下降。这个时候&#xff0c;就需要对表进行拆分。 那么应该怎么拆分…
阅读更多...
vite项目中处理各种静态资源的引入方式介绍

vite项目中处理各种静态资源的引入方式介绍

一、引用图片资源 在vite创建的vue3项目中&#xff0c;引用图片资源有以下两种方式&#xff1a; 直接在模板中使用路径引用&#xff1a;在模板中使用标签&#xff0c;通过src属性引用图片。例如&#xff1a; <template><div><img src"./assets/logo.png…
阅读更多...
NetApp FAS 存储管理软件，海量非结构化数据存储

NetApp FAS 存储管理软件，海量非结构化数据存储

NetApp FAS 存储管理软件&#xff0c;海量非结构化数据存储 在 NetApp ONTAP 数据管理软件的支持下&#xff0c;帮助您构建简单、安全且值得信赖的存储基础架构。NetApp FAS 存储阵列可让客户同时兼顾性能和容量。 NetApp FAS 系统经过优化&#xff0c;易于部署和操作&#x…
阅读更多...
记录ip段解析成ip

记录ip段解析成ip

无脑记录者记录使用方法 1.源代码链接 https://github.com/codeexpress/cidr2ip 2.提前准备的内容 go开发语言&#xff0c;链接里面的main.go 3.使用方法 直接新增文件cidrs.txt cidrs.txt文件里面加入需要解析的ip段即可
阅读更多...
【实战】 JWT、用户认证与异步请求(上) —— React17+React Hook+TS4 最佳实践，仿 Jira 企业级项目（四）

【实战】 JWT、用户认证与异步请求(上) —— React17+React Hook+TS4 最佳实践，仿 Jira 企业级项目（四）

文章目录 一、项目起航&#xff1a;项目初始化与配置二、React 与 Hook 应用&#xff1a;实现项目列表三、TS 应用&#xff1a;JS神助攻 - 强类型四、JWT、用户认证与异步请求1.login2.middleware of json-server3.jira-dev-tool&#xff08;imooc-jira-tool&#xff09;安装问…
阅读更多...
机器学习——自然语言处理（一）

机器学习——自然语言处理（一）

1 分词 1.1 设计原则 切分粒度大&#xff1b;非字典词少、单字字典词少&#xff1b;总体次数少。 1.2 基于词典匹配的分词 1.3 基于语法和规则的分词 目前处在试验阶段 1.4 基于统计的分词 1.5 技术难点 1.5.1 歧义识别 交集型歧义&#xff1a;AB | C or A | BC 组合型…
阅读更多...
Jmeter操作数据库运行提示“Cannot load JDBC driver class ‘com.mysql.jdbc.Driver‘”的有效解决

Jmeter操作数据库运行提示“Cannot load JDBC driver class ‘com.mysql.jdbc.Driver‘”的有效解决

如图所示&#xff0c;在jmeter中运行sql时报错提示“Cannot load JDBC driver class com.mysql.jdbc.Driver” 原因分析&#xff1a;这是因为没有mysql驱动&#xff0c;需要下载对应的jar包 一、下载地址&#xff1a;MySQL :: Download Connector/J 根据需求选择下载&#xf…
阅读更多...
数字化转型：智慧物业行业落地与应用的突围之路！

数字化转型：智慧物业行业落地与应用的突围之路！

导语 | 红杉中国在《2021 年企业数字化年度指南》中指出&#xff0c;96% 的受访企业已经开展了数字化实践&#xff0c;而其中超过 6 成的受访者都表示期望在未来进一步增加数字化的投入。技术因素或将成为未来两到三年影响企业发展最为重要的外部力量。当前地产与物业行业进入不…
阅读更多...
当前最强的免费AI画图、AI绘图工具-2

当前最强的免费AI画图、AI绘图工具-2

Midjourney比较贵&#xff0c;而且无法访问&#xff0c;Stable Diffusion部署起来很麻烦。网上有哪些可以直接在网页端或者下载的app可以实现AI画图的工具。我们整理了45个相关工具&#xff0c;这是系列2&#xff0c;收录到 当前最强的免费AI画图、AI绘图工具-2https://www.web…
阅读更多...
【C++】-- 高并发内存池

【C++】-- 高并发内存池

高并发内存池 项目介绍池化技术内存池 定长内存池的实现整体框架threadcachethreadcache整体设计threadcache哈希桶映射对齐规则TLS无锁访问 centralcachecentralcache整体设计centralcache结构设计centralcache的实现 pagecachepagecache整体设计pagecache中获取Span 回收内存…
阅读更多...
【C/C++练习】经典的快慢指针问题---移除元素

【C/C++练习】经典的快慢指针问题---移除元素

&#x1f4d6;题目描述 题目出处&#xff1a;移除元素 &#x1f516;示例 &#x1f4d6;题解 对于本题我将按照由易到难的顺序为大家分享三种解题思路&#xff0c;并逐一分析它们的优劣&#xff0c;以及注意事项。 &#x1f516;思路一&#xff1a;暴力求解 我想暴力求解应该…
阅读更多...
零-云尚办公项目学习

零-云尚办公项目学习

对于云尚办公项目的学习 1、这是尚硅谷推出的新的OA项目 云尚办公系统是一套自动办公系统&#xff0c;系统主要包含&#xff1a;管理端和员工端 管理端包含:权限管理、审批管理、公众号菜单管理 员工端:采用微信公众号操作&#xff0c;包含&#xff1a;办公审批、微信授权登…
阅读更多...
数字通信中的编码（学习笔记）

数字通信中的编码（学习笔记）

编码种类 RZ(Return Zero Code)编码 也称为归零码&#xff0c;就是在 一个周期内&#xff0c;用二进制传输数据位&#xff0c;在数据脉冲结束后&#xff0c;需要维持一段时间的低电平。 RZ编码又分为两种&#xff1a; 单极性归零码 低电平表示0&#xff0c;正电平表示1&…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023