| 一、实验目的: 1. 练习建立实际问题的多目标规划模型。 2. 掌握用数学软件求解多目标规划的方法。 3. 实验从算法思想、实验步骤与程序、运行结果、结果分析与讨论等几方面完成。 4. 预习多目标规划的理论内容。 | ||||||||
| 二、实验内容
第一目标:充分利用正常的生产能力,避免开工不足. 第二目标:优先满足老客户的需求,A,B,C这3种型号的电脑50,50,80(台),同时根据3种电脑的纯利润分配不同的权因子. 第三目标:限制装配线加班时间,不允许超过200h. 第四目标:满足各种型号电脑的销售目标,A,B,C型号分别为100,120,100(台),再根据3种电脑的纯利润分配不同的权因子. 第五目标:装配线的加班时间尽可能少. 数学模型:
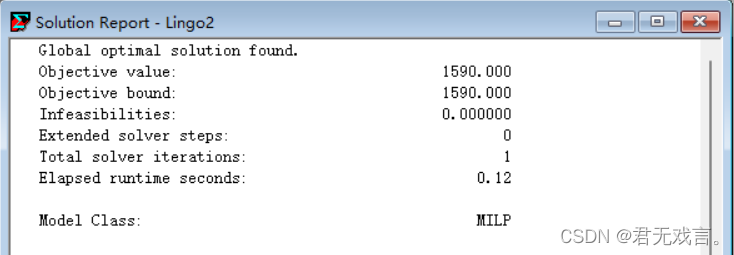
程序代码: model: sets: vable/1..3/:x; num/1..8/:g,a,b; yueshu(num,vable):c; endsets data: g=1700 50 50 80 100 120 100 1900; c=5 8 12 1 0 0 0 1 0 0 0 1 1 0 0 0 1 0 0 0 1 5 8 12; enddata min=20*b(5)+18*b(6)+21*b(7); @for(num(i):@sum(vable(j):c(i,j)*x(j))+b(i)-a(i)=g(i)); b(1)=0; 20*b(2)+18*b(3)+21*b(4)=0; a(8)=0; @for(vable:@gin(x)); end 程序执行结果:
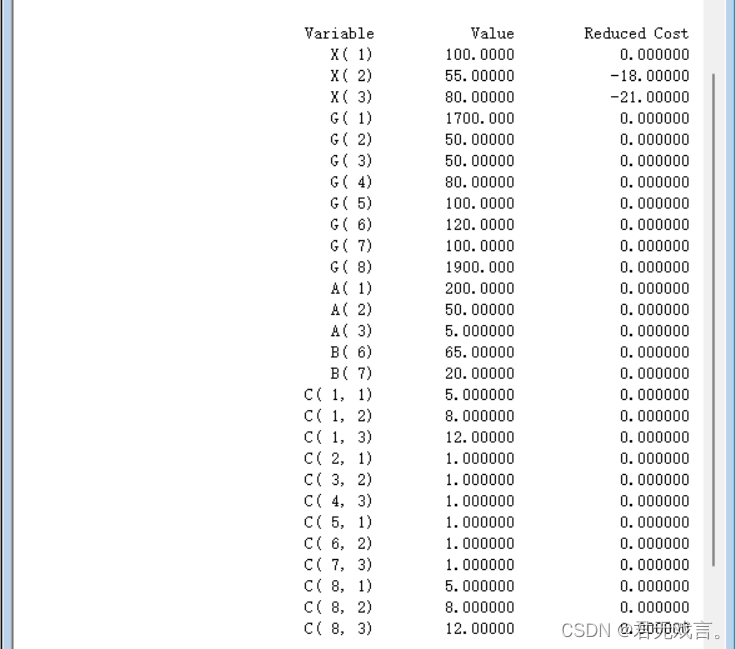
结果解释: 由运行结果可知,x1=100,x2=55,x3=80,装配线生产时间为1900小时,满足装配线加班不超过 200小时的要求。能够满足老客户的需求,但未能达到销售目标。销售总利润为﹐100*1000+55*1440+80*2520=380800(元)。
试问工厂如何安排生产计划,在满足市场需要的前提下,使设备投资和公害损失均达最小。该工厂决策认为,这两个目标中环境污染应优先考虑,设备投资的目标值为20万元,公害损失的目标为12万元。 数学模型:环境污染优先考虑则将环境污染值权重赋
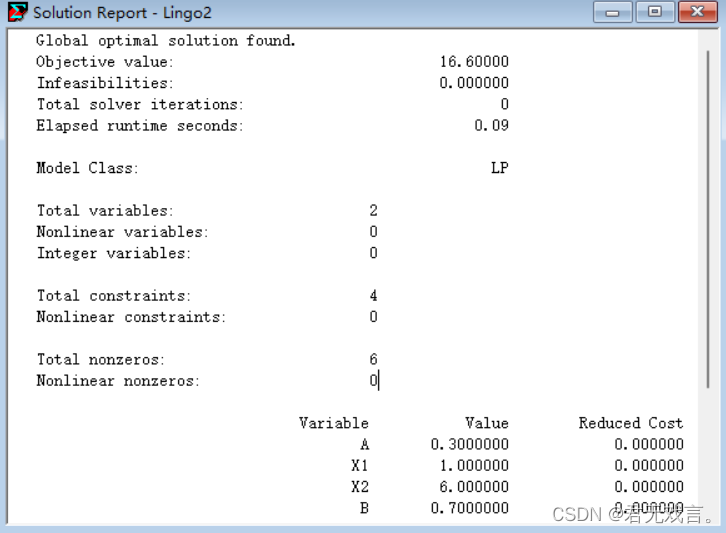
程序代码: model: min=a*(2*x1+5*x2)+b*(4*x1+x2); data: a=0.3; b=0.7; enddata x1<5; x2<6; x1+x2>7; end 程序执行结果:
结果解释: 得到x1=1,x2=6,满足总产量不少于7吨的要求,且均在生产能力范围内。此时所得收益为1*2+6*5=32万元/吨,到达了目标值,所造成的公害损失为1*4+6*1=10万元/吨,未超过目标值。 | ||||||||
| 分析与讨论: 1.描述线性目标规划的单纯形法算法过程? 具体算法过程如下:
- 最大化目标函数,即将目标函数的系数取相反数 - 所有约束条件转化为等式形式,引入人工变量和松弛变量 - 将约束条件与目标函数写成矩阵形式
- 以目标函数系数中最大的负数作为进入变量 - 以系数矩阵中最小非零元所在的行作为出去变量 - 对所有与出去变量有关的元素作初等行变换,使得出去变量成为单位向量 - 重复以上步骤,直到找到最优解或确定问题无解
- 在单纯形中选择离最优解最近的角点作为新的初始单纯形 - 逐步调整单纯形以找到更优的角点 - 重复以上步骤直到找到最优解
- 如果目标函数的最大值/最小值等于0,则原问题有解且最优解为0 - 如果目标函数的最大值/最小值大于0/小于0,则原问题有/无解 |
最优化方法(基于lingo)之 目标规划问题求解(6/6)
news2026/2/12 17:34:30
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如若转载,请注明出处:http://www.coloradmin.cn/o/691166.html
如若内容造成侵权/违法违规/事实不符,请联系多彩编程网进行投诉反馈,一经查实,立即删除!相关文章
一篇文章告诉你,全网爆款抓包工具的优劣势
前言
作为软件测试工程师,抓包总是不可避免:遇到问题要做分析需要抓包;发现 bug 需要定位要抓包;检查数据传输的安全性需要抓包;接口测试遇到需求不全的也需要抓包... 就因为抓包在测试工作中无处不在,所以…
TuyaOS 开发固件OTA配置指南
文章目录 一、固件升级配置升级信息设置配置中英文升级文案配置发布范围固件升级验证 二、固件升级发布 通过TuyaOS接入涂鸦云的产品全部默认支持固件OTA功能,TuyaOS设备实现固件OTA需要: 自定义产品创建TuyaOS嵌入式开发固件上传固件OTA配置与发布
等步…
PMP知识点汇总完善版,2023年8月考试就靠它了
第1章 整体管理 1.1 制定项目章程
是制定一份正式批准项目或阶段的文件,并记录能反应干系人需要和期望的初步要求的过程。由项目以外的人员批准,如发起人,批准标志项目的正式启动。 1.1.1 知识点汇总
1、由项目以外的人员批准,如…
Mac iterm Ctrl + V内容前后出现了0~ 1~
背景
笔者周六日加班的时候,被小外甥看到,小外甥就对电脑玩了起来,玩完就这样了
现象
iterm2中复制黏贴出现如下现象:
解决
经过了解是启用了括号粘贴,不得不感叹两岁小外甥这天赋真逆天啊,不辜负他爸…
深入浅出设计模式 - 抽象工厂模式
博主介绍: ✌博主从事应用安全和大数据领域,有8年研发经验,5年面试官经验,Java技术专家✌ Java知识图谱点击链接:体系化学习Java(Java面试专题) 💕💕 感兴趣的同学可以收…
自动化测试框架[Cypress概述]
目录
前言:
Cypress简介
Cypress原理
Cypress架构图
Cypress特性
各类自动化测试框架介绍 Selenium/WebDriver
Karma
Karma的工作流程
Nightwatch
Protractor
TestCafe
Puppeteer 前言:
Cypress是一个基于JavaScript的端到端自动化测试框架…
个人自我评价格式范文五篇
★个人自我评价1 工作已经进行两周多了,突然发现自己似乎又重蹈覆辙了,再一次一次的不经意中和某些人的就距离却是越来越来大,总是想偷一下懒,总是想着马马虎虎过去算了,没有那么精打细算过。结果不经意有些人人开始脱…
android的项目下的res文件夹下的部分文件夹介绍
1.看图 drawable文件夹下的图片是不压缩的图片 drawable-xhdpi文件夹下的图片是适合指定分辨率的图片 mipmap-xxhdpi文件夹下的图片是小型设备分辨率的图片
基于物联网、云计算建设的智慧校园云平台源码
电子班牌作为班级文化展示交流的窗口,可以让更多的人看到校园信息建设与班级风格相结合,及时传递校园信息。学生也可以通过电子班牌看到学校近期重要事件的发布,也可以参与回复,让学生及时掌握校园和班级动态。同时,还…
版本管理可视化工具GitKraKe安装
资源下载地址 https://download.csdn.net/download/u012796085/87953404
1 解压后安装GitKrakenSetup-7.5.5.exe
2 命令窗口进入GitKraken存放目录,分别执行以下语句
git clone https://gitee.com/pan13640612207/GitKraken.git
cd GitKraken/
yarn install
yarn…
STM32使用STM32CUBEMX配置FreeRTOS+SDIO4bit+FATFS注意事项
一、使用STM32CUBEMX配置FreeRTOSSDIO4bitFATFS注意事项:
以STM32F429为例: 1、SDIO配置 配置为4bit模式,此配置不是最终配置,后面会在代码进行修改。 2、Fatfs配置 Set Defines 选项中的配置可以默认,最重要注意Ad…
git配置和git合并
git配置:
首先下载安装git:https://git-scm.com/downloads/
一路默认,安装完成后,打开文件夹C:\Users\Administrator\.ssh(Administrator是当前用户名),在空白处点鼠标右键选择“Git Bush Her…
和鲸助力中国大学生计算机设计大赛国赛作品评审标准落实研讨会召开,专家平台首发布
6月16日至19日,中国大学生计算机设计大赛国赛作品评审标准落实研讨会(第一期)在天津召开,本次会议由中国大学生计算机设计大赛组委会主办,南开大学承办,和鲸社区参与协办。
会议由中国人民大学杜小勇教授、…
GPIO模拟时序控制外设1——WS2812B
文章目录 前言WS2812B1.模块简介2.时序介绍3.硬件介绍4.传输速率,以及帧数要求 代码1.初始化2.模拟时序1.复位函数2.发送0、1码3.封装发送函数 总结 前言
上一篇文章中介绍了整个板子的最基本功能模块——使用GPIO的通用输入输出实现简单的按键输入以及推挽输出控制…
【若依分离版操作方法日志与其它业务数据(如入库操作)关联的实现】
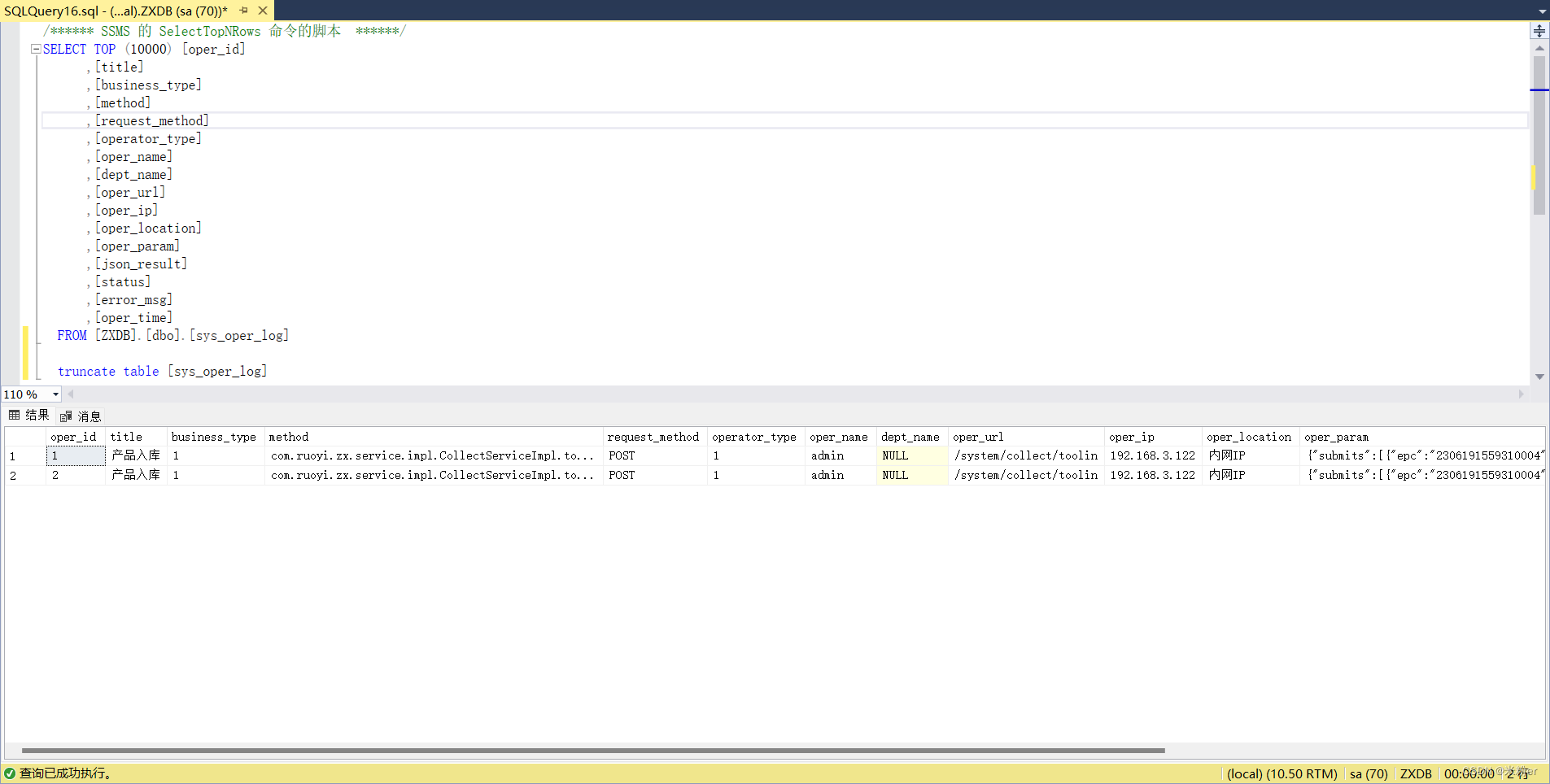
若依框架业务表和操作日志表关联 需求:分析:思路:实现: 需求:
基于若依分离版框架业务数据与操作日志的数据做个关联 入库表 /*入库业务表 */
CREATE TABLE [BS_In]( [Id] int IDENTITY(1,1)…
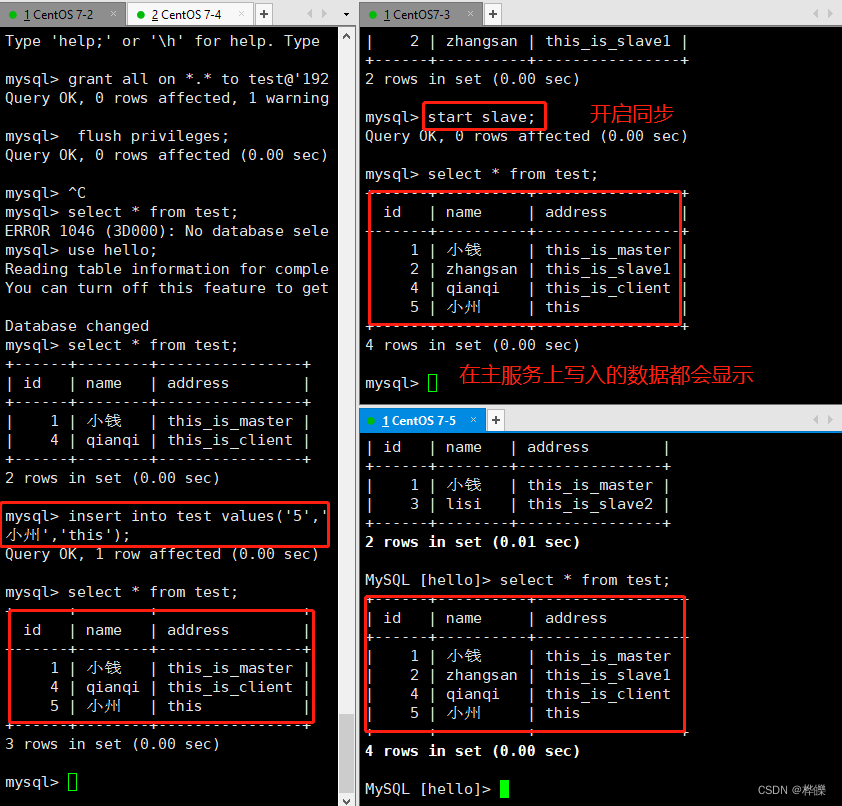
【MySQL 主从复制与读写分离】
目录 一、MySQL主从复制1.1、主从复制架构和原理1.2、MySQL的扩展1.2.1、什么是读写分离1. 读写分离的基本原理2. MySQL 读写分离原理 1.2.2、为什么要读写分离1.2.3、什么时候要读写分离1.2.4、主从复制与读写分离1.2.5、mysql支持的复制类型 1.3、复制的共用1.4、复制架构1.5…
2023年下半年北京/上海/深圳NPDP产品经理认证招生
产品经理国际资格认证NPDP是新产品开发方面的认证,集理论、方法与实践为一体的全方位的知识体系,为公司组织层级进行规划、决策、执行提供良好的方法体系支撑。 【认证机构】
产品开发与管理协会(PDMA)成立于1979年,是…
java学习记录之DBUtils
1 jdbc回顾
1.1 批处理
Statement 执行多条sql addBatch(sql) clearBatch() int[] executeBatch() PreparedStatement 执行一条sql语句,多组参数 addBatch() 执行之前必须设置实际参数 psmt.setXxxx() clearBatch() executeBatch()
1.2 事务
事务&…
SpringBoot 整合redis + Aop防止重复提交 (简易)
1.redis的安装
redis下载 解压 安装
# wget http://download.redis.io/releases/redis-6.0.8.tar.gz
# tar xzf redis-6.0.8.tar.gz
# cd redis-6.0.8
# make
看一下就会有 进入redis-6.0.8下的src目录
[rootVM-16-8-centos redis]# cd redis-6.0.8
[rootVM-16-8-centos re…
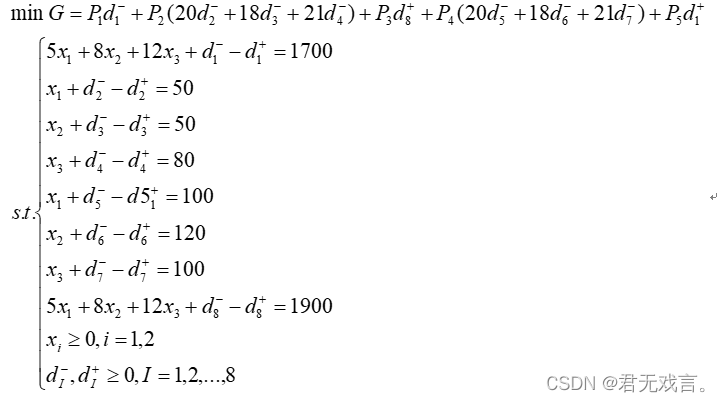





![自动化测试框架[Cypress概述]](https://img-blog.csdnimg.cn/d27b1cca893f45099b1d808b9f9c9d71.png)