leetcode原题链接： 搜索二维矩阵II

题目描述

    编写一个高效的算法来搜索 m x n 矩阵 matrix 中的一个目标值 target 。该矩阵具有以下特性：

• 每行的元素从左到右升序排列。
• 每列的元素从上到下升序排列。

示例 1：

输入：matrix = [[1,4,7,11,15],[2,5,8,12,19],[3,6,9,16,22],[10,13,14,17,24],[18,21,23,26,30]], target = 5
输出：true

示例 2：

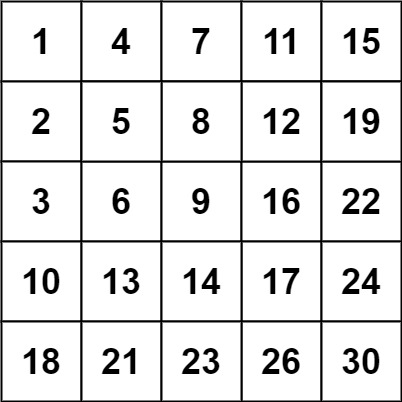
输入：matrix = [[1,4,7,11,15],[2,5,8,12,19],[3,6,9,16,22],[10,13,14,17,24],[18,21,23,26,30]], target = 20
输出：false

提示：

• m == matrix.length
• n == matrix[i].length
• 1 <= n, m <= 300
• -109 <= matrix[i][j] <= 109
• 每行的所有元素从左到右升序排列
• 每列的所有元素从上到下升序排列
• -109 <= target <= 109

解题方法：二分查找。从表格的右上角开始查找，若当前值小于target ,则继续向下查找；若当前值大于target，则继续向左查找，直到查找到解为止。

C++代码

#include <iostream>
#include <vector>
class Solution {
public:
    bool searchMatrix(std::vector<std::vector<int>>& matrix, int target) {
        int n = matrix.size();//行数
        int m = matrix[0].size();//列数
        int i = 0; //第i+1行
        int j = m - 1;//第j+1列
        while (i < n && j >= 0) {
            if (target == matrix[i][j]) {
                return true;
            }
            else if (matrix[i][j] < target) { // 当前值小于target，则扩大搜索范围（向下）
                i++;
            } else { // 当前值大于target，则减少搜索范围
                j--;
            }
        }
        return false;
    }
};