第七章 图

第一节 图的定义

一、逻辑结构
1、逻辑结构
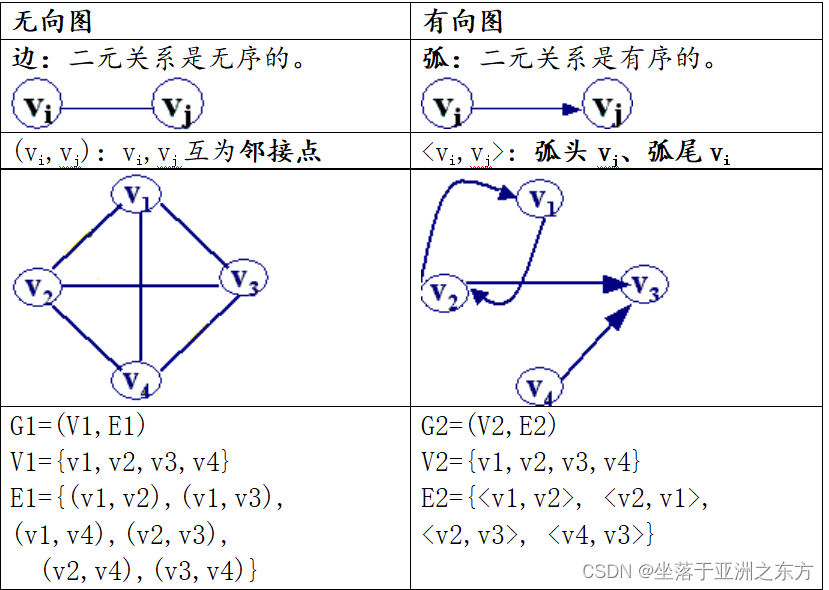
①定义：G=(V,E)。V是顶点集，E是顶点间二元关系的集合。
（内涵越小，外延越大）
②与树的区别：
①树有特殊的根结点；
②树的结点和关系能分成互不相交的若干子集。
③图的分类：

二、基本操作

①对顶点的操作：
InsertVex、DeleteVex、GetVex、SetVex
②对弧/边的操作：
InsertArc、DeleteArc、GetArc、SetArc
③对整体的操作(遍历)：
深度遍历DFSTraverse、广度遍历BFSTraverse

三、常见应用

①信息的组织：
家庭照片管理（与个人照片管理的差别）
②运输问题：
从南京到泰州，最近的路线？换车最少的路线？
电子邮件的路由选择？
③网络的规划：
小区设店的位置选择？
区域规划、城市规划
计算机网络的规划
④进度组织：
工程进度管理
并行计算问题

四、概念术语

思路：考虑图的复杂应用，提供简化问题的思路。

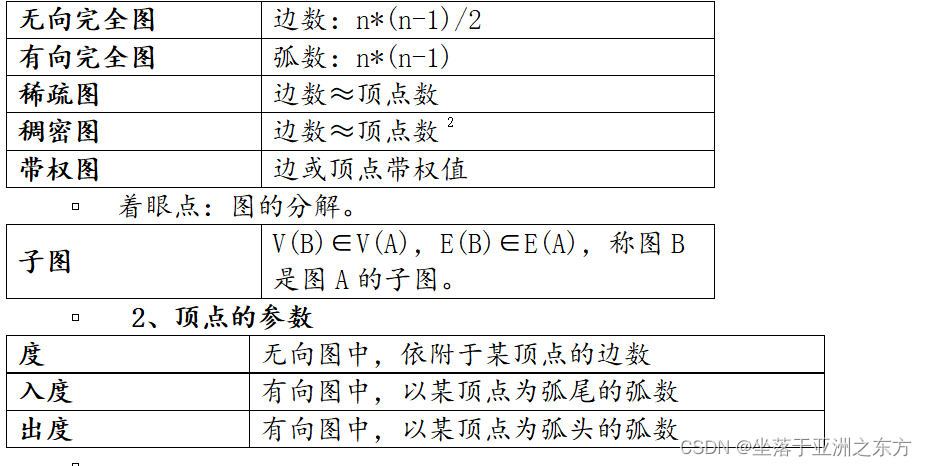
1、图的分类

着眼点：存储结构的选择。

度的应用：以下哪个图能够一笔画完成？为什么？

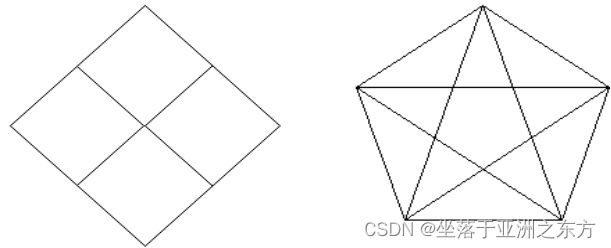
一笔画问题的本质：图结构中的边遍历问题。
应用领域：车间/厂房布置、行走路线的安排…

3、有关路径

着眼点：顶点间的联系。

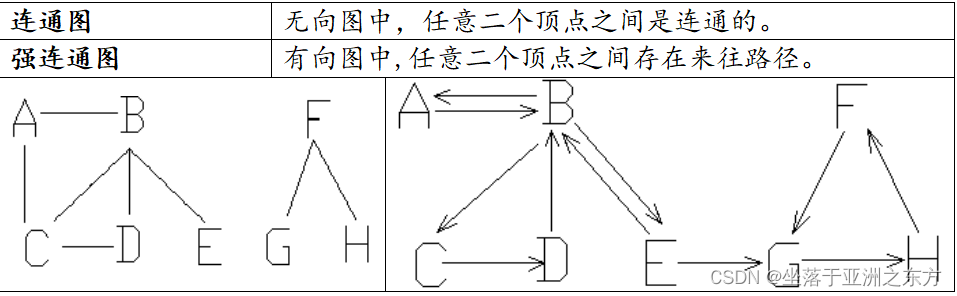
4、有关连通

着眼点：将不连通图简化为连通图。

第二节 图的存储结构

存储结构应该包含：
①顶点的信息；
②边/弧的信息；
③权的信息。

一、数组表示法

1、存储结构

空间复杂度：O(n*n)。

优缺点：
操作方便，适合稠密图。
无向图的arcs[][]为对称矩阵，空间浪费。
当点多边少时，空间浪费多。

2、算法思考

针对以上三图的存储结构，分析：
①在无向图中，如何求顶点i的度？
②在有向图中，如何求顶点i的入度、出度？

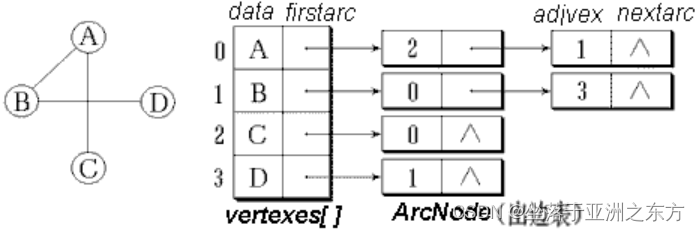
二、邻接表

1、结构分析

图的变化特征：顶点变化少，关系变化多。
顶点表: 顺序结构。边/弧表：动态链表。


带权图的邻接表

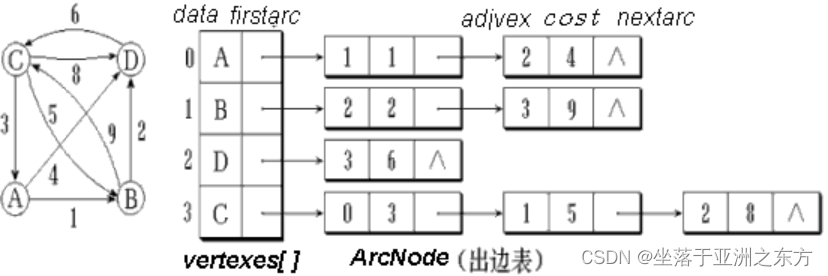
2、建立有向图邻接表的算法

①初始化一个无关系的邻接表结构
void ALGraph_Init(ALGraph &G, VertexType data[],int n)
{ G.vexnum=n; G.arcnum=0; // n为顶点数
G.vertexes=(VexNode )malloc(nsizeof(VexNode));
for(i=0; i<n; i++) // 初始化空关系图
{ G.vertexes[i].data=data[i];
　G.vertexes[i].firstarc=NULL;
}
}
②插入一个弧<v1,v2>
void ALGraph_Insert(ALGraph &G,int v1,int v2)
{ ArcNode *p;
p=(ArcNode *)malloc(sizeof(ArcNode));
p->adjvex=v2;
p->nextarc=G.vertexes[v1].firstarc;
G.vertexes[v1].firstarc=p; //首插入
G.arcnum++;
}
提醒：用不同插入方法，得到邻接表不一样。

3、邻接表的简单应用

①在无向图中，求顶点i的度？
在有向图中，求顶点i的出度？
int ALGraph_OutDegree(ALGraph G, int i)
{ int n; ArcNode *p;
p=G.vertexes[i].firstarc;
for(n=0; p; p=p->nextarc) n++;
return(n);
}
②在有向图中，如何求顶点i的入度？
int ALGraph_InDegree(ALGraph G, int i)
{ ArcNode *p; int k, n=0;
for(k=0; k<G.vexnum; k++)
for(p=G.vertices[k].firstarc; p; p=p->nextarc)
if(p->adjvex==i) n++;
return(n);
}

三、逆邻接表

1、结构分析

弧表中的结点是弧尾。

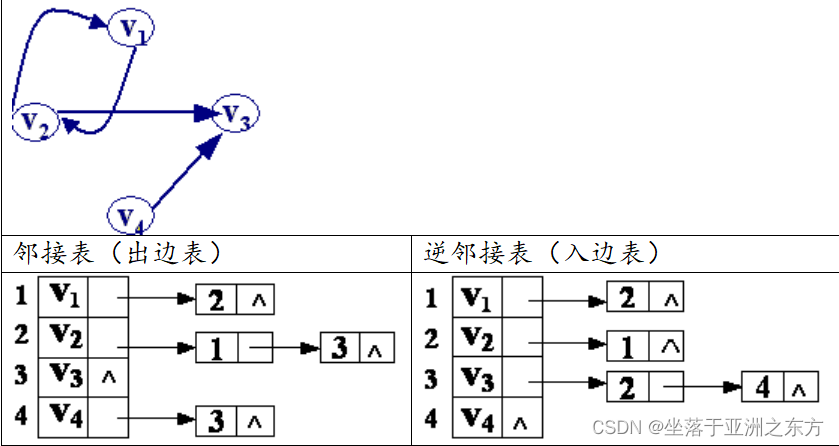
2、算法思考

如何求入度、出度？ 与邻接表恰好相反

第三节 图的遍历

图遍历定义：从某顶点出发，对每个顶点访问且仅访问一次。
图遍历与树遍历的比较：

本节以邻接表为基础讨论算法程序。也可采用其他结构。

一、深度优先搜索DFS(Depth First Search)

1、算法

①设所有顶点都未曾被访问;(设置一个标记数组)
②从起点v出发，访问此顶点，同时设置访问标记；
③依次从v的未被访问过的邻接点出发进行DFS；
(效果：所有与v连通的顶点都被访问过)
④若所有顶点都已访问，则完成；否则，另择起点v，转至②。
例：已知邻接表，求遍历序列。

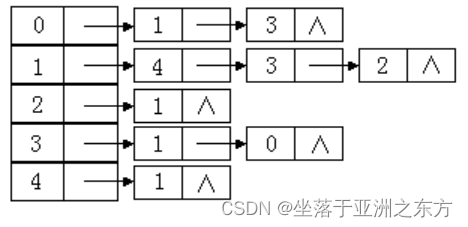
以顶点0为起点的DFS：0，1，4，3，2
以顶点3为起点的DFS：3，1，4，2，0

2、递归程序

类似于树的递归遍历
Boolean visited[MAX]; int time=0; // 用于跟踪程序
// 帽子函数
void DFSTraverse(ALGraph G)
{ if(G.vexnum==0) return;
for(v=0; v<G.vexnum; v++) visited[v]=FALSE; //实现步骤①
for(v=0; v<G.vexnum; v++) //实现步骤④
if(visited[v]==FALSE) DFS(G, v);
}
// 核心函数：遍历顶点v所在的连通分量
void DFS(ALGraph G, int v) //v为起点序号
{ ArcNode *p; int w;
printf(v); visited[v]=TRUE; // 实现步骤②
// 实现步骤③
for(p=G.vertices[v].firstarc; p; p=p->nextarc)
{ w=p->adjvex;
if(visited[w]==FALSE)
DFS(G, w);
}
}
思考：
时间复杂度？ O(e) e为边/弧数

二、广度优先搜索BFS(breadth first search)

相当于树的层次遍历。

1、算法

①设所有顶点都未曾被访问；
②将起点编号加入队列，同时设置访问标记；
③取队首元素，设为v，访问结点v；
④依次将v的各个未被访问过的顶点加入队列，同时设置访问标记；
⑤若队列不空，则循环执行③④，否则⑥；
⑥若所有顶点都已访问，则完成；否则，另择起点V，转至②。
例：已知邻接表，求遍历序列。

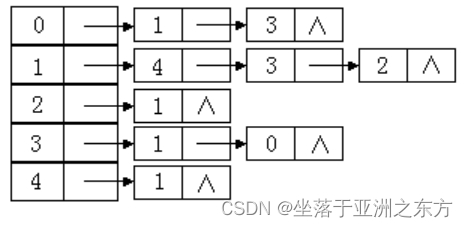
以顶点0为起点的BFS：0，1，3，4，2
以顶点3为起点的BFS：3，1，0，4，2

2、程序

Boolean visited[MAX];
// 帽子函数
void BFSTraverse(ALGraph G)
{ if(G.vexnum==0) return;
for(v=0; v<G.vexnum; v++) visited[v]=FALSE; //实现步骤①
for(v=0; v<G.vexnum; v++) //实现步骤⑥
if(visited[v]==FALSE) BFS(G,v);
}
// 核心函数：遍历顶点v所在的连通分量
// 每个顶点出队列后，被访问
void BFS(ALGraph G,int v)
{ Queue Q; ArcNode *p;
Q_Init(Q);
Q_Enter(Q,v); visited[v]=TRUE; // 步骤②
while(!Q_Empty(Q)) // 步骤⑤
{ v=Q_Leave(Q); printf(v); //步骤③
for(p=G.vertices[v].firstarc; p; p=p->nextarc) //步骤④
{ w=p->adjvex;
if(visited[w]==FALSE)
{ Q_Enter(Q, w); visited[w]=TRUE; }
}
}
}
上机：以邻接表为结构存储图，深度、广度遍历之。

第四节 最小生成树

一、最小生成树(MST:Minimum Spanning Tree)

问题对象：连通无向图G。
MST：各边权值之和最小的生成树。

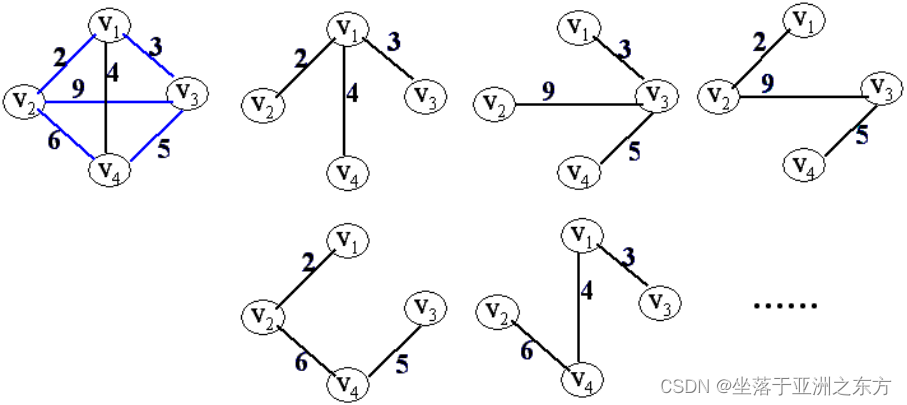
MST的构成：n个顶点，n-1条边。

二、Prim算法

连通图G=(V,E)，从起点v出发，构造最小生成树T=(VT,ET)。

1、算法思路

①初始化VT={v}，ET={ }。
②找权值最小的(Vp,Vq), Vp∈VT, Vq∈V-VT；
③将(Vp,Vq)并入ET，同时Vq并入VT；
④重复②③步骤n-1次。

2、数据结构

①图的结构
需要频繁地读取二点间的权值，采用邻接矩阵。

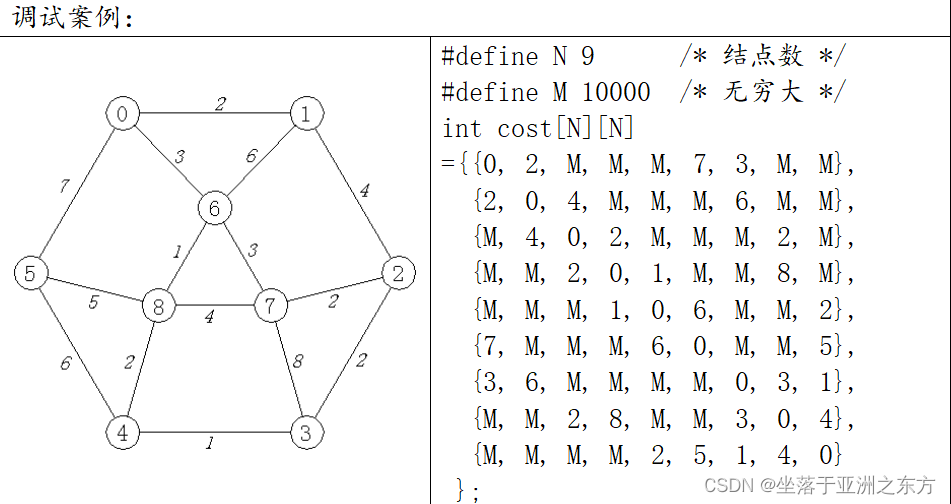
②辅助结构
针对：“找权值最小的(Vp,Vq), Vp∈VT, Vq∈V-VT”
设计结构：VT外每个顶点到VT的最短距离。
typedef struct
{ float distance; // VT外顶点到VT的最短距离
int VexInTree; // VT对应的顶点编号
} ShortDist;
ShortDist SDs[N];
以V4为起点的初始化SDs[N]：

注意：SDs[i].Distance=0的含义：顶点i已在生成树中

3、算法

①初始化SDs[N]；
②在SDs[N]中,找出Distance最小非0值的下标k；
③(SDs[k].VexInTree,k)为生成树的边；
k是VT外某点，SDs[k].VexInTree是VT内某点；
④SDs[k].Distance=0，即顶点k并入生成树；
⑤若cost[k][i]<SDs[i].Distance，修改SDs[i]；
⑥重复②③④⑤

4、程序一：求MST的所有边

为便于程序规范化，补充边/弧结构：
typedef struct { int begin,end,cost;} EDGE;

// v为起点序号, tree[]存储MST的所有边
void MST_prim(int cost[][N],int v,EDGE tree[])
{ ShortDist SDs[N]; int i,j, k,min;
for(i=0;i<N;i++)
{ SDs[i].VexInTree=v; SDs[i].Distance=cost[v][i]; }
for(i=0;i<N-1;i++)
{ for(min=M,j=0; j<N; j++) //找最小非0值的下标k
if(SDs[j].Distance!=0 && SDs[j].Distance<min)
{ min=SDs[j].Distance; k=j; }
tree[i].begin=SDs[k].VexInTree; tree[i].end=k;
tree[i].cost=SDs[k].Distance;
SDs[k].Distance=0; // 将顶点k纳入生成树中
for(j=0; j<N; j++) // 修改SDs[]
if(cost[k][j]<SDs[j].Distance)
{ SDs[j].Distance=cost[k][j]; SDs[j].VexInTree=k; }
}
}
调试案例的执行过程：

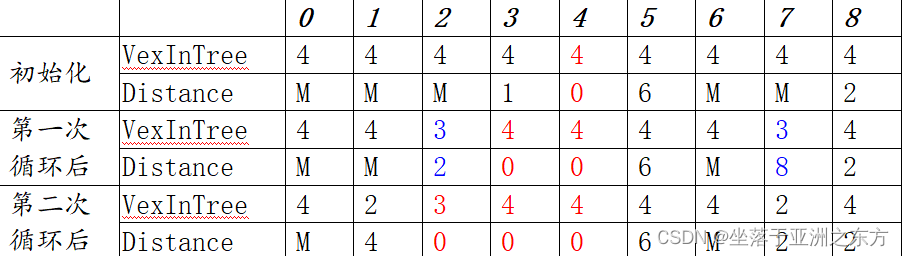
请同学补充完成。

4、算法分析

设图的顶点数为n，
时间复杂度： O(n2)
空间复杂度： O(n)

5、程序二：求MST的树结构

// 生成一棵双亲表示法的树，存于Parent[]中
// v为起点序号
void MST_prim(int cost[][N],int v,int Parent[])
{ ShortDist SDs[N]; int i,j, k,min;
for(i=0;i<N;i++)
{ SDs[i].VexInTree=v; SDs[i].Distance=cost[v][i]; }
Parent[v]=-1;
for(i=0;i<N-1;i++)
{ for(min=M,j=0; j<N; j++) // 找最小非0值的下标k
if(SDs[j].Distance!=0 && SDs[j].Distance<min)
{ min=SDs[j].Distance; k=j; }
Parent[k] = SDs[k].VexInTree;
SDs[k].Distance=0; // 将顶点k纳入生成树中
for(j=0; j<N; j++) // 修改SDs[]
if(cost[k][j]<SDs[j].Distance)
{ SDs[j].Distance=cost[k][j]; SDs[j].VexInTree=k; }
}
}
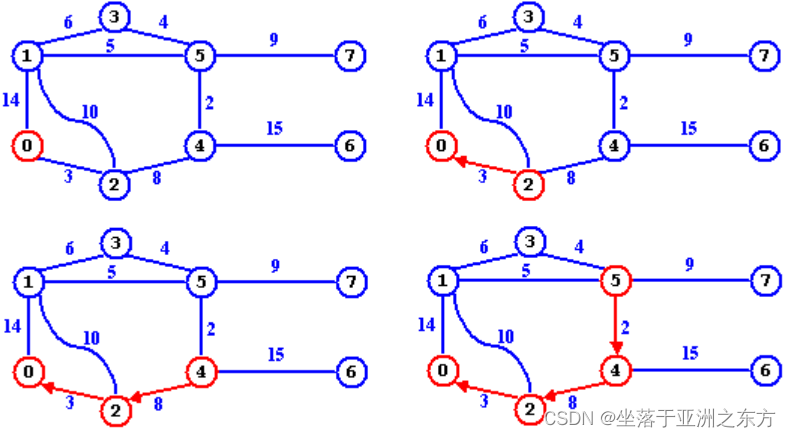
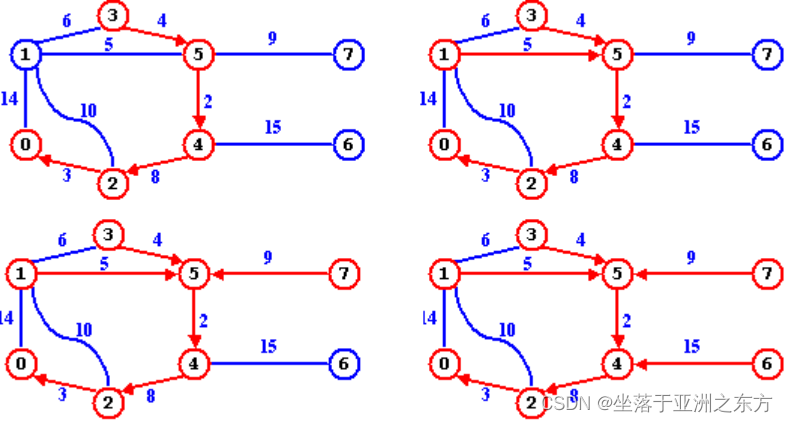
调试案例： 留意Parent[]的变化

三、Kruskal算法

连通图G=(V,E)，构造最小生成树T=(VT,ET)。

1、思路

①尽可能选择n-1条权值最小的边；
②但不能构成回路。

显然，图的存储结构采用有序的边/弧表结构
typedef struct { int begin,end,cost;} EDGE;
typedef struct
{ EDGE *edges; // 边数组
int vn, en; // vn为顶点数, en为边数
} Graph;

2、算法

①初始化VT=V，ET={}，即n个顶点是n个连通分量；
②选择权值最小的边(Vp,Vq)；
③若Vp、Vq不属于同一连通分量，将(Vp,Vq)并入ET；
否则，舍弃。
④重复②③，直至选取了n-1条边。

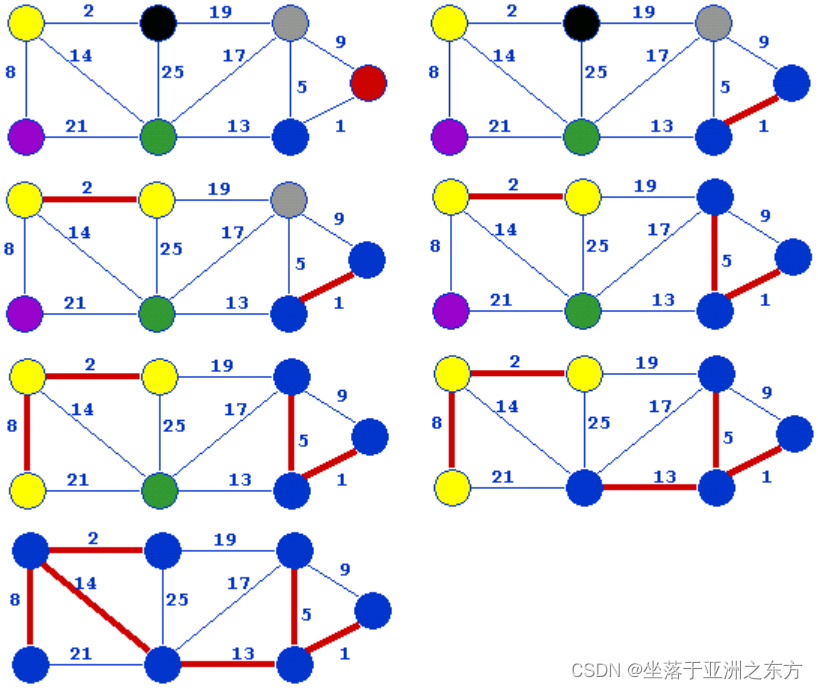
核心操作：连通分量的合并=子集的合并。

3、集合的存储结构

采用树/森林的双亲表示法（子集树）

初始化N个子树： parents[0…N-1]=-1

4、程序：求MST的所有边

// tree[]存储MST的边
void MST_kruskal(Graph G, EDGE tree[])
{ int *parents,begins,ends,i,k;
parents=(int )malloc(G.vnsizeof(int));
for(i=0;i<G.vn;i++) parents[i]=-1;
for(k=0,i=0; i<G.en; i++) // 选边
{ begins=find(parents, G.edges[i].begin);
ends =find(parents, G.edges[i].end);
if(begins!=ends)
{ parents[begins]=ends; // 合并子集树
tree[k] =G.edges[i]; k++;
if(k==G.vn-1) return; // 找到了vn-1条边
}
}
}
求子集编号，即子集树根结点的下标
int find(int parents[],int f)
{ while(parents[f]>=0) f=parents[f];
return(f);
}

5、调试案例

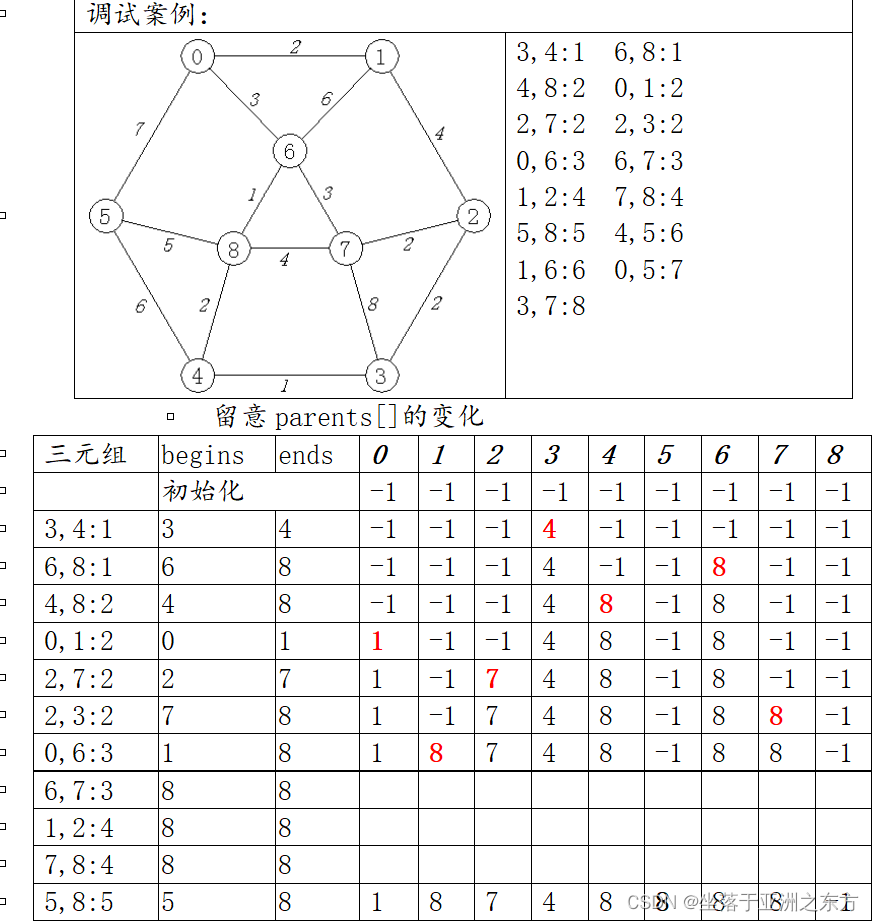
提示：算法完成时，MST的树结构已在parents[]之中。

6、算法分析

设图的顶点个数为n，边数为e。边数组已经按权值有序。
空间复杂度： O(n)
时间复杂度：
“选边” ： 最好O(n)； 最差O(e)
“求子集”： 最好O(log2n)；最差O(n)

7、Prim算法和Kruskal算法的比较

Prim算法： 适合稠密图
Kruskal算法：适合稀疏图

四、程序设计方法之一：贪心法

用局部最优解，组合全局最优解。
作业：
纸笔调试Prim算法、Kruskal算法。
思考题：
如何判断“(e,f)(a,b)(b,c)(g,a)(c,d)(d,e)(f,g)”是否存在环？

第五节 最短路径

路径长度：
无权图：路径上边/弧的个数。
带权图：路径上边/弧的权值之和。
本节对象：带权(权>=0)图
思考：为什么约束：权>=0
提醒：边数多的路径可能比边数少的路径更短。

一、单源点的最短路径(Dijkstra,1959)

1、思路

性质：最短路径由最短子路径组成。
策略：由近及远计算到各顶点的最短路径。

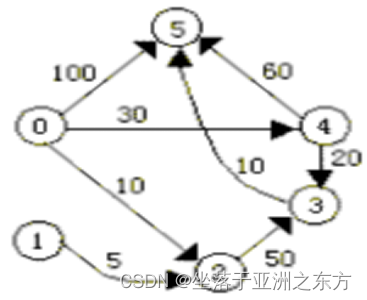
2、数据结构

设G=(V,E)，源点为v。
集合T：已找到最短路径的顶点，初始为{v}。
集合S：其余顶点，S=V-T。
如何表示集合操作？
设立数组set[0,…,N-1]。
初始化set[0,…,N-1]=S, set[v]=T。
如何表示v到各顶点的最短路径长度：
设立数组dist[0,…,N-1]。
初始化 dist[j]=(v,j)的权。
=》图采用邻接矩阵cost[N][N]。

3、算法

①根据源点v，初始化set[]、dist[]；
②从S集中选顶点w，使得dist[w]=Min{ dist[i] }；
③将w并入T；
④修改从v出发到S中各顶点的最短路径长度；
if(dist[w]+cost[w][i]<dist[i]) // 记作三角不等式
dist[i]=dist[w]+cost[w][i]
⑤重复②③④步骤N-1次。
案例演示

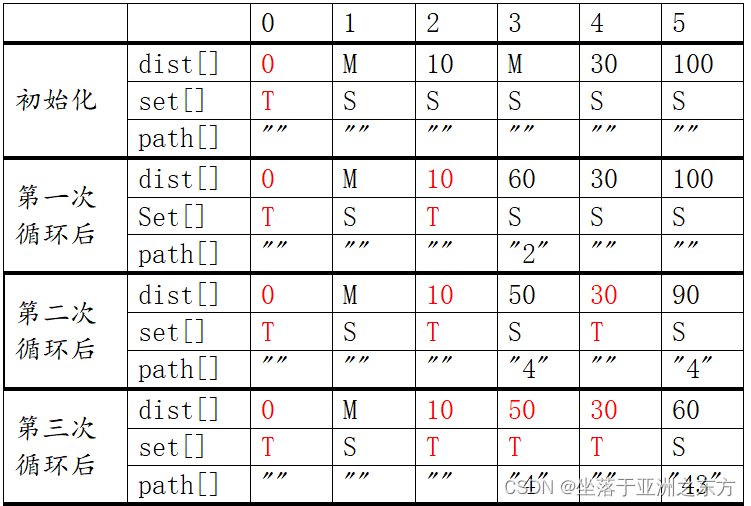
4、程序：求最短路径长度和最短路径。

红色代码仅与最短路径有关。
#define N 6 // 顶点数
#define S 0 // 尚未求出最短路径
#define T 1 // 已经求出最短路径
main()
{ float cost[N][N]={……},
float dist[N]; char path[N][N]; /* 路径字符串 /
dijkstra(cost,0,dist,path); / 起点为顶点0 /
}
//计算v到其余各顶点的最短距离dist[]，最短路径path[N][N]
void dijkstra(float cost[][N],int v,float dist[],char path[][N])
{ int set[N], i,j,nearest_v;
for(i=0; i<N; i++)
{ dist[i]=cost[v][i]; set[i]=S;
path[i][0]=‘\0’; / 路径字符串初始化为空 /
}
for(set[v]=T,i=1; i<N; i++)
{ nearest_v=mincost(dist,set);
for(set[nearest_v]=T,j=0; j<N; j++)
if(set[j]==S && dist[nearest_v]+cost[nearest_v][j]<dist[j])
{ dist[j]=dist[nearest_v]+cost[nearest_v][j];
strcat(path[j],path[nearest_v],nearest_v); //合并路径
}
}
}
//在S集合中找顶点w，dist[w]是dist[]中的最小值/
int mincost(int dist[],int set[])
{ int i,min,w;
for(min=M,i=0; i<N; i++) / N为顶点数 */
if(set[i]==S && dist[i]<min) { min=dist[i]; w=i; }
return(w);
}
// 合并路径
void strcat(char path_j[],char path_w[],int w)
{ int i;
for(i=0; path_w[i]!=‘\0’; i++) path_j[i]=path_w[i];
path_j[i++]=w+‘0’; path_j[i]=‘\0’;
}

5、算法分析

空间复杂度： O(n)
稠密图：采用邻接矩阵结构，时间复杂度为O(n2)
稀疏图：采用邻接表结构，时间复杂度为O(e+nlogn)

6、思考

已知某小区布局图，如何选择最佳设店地址？

二、多源点的最短路径

算法一：重复Dijkstra算法，时间复杂度为O(N3)。
算法二：Floyd算法

1、数据结构

采用邻接矩阵

2、算法

3、程序：求最短路径长度和最短路径。

红色代码仅与最短路径有关。
#define N 5 // 顶点数
main()
{ float cost[N][N]={……};
char path[N][N][N]; /* 路径字符串初始化为空 /
floyd(cost,path)
}
// A[][N]最终变为各顶点间的最短距离，path[N][N][N]为最短路径
void floyd(int A[][N], char path[][N][N])
{ int i,j,k;
for(i=0;i<N;i++)
for(j=0;j<N;j++) path[i][j]=“”; / 初始化为空 */
for(k=0;k<N;k++)
for(i=0;i<N;i++)
for(j=0;j<N;j++)
if(A[i][k]+A[k][j]<A[i][j])
{ A[i][j]=A[i][k]+A[k][j];
strcat(path[i][j],path[i][k],k,path[k][j]);
}
}
//合并路径
void strcat(char p_ij[],char p_ik[],int k,char p_kj[])
{ int i,j;
for(i=0; p_ik[i]!=‘\0’; i++) p_ij[i]=p_ik[i];
for(p_ij[i++]=k+‘0’,j=0; p_kj[j]!=‘\0’; j++,i++)
p_ij[i]=p_kj[j];
p_ij[i]=‘\0’;
}

4、算法分析

时间复杂度：O(N3)。
比邻接矩阵的Dijkstra算法，快常数倍数。
作业：
纸笔调试Dijkstra算法、Floyd算法。

第六节 有向无环图

工程进度安排组织：有向无环图。
活动(Activity)：工程中的子工程。
无环：没有回路。

一、AOV图之拓扑排序

1、概念

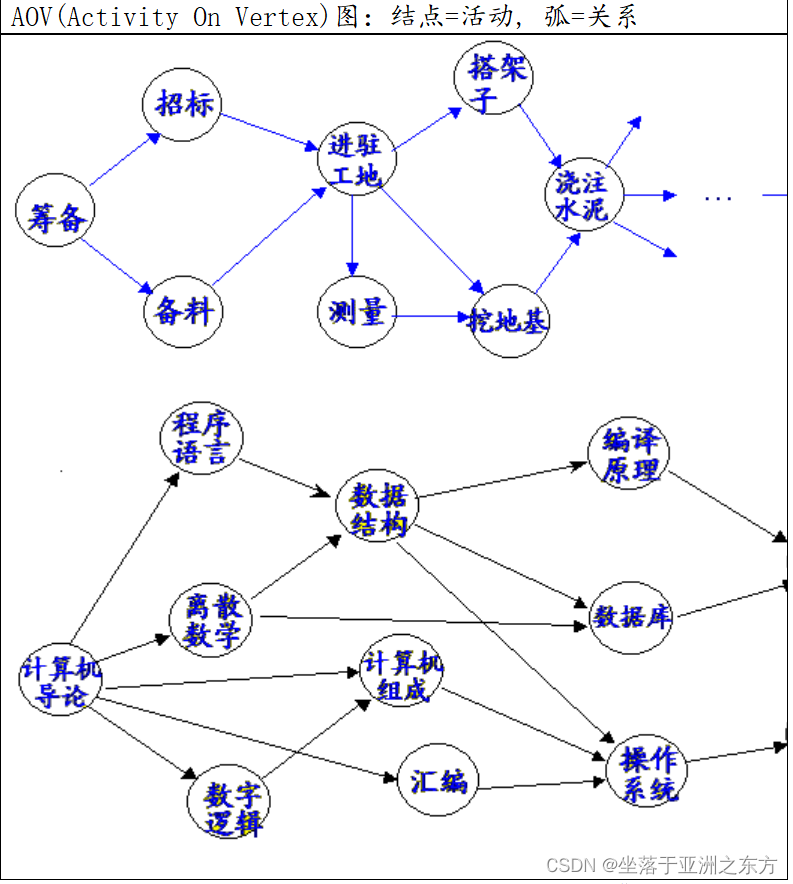
AOV弧集的性质：自反、反对称、可传递。=》偏序关系
全序关系：任意二个结点间存在关系的偏序关系。
拓扑排序：从偏序关系中得到全序序列（拓扑序列）。
提醒：拓扑序列不唯一。

2、算法思路

①选择一个入度为0的顶点v，将其输出；
②删去顶点v及其发出的所有弧；
③重复①②，直至无入度为0的顶点；
④若顶点已全部输出，则网络中无回路；否则，必有回路。
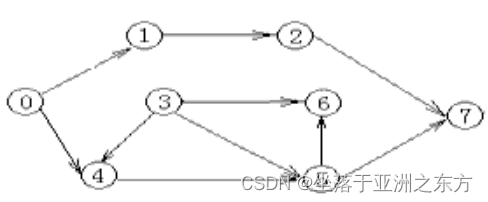
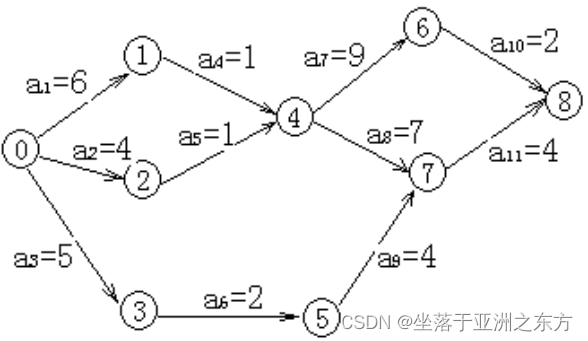
试写出下图的拓扑序列：

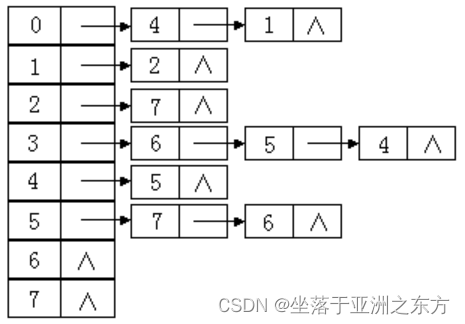
3、数据结构

①设计出发点
需要频繁计算入度=》采用逆邻接表
需要频繁搜索弧头=》采用邻接表
采用十字链表？ 小题大做
②设计方案

4、算法细化

对于入度为0的顶点编号表，采用栈结构加以组织：
①将所有入度为0的顶点编号进栈；
②出栈，输出栈顶元素Vi；
③将Vi的所有后继顶点入度减1；若入度为0，则相应顶点编号进栈；
④重复②③，直至栈空；
⑤若输出顶点数=图中顶点数，则无回路；否则，必有回路。
思考：能否使用队列存储入度为0的顶点编号？

5、程序一：采用顺序栈

struct node //简化：设VexNode和ArcNode相同
{ int vertex;
struct node *link;
};
typedef struct node NODE;

Status toposort(NODE adjlist[],int indegree[],int n,int topo[])
{ int stack,top=0; / 入度为0的顶点编号栈 */
int i,out,k,count=0;
NODE p;
stack=(int )malloc(nsizeof(int));
for(i=0; i<n; i++) / 入度为0者进栈 /
if(indegree[i]==0) { stack[top]=i; top++; }
while(top>0)
{ top–; out=stack[top]; / out为出栈元素 */
topo[count]=out; count++;
for(p=adjlist[out].link; p; p=p->link)
{ k=p->vertex; indegree[k]–;
if(indegree[k]==0) { stack[top]=k; top++; }
}
}
if(count<n) return(FALSE); else return(TRUE);
}
结果topo[]: 3,0,1,2,4,5,6,7

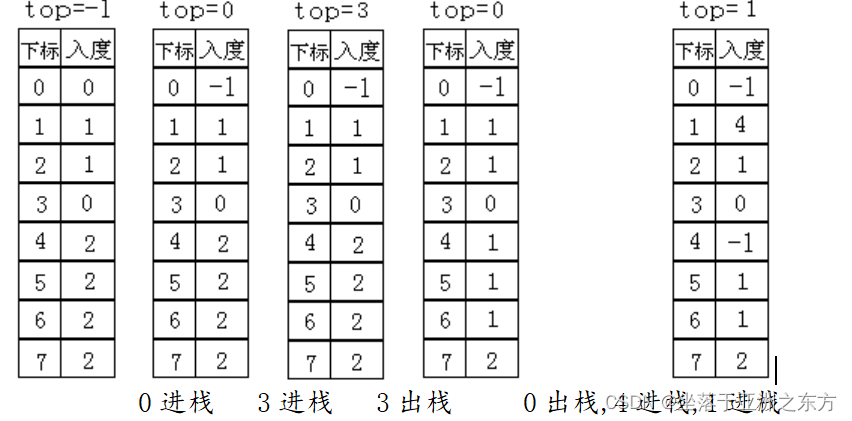
6、程序二：在入度表中实现静态链栈

Status toposort(NODE adjlist[],int indgree[],int n)
{ int i,top=-1,out, k, count=0;
NODE *p;
for(i=0;i<num;i++)
if(indgree[i]==0) { indgree[i]=top; top=i; }
while(top!=-1)
{ out=top; top=indgree[top];
printf("%d, ",out); count++;
for(p=adjlist[out].link; p; p=p->link)
{ k=p->vertex; indgree[k]–;
if(indgree[k]==0) { indgree[k]=top; top=k; }
}
}
if(count<n) return(FALSE); else return(TRUE);
}
入度表的变化过程：

二、AOE图之关键路径(Critical Path)

AOV图的定性分析 => AOE图的定量分析
概要的先后关系 => 精确的时间关系

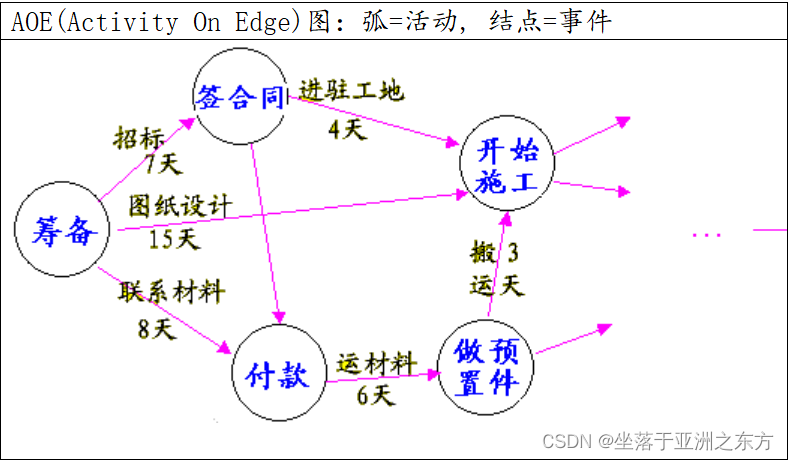
一个源点：入度为0的顶点，对应开工之日。
一个汇点：出度为0的顶点，对应完工之日。

1、AOE图与关键路径

活动的权：活动持续的时间、费用……。
事件：所有入弧活动已完成的状态。
所有出弧活动可以开始的状态。
问题：①完成整个工程所需最短时间？
　②哪些活动是影响进度的关键活动？

完成工程的最短时间：从源点到汇点的最长路径的长度。
关键路径：从源点到汇点的最长路径。

2、算法推导

①分析活动ai
活动ai的最早开始时间early[i]：
从V0=> Vj 的最长路径。
活动ai的最迟开始时间last[i]:
满足不推迟整个工期的要求。
活动ai的时间余量：
last[i]-early[i]
活动ai是关键活动的条件：
last[i]=early[i]
②如何计算early[i]、last[i]？
活动的开始受弧尾事件j、弧头事件k的约束。
先求各事件的最早发生时间v_early[]
最迟发生时间v_last[]
early[i]=v_early[j]
last[i]=v_last[k]- Cjk

③如何计算v_early[]、v_last[]？
前向计算
v_early[源点]=0;
v_early[j]=max{ v_early[i]+ Cij }

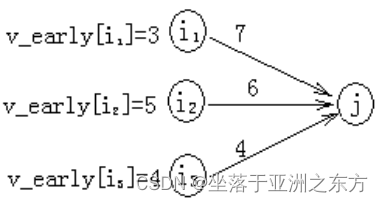
提醒：为保证Vj所有前驱事件的最早发生时间已经求出,必须按拓扑有序序列的次序，依次计算v_early[j]

后向计算
v_last[汇点]=v_early[汇点]
v_last[i]=min{ v_last[j]- Cij }

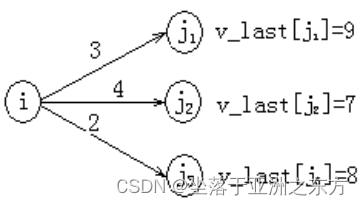
提醒：为保证Vj所有后继事件的最迟发生时间已经求出,必须按逆拓扑有序序列的次序，依次计算v_last[j]。

3、案例演示

4、关键路径算法

1、输入弧数据，建立AOE的存储结构；
2、进行拓扑排序，得到拓扑序列S；
3、从源点出发，按S的次序求最早发生时间v_early[]；
4、从汇点出发，按S的逆序求最迟发生时间v_last[]；
5、计算各弧的early[]、last[]；
6、打印early[i]=last[i]的弧。

第九章 查找

查找表：同类记录的集合。
　　关键字：记录的标识。
　　typedef struct { KeyType key;…… } ElemType;
　　查找：根据给定关键值，在查找表中定位一个关键字等于给定值的记录。
　　查找成功、查找失败
静态查找表：查找表不变
动态查找表：查找表可能变化

第一节 静态查找表

一、顺序表的查找

1、结构

typedef struct
{ ElemType *elem;　//动态、静态顺序表
int length;
}SSTable;

2、无序顺序表的顺序查找算法

从表的一端开始，逐个比较记录的关键字。
int search_seq(SSTable ST, KeyType key1)
{ for(i=0; i<ST.length; i++)
if(ST.elem[i].key==key1) return(i);
return(-1); //查找失败的标记
}

3、有序顺序表的顺序查找算法

int search_seq(SSTable ST, KeyType key1) // 增序顺序表
{ for(i=0; i<ST.length && ST.elem[i].key<=key1; i++)
if(ST.elem[i].key==key1) return(i);
return(-1); //查找失败的标记
}

4、性能分析

针对无序顺序表的顺序查找算法
时间复杂度：O(n) ＝》效率低
　平均查找长度：比较次数的期望值。
　
Pi ：查找第i条记录的概率
Ci ：找到第i条记录的比较次数。
例：等概率查找成功的情形：

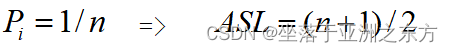
5、算法补充

查找最大值、最小值；
查找最小值的下标；
查找次小值的下标；

二、有序顺序表之折半查找算法

1、算法思路

查字典的方法：逐步缩小查找范围，直至得到结果。

2、算法

最小关键值记录的位置：low
最大关键值记录的位置：high
中间位置：mid=(low+high)/2
// ST.elem[0]…ST.elem[ST.length-1]是线性增序表
int bin_search(SSTable ST, KeyType key1)
{ int low,high,mid;
low=0; high=ST.length-1;
while(low <= high) // 留意=号
{ mid=(low+high)/2;
if(key1==ST.elem[mid].key) return(mid);
if(key1< ST.elem[mid].key) high=mid-1;
else low=mid+1;
}
return(-1);
}

2、性能分析

设顺序表各元素编号：0,1,2,3,4,5,6,7
二叉判定树：

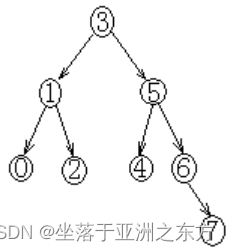
除最低层外是一棵满二叉树。
树的深度为
查找成功的比较次数＝该记录的深度。
查找失败的比较次数＝树的深度。
例：等概率查找成功的情形：

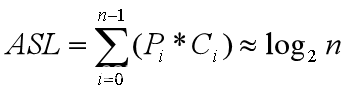
(理由：半数以上的结点处于最低二层中)

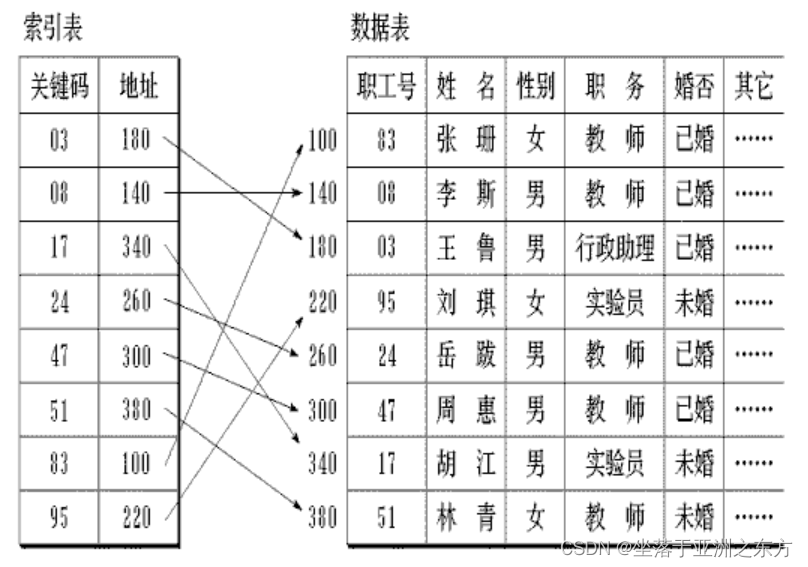
四、索引顺序表的查找

1、稠密索引策略

一个索引项对应一条记录。适用于：记录无序存放的结构。

2、稀疏索引策略

一个索引项对应一组记录(子表)。
适用于：子表间记录必须有序，子表内记录必须无序。

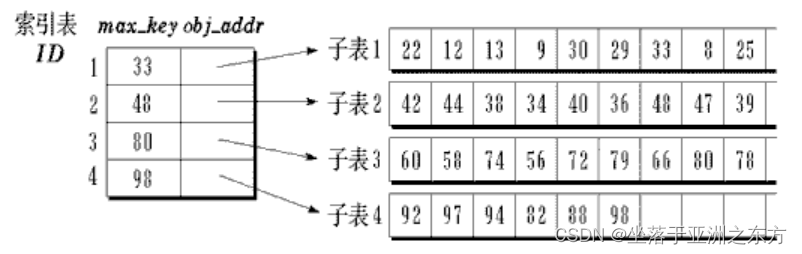
性能分析
　　 ASL=索引表的ASL＋子表内ASL

例：查找表长为n，块长为s，索引项数b=n/s，对索引表进行折半查找，对子表进行顺序查找。请计算ASL。
　　ASL=log2b+s/2

3、多级索引策略

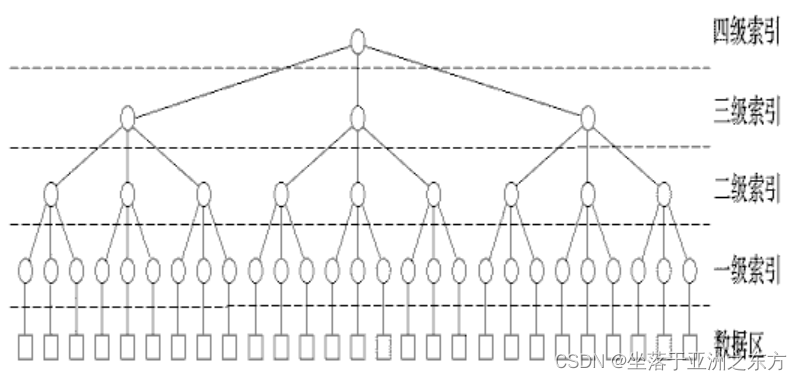
4、倒排表(Inverted Index List)策略

适用于：针对大数据表的多方式查找。

主关键码：唯一地标识该对象。
主索引表：用主关键码建立的索引表。
主索引表的结构：(关键码、记录存储地址)。
次关键码：其他一些经常搜索的属性。
次索引表：对每一个次关键码建立的索引表。
次索引表的索引项结构：
［次关键码的索引值、指针］
指针指向在该属性上具有该索引值的所有记录
倒排表：符合上述结构的次索引表。

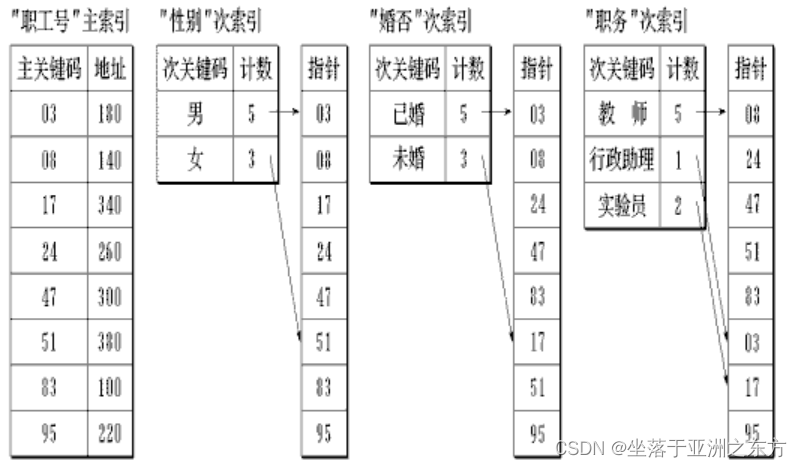
“倒排”的来由：在一般文件组织中的查找，是先找到记录，再找到该记录的属性值。而在上述查找，是先给定某属性值，再查找含有该属性值的记录。
作业：

1、已知某有序顺序表，计算其折半查找的ASL。

2、已知某索引顺序表的结构，计算其ASL。

第二节 动态查找表
表结构在查找过程中动态生成。
动态：查找失败，将新记录插入查找表。

一、二叉排序树

1、定义

在二叉排序树中，对于每个结点p：
若左子树非空，其中所有结点的关键值小于p的关键值；
若右子树非空，其中所有结点的关键值大于*p的关键值。

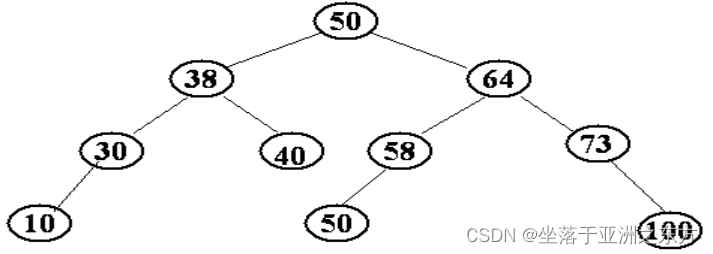
struct BSTNode
{ ElemType elem;　
struct BSTNode *lchild,*rchild;
};
typedef struct BSTNode BSTNode;
用途：
排序(中序遍历)。
查找(二叉查找树)

2、查找算法

在二叉排序树*root中，找键值为x的结点地址。
BSTNode *search(KeyType x, BSTNode *root)
{ while(root)
{ if(x==root->elem.key) return(root);
if(xelem.key) root=root->lchild;
else root=root->rchild;
}
return(NULL);
}
性能分析：
ASL：最好情况为O(log2n)，相当于折半查找。
最差情况为O(n)， 相当于顺序查找。

3、插入算法

若二叉排序树为空时？
若二叉排序树不为空？
示例：Keys={50,35,70,40,51,65,20,80}

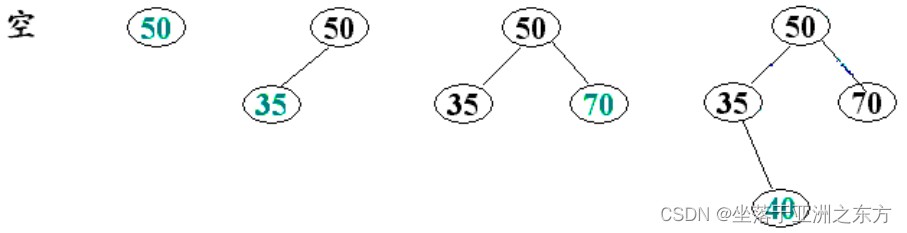
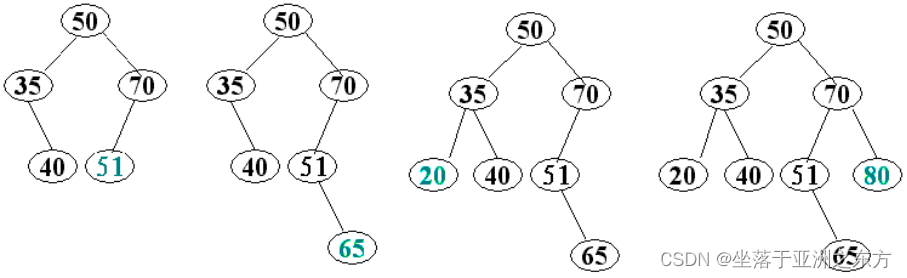
在根指针为root的二叉排序树中插入结点*newp
BSTNode * insert(BSTNode *root, BSTNode *newp)
{ BSTNode *p=root;
if(root==NULL) return(newp);
while(1)
{ if(newp->elem.key < p->elem.key)
if(p->lchild) p=p->lchild;
else { p->lchild=newp; return(root); }
else
if(p->rchild) p=p->rchild;
else { p->rchild=newp; return(root); }
}
}

4、应用实例：统计文件中字母、单词的使用次数

结构：
struct node
{ char word[M]; //单词
int weight; //出现次数
struct node *lchild, *rchild;
}
算法：
①每读入一个单词，查找二叉排序树
②查找成功，weight++；查找失败，插入新结点。
③中序输出二叉排序树。
上机：
已知某关键值序列，构造二叉排序树，中序遍历之。
第二节 动态查找表

二、二叉平衡树(AVL树)

问题由来：二叉排序树可能出现退化。
目标 ：二叉排序树是AVL树。

1、定义

二叉平衡树是：
一个空树；或：
1)左右子树均为二叉平衡树；
2)左右子树的深度之差的绝对值<=1。
结点*p的平衡因子： 左子树深度-右子树深度。
depth(p->lchild) - depth(p->rchild)
二叉平衡树：所有结点的平衡因子=0或-1或1
编程：设二叉树结点结构含4个域：lchild、data、bf、rchlid，设计算法，求树中所有结点的平衡因子bf。
struct BSTNode
{ ElemType elem;
int bf; 　
struct BSTNode *lchild,*rchild;
};
typedef struct BSTNode BSTNode;

void bf(BSTNode *root)
{ if(!root) return;
root->bf=depth(root->lchild)-depth(root->rchild);
bf(root->lchild);
bf(root->rchild);
}
int depth(BiTNODE *root)
{ int left,right;
if(root==NULL) return(0);
left =Depth(root->lchild);
right=Depth(root->rchild));
return(max(left,right)+1);
}

第三节 哈希(hash)表

查找算法的基础：比较、计算。

一、定义

1、哈希方法的由来

能否通过对关键值的计算，直接得到待查记录的地址？
显然，记录的存放规则和查找规则必须一致。
规则=》哈希表函数(映射：关键值=>记录位置)
哈希函数值称为哈希地址。
哈希表: 按哈希表函数值来组织的查找表。

以计算为基础的查找方法，妙！

2、哈希查找的问题

能不能保证映射关系的一一对应？
关键值的分布：广、散 (如：0,5,15…)，
查找表的地址空间：小、密集(如：0,1,2…)，
可能存在关键值相同的记录。
不同关键值的记录，有相同的哈希地址：冲突。
冲突的关键值：同义词。
目标：均匀的哈希函数
哈希地址均匀分布在整个地址空间，冲突次数少。

二、哈希函数的构造

哈希函数的好坏，必须结合查找表的情况来分析。

1、直接定址法

直接取关键字的某个线性函数值作为哈希地址
如： hash(key)=key-1949

2、数字分析法

当关键字值的数位较多时，取其中几位作哈希地址。
如：以学号为关键字的情形: 867201……867266

3、取模法

将关键字值除以一个整数后所得的余数作为哈希地址。
可以保证哈希地址在有效的地址空间之内。

4、平方取中法

计算关键字值的平方，取中间若干位作为哈希地址。

5、叠加法

思路与平方取中法同出一辙，提高了计算速度。
将关键字值分成几部分，之和作为哈希地址。
好的哈希函数：
①计算效率高
②函数值不越界
③函数值的分布均匀
实际的哈希表，会多开辟一些的空间，以减少冲突。
装填因子＝表中记录数/表长度
装填因子值大 =》 冲突可能性大。

三、哈希函数实例：高级语言中的关键字搜索系统

在编译过程中，需要频繁搜索关键字。
关键字表被设计成一个哈希表，可以找到一个不发生冲突的优秀哈希函数。
例：在Pascal语言中, 有26个关键字(保留字)。
哈希函数：H(Key)=L+g(key[1])+g(key[L])
L：关键字长度
key[1]：关键字的第一个字符
key[L]：关键字的最后一个字符
g(x)： 从字符到数字的转换函数
四、冲突处理方法
冲突不可避免！

1、开放地址法

出现冲突时，沿一个地址序列逐个探测，直到找出一个空闲空间，将冲突记录存于此间。
只要哈希表不满，总是可行的。
Hi=(H(key)+di) MOD m
H(key)：哈希函数，
m： 哈希表长，
di： 增量序列。
根据di的取法，又分为：

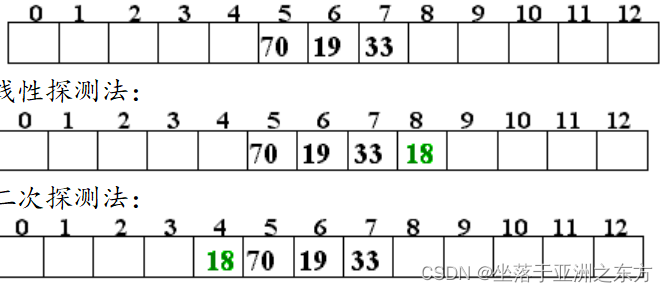
1)线性探测法 di=1,2,…m-1

2)二次探测法 di=1,-1,22,-22,…,k2,-k2

设某哈希表结构如下，H(k)=k MOD 13。现插入第4个记录(关键值为18)。

3)伪随机探测法

H0=H(key)
Hi=(Hi-1+p) MOD m p为质数

4)再哈希法

计算另一哈希函数，得到另一地址。以求避免冲突。
开放地址法小结：
优点：充分地利用了哈希表的空间
缺点：解决一个冲突，就为下一个冲突埋下了伏笔。

2、链地址法

方法一：将哈希表分成基本区和溢出区。

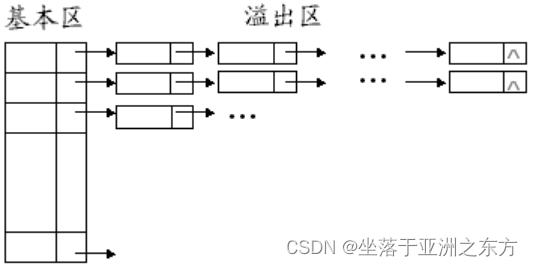
方法二：定义一个指针数组，指向哈希地址相同的记录链。

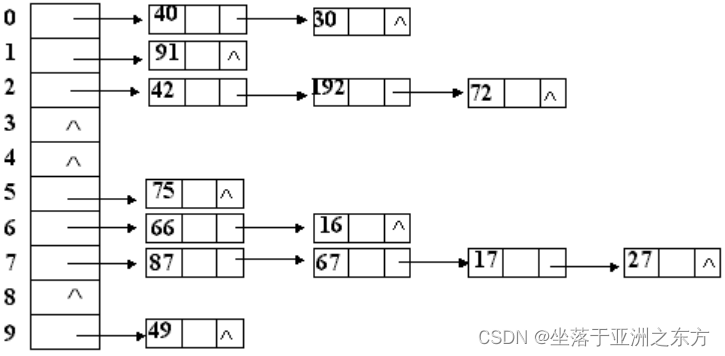
例：设哈希表为[0:9]，哈希函数为H(k)=k Mod 10。将关键值为75,66,42,192,91,40,49,87,67,16,17,30,72,27的记录依次插入哈希表，请写出哈希表结构。

优点：查找性能高。
缺点：空间利用率降低。

五、性能分析

在开放地址法中：
反复计算比较，直至成功或遇到空闲单元(失败);
在链址法中：
一次计算，反复比较，直至成功或无结点可比较(失败)。

哈希查找的关键：
①根据数据的情形设计均匀的哈希函数
②合适的冲突处理方法。
例1：Hash表的地址空间为0…5，散列函数为H(key)=key mod 6，采用线性探测法处理冲突，将10，5，9，3，11依次存入Hash表，那么查找元素3，需要比较 次。
A、1 B、2 C、3 D、4
例2：针对上表计算，在等概率查找的情形下，查找成功时的平均查找长度？查找失败时的平均查找长度？

第十章 内部排序

排序：调整记录表中记录次序，使之按关键值有序(增序)。
记录表结构

内部排序：记录集全部在内存中。
类似战术问题。
外部排序：记录集部分在内存中，排序过程中，需访问外存。
类似战略问题。

稳定性：关键值相同的记录，排序前后的相对次序不变。
例：5 1 4 3 4 => 1 3 4 4 5 稳定
=> 1 3 4 4 5 不稳定

第一节 插入排序

一、直接插入

1)思路

起源于数据陆续达到的思路，摸牌的行为。

2)算法

设已存在一个有序子序列；
每趟：将一个记录按关键值大小插入到有序子序列中。
初始化时，有序子序列只有一个记录；
n-1趟后，有序子序列有n个记录。

3)程序

void InsertSort(SqList &L) // 增序
{ int i,j; RecordType tmp;
for(i=1; i<L.length; i++)
{ tmp=L.r[i];
for(j=i-1; j>=0 && L.r[j].key>tmp.key; j–)
L.r[j+1]=L.r[j]; //移位
L.r[j+1]=tmp;
}
}

时间复杂度？ O(n2)
稳定排序？ 稳定

第二节 交换排序

基本思想
记录间两两比较关键字，若为逆序，则交换位置。

一、简单交换排序

1、思路

相邻记录间两两比较、交换。

2、二种方案

冒泡排序
从后向前比较，小值向前移位

3、冒泡程序

void BubbleSort(SqList &L)
{ int i,j,flag; RecordType tmp;
for(i=0; i<L.length-1; i++)
{ flag=0; //避免无交换的排序趟
for(j=L.length-1; j>i; j–)
if(L.r[j].key<L.r[j-1].key)
{ tmp=L.r[j]; L.r[j]=L.r[j-1]; L.r[j-1]=tmp;
flag=1;
}
if(flag==0) break;
}
}
时间复杂度？ O(n2)
稳定排序？ 稳定排序

二、快速排序

1、由来

冒泡、沉底法：每趟将极大/小数置入到目标位置。
为什么不将中位数置入目标位置上呢？
如何确定中位数？
折中=》如何将任意值置入目标位置？

2、分治法的框架

设有序列a[L]……a[H]，将任选记录置入目标位置a[i]，
原序列分解二个子序列：
a[L]……a[i-1]：关键值均小于a[i]；
a[i+1]……a[H]：关键值均大于a[i]。
对二个子序列，快速排序。
void QuickSort(SqList &L,int low,int high)
{ if(low>=high) return; //子序列只有一个记录
i=Partition(L, low, high);
QuickSort(L,low,i-1);
QuickSort(L,i+1,high);
}

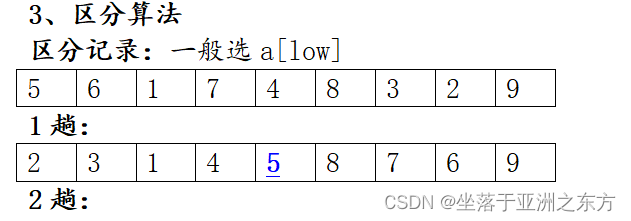
3、区分算法

区分记录：一般选a[low]

4、区分程序

int Partition(SqList &L,int low,int high)
{ int i,j; RecordType tmp;
i=low; j=high; tmp=L.r[low];
while(i<j)
{ while(i<j && L.r[j].key>=tmp.key) j–;
if(i<j) { L.r[i]=L.r[j]; i++; }
while(i<j && L.r[i].key< tmp.key) i++;
if(i<j) { L.r[j]=L.r[i]; j–; }
}
L.r[i]=tmp;
return(i);
}

5、分析

时间复杂度？ 一般情况为O(nlog2n)，拆分过程近似平衡树
最糟情况为O(n2)，类似冒泡、沉底
空间复杂度？
栈空间=树的深度。
最好情况：树深度=log2n
最糟情况：树深度=n
稳定排序？不稳定
什么是最糟情况？
已经有序的数组。
例、一组记录的关键值为(4,7,5,2,3,8)，进行从小到大的快速排序，以首记录为基准，得到的第一趟排序结果为 。
A、2,3,4,5,7,8 B、3,7,5,2,4,8
C、3,4,5,2,7,8 D、3,2,4,5,7,8
作业：
纸笔调试快速排序。
第三节 选择排序
由来：
“比较”比“赋值”速度快得多

一、直接选择排序

算法：
n-1趟选出n-1个极值，置于相应目标位置。
void SelectSort(SqList &L)
{ int i,j,min_i; RecordType tmp;
for(i=0; i<L.length-1; i++)
{ min_i=i;
for(j=i+1; j<L.length; j++)
if(L.r[j].key<L.r[min_i].key) min_i=j;
if(i!=min_i)
{ tmp=L.r[i]; L.r[i]=L.r[min_i]; L.r[min_i]=tmp; }
}
}
时间复杂度？ O(n2)
稳定排序？ 不稳定！
例： 3 4 5 3 1 2
1 4 5 3 3 2

二、堆排序

1、由来

1)能不能减少比较次数呢？

2)KMP算法的启发：充分利用前面比较的结果。

3)锦标赛的赛制： 树形选择

选出冠军的过程：


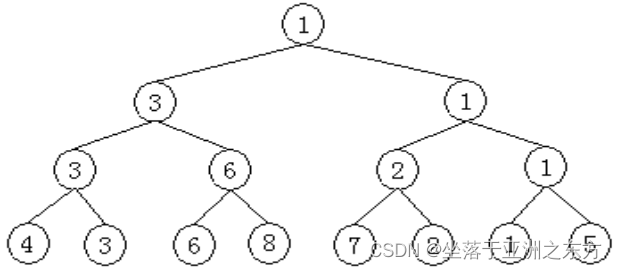
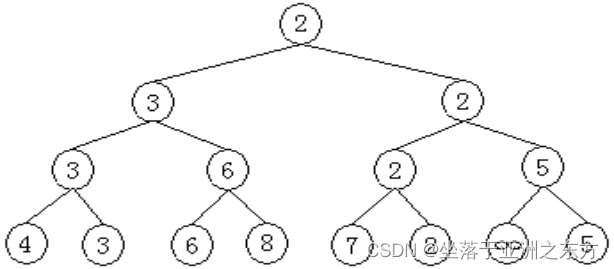
选出亚军的比较次数=树的深度log2n
时间复杂度？ O(nlog2n)
空间复杂度？ O(n)

2、堆的定义

60 年代Williams首先提出堆排序算法。 
有n个记录的序列,其关键值序列为(K0,K1,……Kn-1) 

若2i+1<n，则有Ki<=K2i+1
若2i+2<n，则有Ki<=K2i+2
实际上，该序列可视作一棵完全二叉树的顺序存储形式。
堆中：每个分支结点的关键值 <= 其左右孩子结点的关键值

3、堆排序算法

如何建堆？找到最小值？
建堆是一个调整的过程。
从头开始调整？或从尾开始调整？
从简单的事做起！
从最后一个分支结点开始调整！

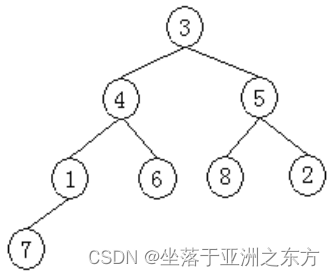
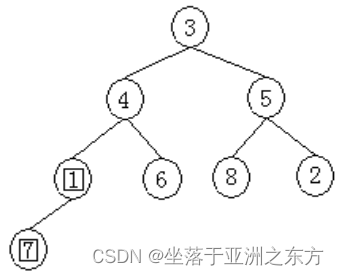
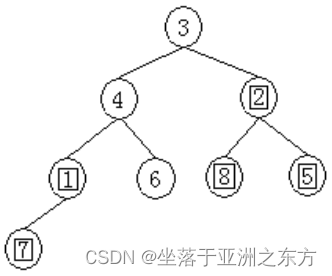
4、示例

原序列：3,4,5,1,6,8,2,7
①建堆过程：

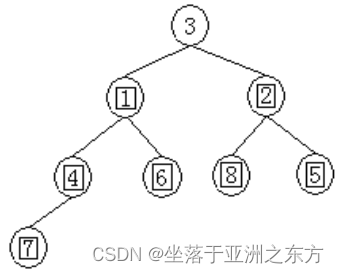
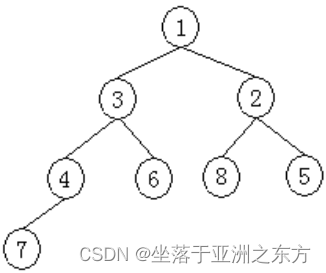
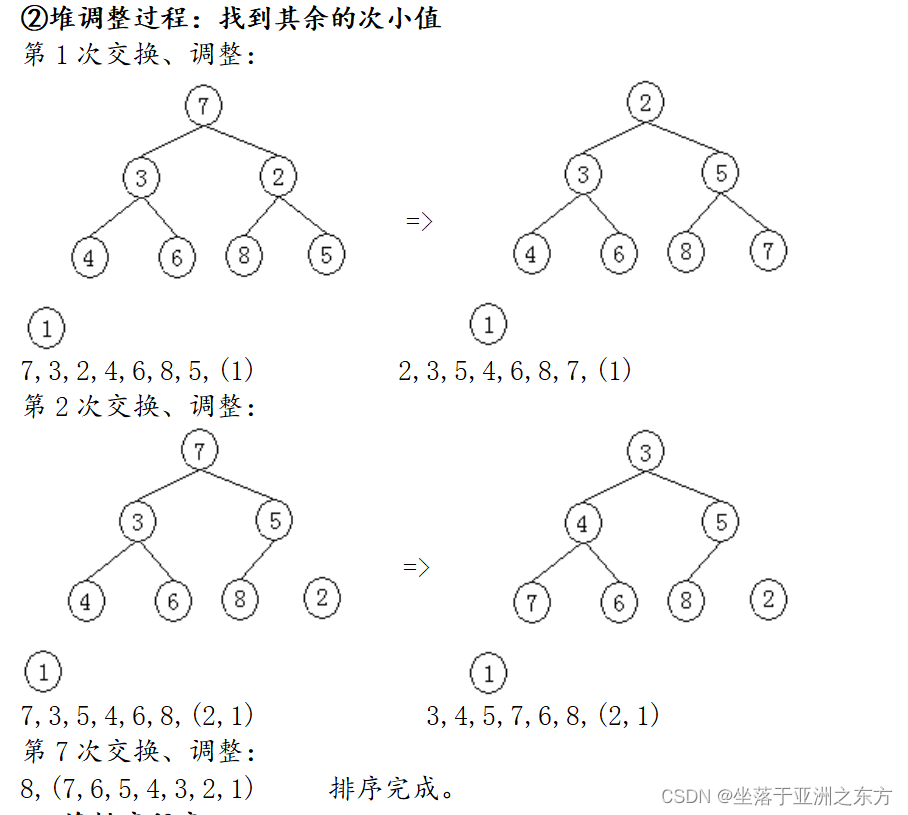
4、堆排序程序

void HeapSort(SqList &L)
{ int i; RecordType tmp;
for(i=L.length/2-1; i>=0; i–)
HeapShift(L,i,L.length-1);
for(i=L.length-1; i>0; i–)
{ tmp=L.r[0]; L.r[0]=L.r[i]; L.r[i]=tmp;
HeapShift(L,0,i-1);
}
}
// 调整范围：L.r[root]……L.r[bottom]
void HeapShift(SqList &L,int root,int bottom)
{ RecordType tmp; int ch_i;
tmp=L.r[root];
ch_i=2root+1;
while(ch_i<=bottom)
{ if(ch_i+1<=bottom && L.r[ch_i].key>L.r[ch_i+1].key)
ch_i++; // ch_i是左右孩子中较小者的下标
if(L.r[ch_i].key>=tmp.key) break;
L.r[root]=L.r[ch_i];
root=ch_i; ch_i=2root+1;
}
L.r[root]=tmp;
}
时间复杂度？
整个算法O(nlog2n)，建堆O(n)
空间复杂度？ O(1)
稳定排序？ 不稳定

原来2个3，谁先谁后？
直观的理由：比赛分组不同，结果有差异。
例：一组记录的关键值为(4,7,5,2,3,8)，利用堆排序算法建立的初始堆为 C 。
A、2,4,5,7,3,8 B、4,2,5,7,3,8
C、2,3,5,7,4,8 D、8,3,5,7,4,2
作业：
纸笔调试堆排序。

第四节 归并排序

由来：

1)二个有序序列归并为一个有序序列的速度快。
2)大集合的排序：先对子集排序，再归并。
3)外排序的需要
2路归并、3路归并、多路归并。
一、基本操作：归并二个相邻的有序子表
2路归并：归并二个前后相邻的有序子表。
//将SL.r[L1]…SL.r[H1]与SL.r[H1+1]…SL.r[H2]归并到TL.r[L1]…TL.r[H2]
void Merge(SqList SL,SqList &TL,int L1,int H1,int H2)
{ int i,j,k;
i=L1; j=H1+1; k=L1;
while(i<=H1 && j<=H2)
if(SL.r[i].key<=SL.r[j].key) TL.r[k++]=SL.r[i++];
else TL.r[k++]=SL.r[j++];
while(i<=H1) TL.r[k++]=SL.r[i++];
while(j<=H2) TL.r[k++]=SL.r[j++];
}

二、归并排序的过程

1、初始化时：有序子表长度为1。
2、相邻子表两两归并，有序子表加倍；
3、循环执行2，直至有序子表长度为N。
举例：
原 表：3,2, 5,1, 6,8, 4 子表长度=1
第1趟：2,3, 1,5, 6,8, 4 子表长度=2
第2趟：1,2,3,5, 4,6,8 子表长度=4
第3趟：1,2,3,4,5,6,8 子表长度=7

总趟数？

三、自下向上的思路

一、2路归并排序中的一趟

void Mergepass(SqList SL,SqList &TL,int len)
{ int i;
for(i=0; i<=SL.length-2len; i=i+2len)
Merge(SL,TL,i,i+len-1,i+2*len-1);
if(i+len+1 <= SL.length)
Merge(SL,TL,i,i+len-1,SL.length-1);
else
while(i<SL.length) TL.r[i++]=SL.r[i];
}

二、归并排序主函数

void MergeSort(SqList &L)
{ SqList Temp;
int i,len=1;
while(len<SL.length)
{ Mergepass(L,Temp,len); len=len2;
if(len<SL.length)
{ Mergepass(Temp,L,len); len=len2; }
else
for(i=0;i<L.length;i++) L.r[i]=Temp.r[i];
}
}
时间复杂度？ O(nlog2n)
空间复杂度？ O(n)
稳定排序？ 稳定
作业：
纸笔调试归并排序。
例、下列排序算法中， 是稳定的。
A、冒泡排序 B、快速排序 C、选择排序
D、堆排序 E、插入排序
练习：现有一个顺序表含有10000个记录，其中只有少量记录次序不对，且它们距离正确位置不远；如果以比较和移动次数作为度量，请问采用哪种排序方法较好？为什么？
快速 X
堆 X 跳远了
归并 ：空间大， 全部logn趟完成，才算完成
插入： 每趟必须做，只是每趟的工作量小些
在程序中，可能需要为某些整数定义一个别名，我们可以利用预处理指令#define来完成这项工作，您的代码可能是：

#define MON 1
#define TUE 2
#define WED 3
#define THU 4
#define FRI 5
#define SAT 6
#define SUN 7
在此，我们定义一种新的数据类型，希望它能完成同样的工作。这种新的数据类型叫枚举型。

1. 定义一种新的数据类型 - 枚举型

以下代码定义了这种新的数据类型 - 枚举型

enum DAY
{
MON=1, TUE, WED, THU, FRI, SAT, SUN
};
(1) 枚举型是一个集合，集合中的元素(枚举成员)是一些命名的整型常量，元素之间用逗号,隔开。

(2) DAY是一个标识符，可以看成这个集合的名字，是一个可选项，即是可有可无的项。

(3) 第一个枚举成员的默认值为整型的0，后续枚举成员的值在前一个成员上加1。

(4) 可以人为设定枚举成员的值，从而自定义某个范围内的整数。

(5) 枚举型是预处理指令#define的替代。

(6) 类型定义以分号;结束。

2. 使用枚举类型对变量进行声明

新的数据类型定义完成后，它就可以使用了。我们已经见过最基本的数据类型，如：整型int, 单精度浮点型float, 双精度浮点型double, 字符型char, 短整型short等等。用这些基本数据类型声明变量通常是这样：

char a; //变量a的类型均为字符型char
char letter;
int x,
y,
z; //变量x,y和z的类型均为整型int
int number;
double m, n;
double result; //变量result的类型为双精度浮点型double
既然枚举也是一种数据类型，那么它和基本数据类型一样也可以对变量进行声明。

方法一：枚举类型的定义和变量的声明分开

enum DAY
{
MON=1, TUE, WED, THU, FRI, SAT, SUN
};
enum DAY yesterday;
enum DAY today;
enum DAY tomorrow; //变量tomorrow的类型为枚举型enum DAY
enum DAY good_day, bad_day; //变量good_day和bad_day的类型均为枚举型enum DAY
方法二：类型定义与变量声明同时进行：

enum //跟第一个定义不同的是，此处的标号DAY省略，这是允许的。
{
saturday,
sunday = 0,
monday,
tuesday,
wednesday,
thursday,
friday
} workday; //变量workday的类型为枚举型enum DAY
enum week { Mon=1, Tue, Wed, Thu, Fri Sat, Sun} days; //变量days的类型为枚举型enum week
enum BOOLEAN { false, true } end_flag, match_flag; //定义枚举类型并声明了两个枚举型变量
方法三：用typedef关键字将枚举类型定义成别名，并利用该别名进行变量声明：

typedef enum workday
{
saturday,
sunday = 0,
monday,
tuesday,
wednesday,
thursday,
friday
} workday; //此处的workday为枚举型enum workday的别名
workday today, tomorrow; //变量today和tomorrow的类型为枚举型workday，也即enum workday
enum workday中的workday可以省略：

typedef enum
{
saturday,
sunday = 0,
monday,
tuesday,
wednesday,
thursday,
friday
} workday; //此处的workday为枚举型enum workday的别名

workday today, tomorrow; //变量today和tomorrow的类型为枚举型workday，也即enum workday
也可以用这种方式：

typedef enum workday
{
saturday,
sunday = 0,
monday,
tuesday,
wednesday,
thursday,
friday
};

workday today, tomorrow; //变量today和tomorrow的类型为枚举型workday，也即enum workday
注意：同一个程序中不能定义同名的枚举类型，不同的枚举类型中也不能存在同名的命名常量。错误示例如下所示：

错误声明一：存在同名的枚举类型

typedef enum
{
wednesday,
thursday,
friday
} workday;

typedef enum WEEK
{
saturday,
sunday = 0,
monday,
} workday;

错误声明二：存在同名的枚举成员

typedef enum
{
wednesday,
thursday,
friday
} workday_1;

typedef enum WEEK
{
wednesday,
sunday = 0,
monday,
} workday_2;

3. 使用枚举类型的变量

3.1 对枚举型的变量赋值。

实例将枚举类型的赋值与基本数据类型的赋值进行了对比：

方法一：先声明变量，再对变量赋值

#include<stdio.h>

/* 定义枚举类型 */
enum DAY { MON=1, TUE, WED, THU, FRI, SAT, SUN };

void main()
{
/* 使用基本数据类型声明变量，然后对变量赋值 */
int x, y, z;

x = 10;
y = 20;
z = 30;

/* 使用枚举类型声明变量，再对枚举型变量赋值 */
enum DAY yesterday, today, tomorrow;

yesterday = MON;
today     = TUE;
tomorrow  = WED;

printf("%d %d %d \n", yesterday, today, tomorrow);

}
方法二：声明变量的同时赋初值

#include <stdio.h>

/* 定义枚举类型 */
enum DAY { MON=1, TUE, WED, THU, FRI, SAT, SUN };

void main()
{
/* 使用基本数据类型声明变量同时对变量赋初值 */
int x=10, y=20, z=30;

/* 使用枚举类型声明变量同时对枚举型变量赋初值 */
enum DAY yesterday = MON, 
                    today = TUE,
               tomorrow = WED;

printf("%d %d %d \n", yesterday, today, tomorrow);

}
方法三：定义类型的同时声明变量，然后对变量赋值。

#include <stdio.h>

/* 定义枚举类型，同时声明该类型的三个变量，它们都为全局变量 */
enum DAY { MON=1, TUE, WED, THU, FRI, SAT, SUN } yesterday, today, tomorrow;

/* 定义三个具有基本数据类型的变量，它们都为全局变量 */
int x, y, z;

void main()
{
/* 对基本数据类型的变量赋值 */
x = 10; y = 20; z = 30;

/* 对枚举型的变量赋值 */
yesterday = MON;
today     = TUE;
tomorrow  = WED;

printf("%d %d %d \n", x, y, z); //输出：10 20 30
printf("%d %d %d \n", yesterday, today, tomorrow); //输出：1 2 3

}
方法四：类型定义，变量声明，赋初值同时进行。

#include <stdio.h>

/* 定义枚举类型，同时声明该类型的三个变量，并赋初值。它们都为全局变量 */
enum DAY
{
MON=1,
TUE,
WED,
THU,
FRI,
SAT,
SUN
}
yesterday = MON, today = TUE, tomorrow = WED;

/* 定义三个具有基本数据类型的变量，并赋初值。它们都为全局变量 */
int x = 10, y = 20, z = 30;

void main()
{
printf(“%d %d %d \n”, x, y, z); //输出：10 20 30
printf(“%d %d %d \n”, yesterday, today, tomorrow); //输出：1 2 3
}

3.2 对枚举型的变量赋整数值时，需要进行类型转换。

#include <stdio.h>

enum DAY { MON=1, TUE, WED, THU, FRI, SAT, SUN };

void main()
{
enum DAY yesterday, today, tomorrow;

yesterday = TUE;
today = (enum DAY) (yesterday + 1); //类型转换
tomorrow = (enum DAY) 30; //类型转换
//tomorrow = 3; //错误

printf("%d %d %d \n", yesterday, today, tomorrow); //输出：2 3 30

}

3.3 使用枚举型变量

#include<stdio.h>

enum
{
BELL = ‘\a’,
BACKSPACE = ‘\b’,
HTAB = ‘\t’,
RETURN = ‘\r’,
NEWLINE = ‘\n’,
VTAB = ‘\v’,
SPACE = ’ ’
};

enum BOOLEAN { FALSE = 0, TRUE } match_flag;

void main()
{
int index = 0;
int count_of_letter = 0;
int count_of_space = 0;

char str[] = "I'm Ely efod";

match_flag = FALSE;

for(; str[index] != '\0'; index++)
    if( SPACE != str[index] )
        count_of_letter++;
    else
    {
        match_flag = (enum BOOLEAN) 1;
        count_of_space++;
    }

printf("%s %d times %c", match_flag ? "match" : "not match", count_of_space, NEWLINE);
printf("count of letters: %d %c%c", count_of_letter, NEWLINE, RETURN);

}
输出：
match 2 times
count of letters: 10
Press any key to continue

4. 枚举类型与sizeof运算符

#include <stdio.h>

enum escapes
{
BELL = ‘\a’,
BACKSPACE = ‘\b’,
HTAB = ‘\t’,
RETURN = ‘\r’,
NEWLINE = ‘\n’,
VTAB = ‘\v’,
SPACE = ’ ’
};

enum BOOLEAN { FALSE = 0, TRUE } match_flag;

void main()
{
printf(“%d bytes \n”, sizeof(enum escapes)); //4 bytes
printf(“%d bytes \n”, sizeof(escapes)); //4 bytes

printf("%d bytes \n", sizeof(enum BOOLEAN)); //4 bytes
printf("%d bytes \n", sizeof(BOOLEAN)); //4 bytes
printf("%d bytes \n", sizeof(match_flag)); //4 bytes

printf("%d bytes \n", sizeof(SPACE)); //4 bytes
printf("%d bytes \n", sizeof(NEWLINE)); //4 bytes
printf("%d bytes \n", sizeof(FALSE)); //4 bytes
printf("%d bytes \n", sizeof(0)); //4 bytes

}

5. 综合举例

#include<stdio.h>

enum Season
{
spring, summer=100, fall=96, winter
};

typedef enum
{
Monday, Tuesday, Wednesday, Thursday, Friday, Saturday, Sunday
}
Weekday;

void main()
{
/* Season */
printf(“%d \n”, spring); // 0
printf(“%d, %c \n”, summer, summer); // 100, d
printf(“%d \n”, fall+winter); // 193

Season mySeason=winter;
if(winter==mySeason)
    printf("mySeason is winter \n"); // mySeason is winter

int x=100;
if(x==summer)
    printf("x is equal to summer\n"); // x is equal to summer

printf("%d bytes\n", sizeof(spring)); // 4 bytes

/* Weekday */
printf("sizeof Weekday is: %d \n", sizeof(Weekday)); //sizeof Weekday is: 4

Weekday today = Saturday;
Weekday tomorrow;
if(today == Monday)
    tomorrow = Tuesday;
else
    tomorrow = (Weekday) (today + 1); //remember to convert from int to Weekday

}