Leetcode
- Leetcode -637.二叉树的层平均值
- Leetcode -671.二叉树中第二小的节点
Leetcode -637.二叉树的层平均值
题目:给定一个非空二叉树的根节点 root , 以数组的形式返回每一层节点的平均值。与实际答案相差 10^(- 5) 以内的答案可以被接受。
示例 1:
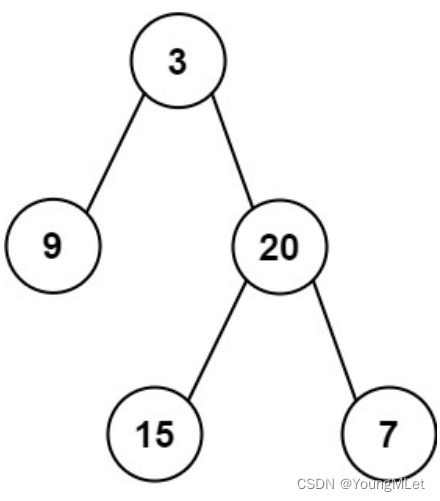
输入:root = [3, 9, 20, null, null, 15, 7]
输出:[3.00000, 14.50000, 11.00000]
解释:第 0 层的平均值为 3, 第 1 层的平均值为 14.5, 第 2 层的平均值为 11 。
因此返回[3, 14.5, 11] 。
示例 2:
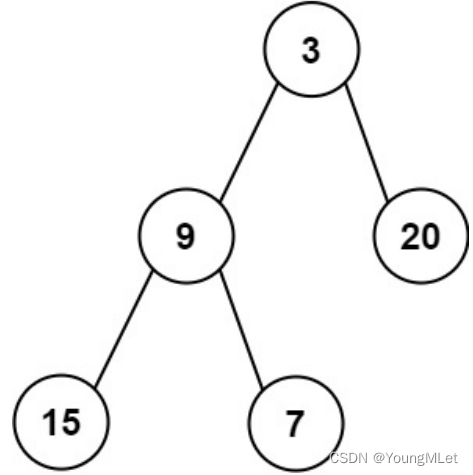
输入:root = [3, 9, 20, 15, 7]
输出:[3.00000, 14.50000, 11.00000]
提示:
树中节点数量在 [1, 104] 范围内
- 2^31 <= Node.val <= 2^31 - 1
思路:一共要创建三个数组,SumVal 数组记录每一层的节点的和;CountLevels 数组记录每一层的节点数;ret 数组记录每一层的平均值,即利用前两个数组计算后放到 ret 数组中,最后返回;
void dfs(struct TreeNode* root, double* SumVal, int* CountLevels, int level, int* posSumSize, int* posCountSize)
{
if (root == NULL)
return;
// level 是记录当前节点所在的层数
if (level < *posSumSize)
{
SumVal[level] += (double)root->val;
CountLevels[level] += 1;
}
//每次递归到新的一层,就会将最左边的节点的值累加到下标为 posSumSize 位置的 SumVal 数组中
//并将 CountLevels 数组中下标为 posCountSize 的位置置1
else
{
SumVal[(*posSumSize)++] = (double)root->val;
CountLevels[(*posCountSize)++] = 1;
}
//递归其左子树和右子树,层数加一
dfs(root->left, SumVal, CountLevels, level + 1, posSumSize, posCountSize);
dfs(root->right, SumVal, CountLevels, level + 1, posSumSize, posCountSize);
}
double* averageOfLevels(struct TreeNode* root, int* returnSize)
{
//SumVal 数组存放每一层的节点和;CountLevels 数组存放每一层的节点数
double* SumVal = (double*)malloc(sizeof(double) * 10000);
int* CountLevels = (int*)malloc(sizeof(int) * 10000);
//posSumSize 和 posCountSize 分别记录两个数组的长度
int posSumSize = 0, posCountSize = 0;
//深度优先搜索
dfs(root, SumVal, CountLevels, 0, &posSumSize, &posCountSize);
//返回数组的长度
*returnSize = posSumSize;
//ret 数组存放每一层的平均值
double* ret = (double*)malloc(sizeof(double) * posSumSize);
for (int i = 0; i < posSumSize; i++)
{
ret[i] = SumVal[i] / CountLevels[i];
}
return ret;
}
Leetcode -671.二叉树中第二小的节点
题目:给定一个非空特殊的二叉树,每个节点都是正数,并且每个节点的子节点数量只能为 2 或 0。如果一个节点有两个子节点的话,那么该节点的值等于两个子节点中较小的一个。
更正式地说,即 root.val = min(root.left.val, root.right.val) 总成立。
给出这样的一个二叉树,你需要输出所有节点中的 第二小的值 。
如果第二小的值不存在的话,输出 - 1 。
示例 1:
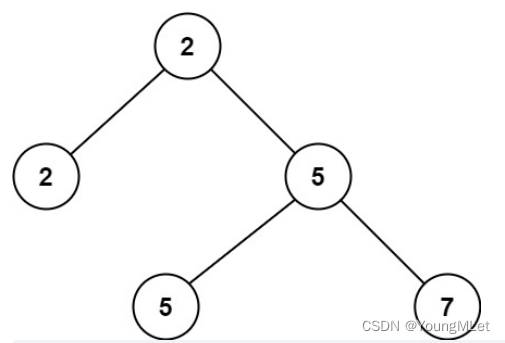
输入:root = [2, 2, 5, null, null, 5, 7]
输出:5
解释:最小的值是 2 ,第二小的值是 5 。
示例 2:
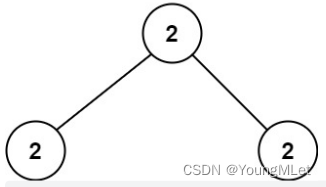
输入:root = [2, 2, 2]
输出: - 1
解释:最小的值是 2, 但是不存在第二小的值。
提示:
树中节点数目在范围[1, 25] 内
1 <= Node.val <= 2^31 - 1
对于树中每个节点 root.val == min(root.left.val, root.right.val)
思路:因为树中的每个节点都满足 root.val == min(root.left.val, root.right.val);所以根节点就是最小的节点,我们即需要找到比根节点大的节点中最小的节点就是树中第二小的节点;
void dfs(struct TreeNode* root, int* ret, int rootval)
{
if (root == NULL)
return;
//如果 ret 已被更改,且当前节点的值大于当前 ret 的值,就返回
//因为 ret 要找的是比根节点大的值中最小的值
if (*ret != -1 && root->val >= *ret)
return;
// rootval 是根节点的值,根节点就是最小的值,找出比它大的数中最小的那个即可
// 如果节点的值比当前 ret 大,会在上面直接返回
if (root->val > rootval)
*ret = root->val;
//递归其左子树和右子树
dfs(root->left, ret, rootval);
dfs(root->right, ret, rootval);
}
int findSecondMinimumValue(struct TreeNode* root)
{
//返回值初始化为 -1
int ret = -1;
dfs(root, &ret, root->val);
return ret;
}