一、简介

ECDH全称是椭圆曲线迪菲-赫尔曼秘钥交换（Elliptic Curve Diffie–Hellman key Exchange），主要是用来在一个不安全的通道中建立起安全的共有加密资料，一般来说交换的都是私钥，这个密钥一般作为“对称加密”的密钥而被双方在后续数据传输中使用。

ECDH是建立在这样一个前提之上的，给定椭圆曲线上的一个点P，一个整数k，求Q=KP很容易；但是通过Q，P求解K很难。

二、DH密钥交换原理

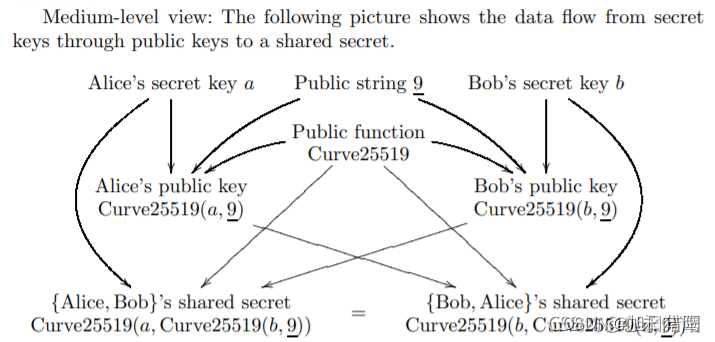
网上一个经典的场景，Alice和Bob要在一条不安全的线路上交换秘钥，交换的秘钥不能被中间人知晓。
首先，双方约定使用ECDH秘钥交换算法，这个时候双方也知道了ECDH算法里的一个大素数P，这个P可以看做是一个算法中的常量。

P的位数决定了攻击者破解的难度

还有一个整数g用来辅助整个秘钥交换，g不用很大，一般是2或者5，双方知道g和p之后就开始了ECDH交换秘钥的过程了。

Alice知道了共用参数p和g，生成私有整数a作为私钥，公钥算法一般是公钥加密，私钥解密，公钥给对方来加密数据，拿到密文后私钥解密查看内容正确性，这个时候Alice直接通过线路告诉Bob自己的私钥a显然既不合理也是一件风险很大的事。 这个时候Alice需要利用p，g，a通过公式$g^{a}modp=A$生成A作为公钥传递。

Bob通过链路收到Alice发来的p，g，A，知道了Alice的公钥A。这个时候Bob也生成自己的私钥b，然后通过公式$g^{b}modp=B$生成自己公钥B。 在发送公钥B前，Bob通过$A^{b}modp=K$生成K作为公共秘钥，但是并不发送给Alice，只通过链路发送B。

Alice收到Bob发来的公钥B以后，同样通过$B^{a}modp=K$生成公共秘钥K，这样Alice和Bob就通过不传递私钥a和b完成了对公共秘钥K的协商。

三、说明示例

1. Alice和Bob同意使用质数p和整数g：

$p=83,g=8$

2. Alice选择秘钥 $a=9$, 生成公钥 $g^{a}modp=A$ 并发送

$(8^9)mod83=5$

3. Bob选择秘钥 $b=21$, 生成公钥 $g^b mod p = B $并发送

$(8^{2}1)mod83=18$

4. Alice计算 $B^{a}modp=K$

$18^{9}mod83=24$

5. Bob计算 $B^{a}modp=K$

$5^{2}1mod83=24$

至此24就是双方协商出来的秘钥。