题目大意：
东海岸有N个城市，西海岸有M个城市（N≤1000，M≤1000），将建K条公路。每个海岸的城市从北到南编号为1,2，…每条高速公路都是直线，连接东海岸和西海岸的城市。建设资金由高速公路之间的交叉数决定。两个高速公路最多在一个地方交叉。请计算告诉公路之间的交叉数量。

输入：
输入以T开始，表示测试用例的数量。
每个测试用例都是3个整数N、M、K。
下面的K行每一行都包含两个数字，表示高速公路连接的城市号。第一个数是东海岸的城市号，第二个数字是西海岸的城市号。

输出：
对每个测试用例都输出“Test case x:s”，x表示输入样例编号，s表示交叉数。

输入样例：
1
3 4 4
1 4
2 3
3 2
3 1
输出样例：
Test case 1:5

题解：
根据样例，一共有5个交叉点，如下图

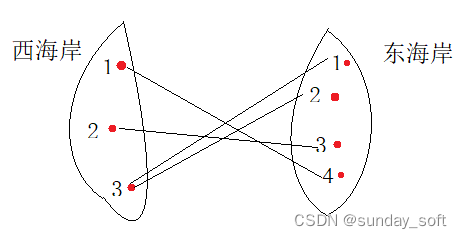
我们探讨一下怎么产生的交叉点，如果两边的城市都是以升序（降序）出现，我们发现就不会产生交叉点。
例如，1 2 和 2 3 就不会产生交叉点。

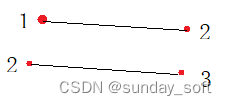
1 4 2 3就会产生交叉点，因为西海岸城市1、2是升序的，东海岸城市4、3是降序的。因此产生交叉和逆序对有关系。

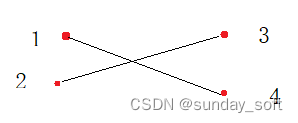
通过上面分析，求交叉的数量，就是把公路两端的城市号，一端升序排列，另一端求逆序对的个数。

算法设计：
1、对数的边按照x升序排列，若x相等，则按有升序排列。
2、检查每条边i，统计y的前缀和sum（e[i].y）,该前缀和是前面比y小的正序数，即可得到逆序数为i-sum（e[i].y)，也就是前面的边和第i条边产生交叉的个数，ans累加这个交叉个数。
3、将树状数组中的e[i].y的值加1。

算法图解：
1、对边排序结果：
1 4
2 3
3 1
3 2

2、按照排序结果检查每条边i，统计y的前缀和sum（e[i].y），将ans累加i-sum（e[i].y）。
i=0： 1 4，sum（4）=0，i-sum（4）=0；4的前缀和为0，说明4前面没有比4小的数，因为前面还没有边，所以逆序对ans=0。

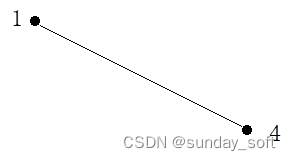
i=1： 2 3，sum（3）=0，i-sum（0）=1。3的前缀和为0，说明3前面没有数，所以前面的1条边是逆序的，当前边和逆序边会产生交点，累加逆序边数量ans=1。
（sum（）始终是统计的正序数）。

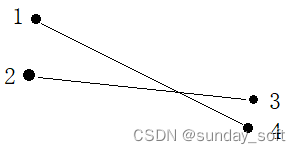
i=2： 3 1。sum（1）=0，i-sum（1）=2。1的前缀和为0，说明1前面没有正序数（也就是比1小的数），因此前面出现的两条边都是逆序的，当前边和每条逆序边会产生交点。累加逆序边数量ans=3

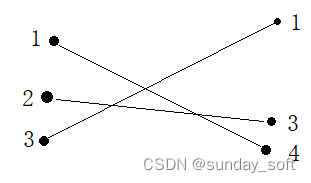
i=3： 3 2。sum（2）=1，i-sum（2）=2；前面的三条边已经有1条边是正序的，将该边减去，其余两条边是逆序的，当前边和每个逆序边会产生交点，累加逆序边数量ans=5。

代码如下：

#include<cstdio>
#include<cstring>
#include<algorithm>
#define maxn 1010
#define maxk 1000010
#define lowbit(x) (x)&(-x)
int c[maxn],kas,n,m,k;
using namespace std;
typedef long long LL;
struct Edge {
    int x, y;
}e[maxk];
bool cmp(Edge a,Edge b)
{
    return a.x<b.x||(a.x==b.x&&a.y<b.y);
}

void add(int i)//加1操作，参数省略
{
    while(i<=m)//y点有m个
	{
        ++c[i];
        i+=lowbit(i);
    }
}

int sum(int i)
{
    int s=0;
    while(i>0)
	{
        s+=c[i];
        i-=lowbit(i);
    }
    return s;
}

int main()
{
    int T;
    scanf("%d",&T);
    while (T--)
	{
		memset(c,0,sizeof(c));
	    scanf("%d%d%d",&n,&m,&k);
	    for(int i=0;i<k;i++)
			scanf("%d%d",&e[i].x,&e[i].y);
	    sort(e,e+k,cmp);
	    LL ans=0;
	    for(int i=0;i<k;i++){
	        ans+=i-sum(e[i].y);
	        add(e[i].y);
			/*
			表示以y端点的边出现一次，更新c[y],利用树状数组机制，更新后面
			关联的c[ ],表示后面比y大的数正序数都会增加1。
			c[y]先使用，后更新,主要是为更新比y大的数， 
			*/ 
	    }
	    printf("Test case %d: %lld\n",++kas,ans);
	}
    return 0;
}