💓博主CSDN主页:杭电码农-NEO💓
 
⏩专栏分类:八大排序专栏⏪
 
🚚代码仓库:NEO的学习日记🚚
 
🌹关注我🫵带你学习排序知识
  🔝🔝

---

---

1. 前言

比较八大排序不能直接将
这八个排序放在一起讨论
我们根据大致效率将它们分为两组:
(每个排序的详情链接在后面)

1. 第一组

• 插入排序 详情
• 选择排序 详情
• 冒泡排序 (略)

2. 第二组

• 堆排序 详情
• 希尔排序 详情
• 快速排序 详情
• 归并排序 详情

各大排序的进阶版本被放在了专栏:
    八大排序专栏

本篇文章将从稳定性和效率两个方面
来分析这两组排序

---

2. 什么是排序算法的稳定性?

官方话语是这样的:

排序序列中,有多个具有相同关键字的记录经过排序,记录对应的相对次序保持不变,这就是排序的稳定性。

举个例子,定义一个无序数组:

int a[]={5(i),3,6,4,5(j),2,8};

数组中有两个5
把第一个5记为 i
第二个5记为 j
当我们用任意算法排好序后

int a[]={2,3,4,5,5,6,8};//排好序后的数组

若 i 还在 j 前面,则这个算法是稳定的

int a[]={2,3,4,i,j,6,8};

若 i 在 j 后面,则算法不稳定

int a[]={2,3,4,j,i,6,8};

---

3. 各大排序稳定性分析

想要搞清楚排序是否稳定
就要明白内部的实现思路!

---

3.1 插入和希尔排序的分析

1. 插入排序:

插入排序是从数组中第一个元素开始
一一和它后面的元素做比较
并且一个元素向前挪动停下来的条件是:
当前元素的值大于等于正在挪动的元素

结论: 是稳定的

2. 希尔排序:

虽然希尔排序是对插入排序的优化
但是希尔排序多了一个分组预排序
当相同的数组被分到同一组时
它们的顺序不会变化
但是当相同的数据分到不同组时
排好序后的顺序就有可能改变!

结论: 不是稳定的

---

3.2 选择,堆排序的分析

1. 选择排序:

选择排序明显是不稳定的
当前循环选出的最大值是
这个值第一次出现的位置
将它放在数组最后,第二层循环
寻找次大值时若和刚刚的值相同
这个次打值就到倒数第二个位置了

结论: 不稳定的

2. 堆排序:

堆排序和选择排序类似
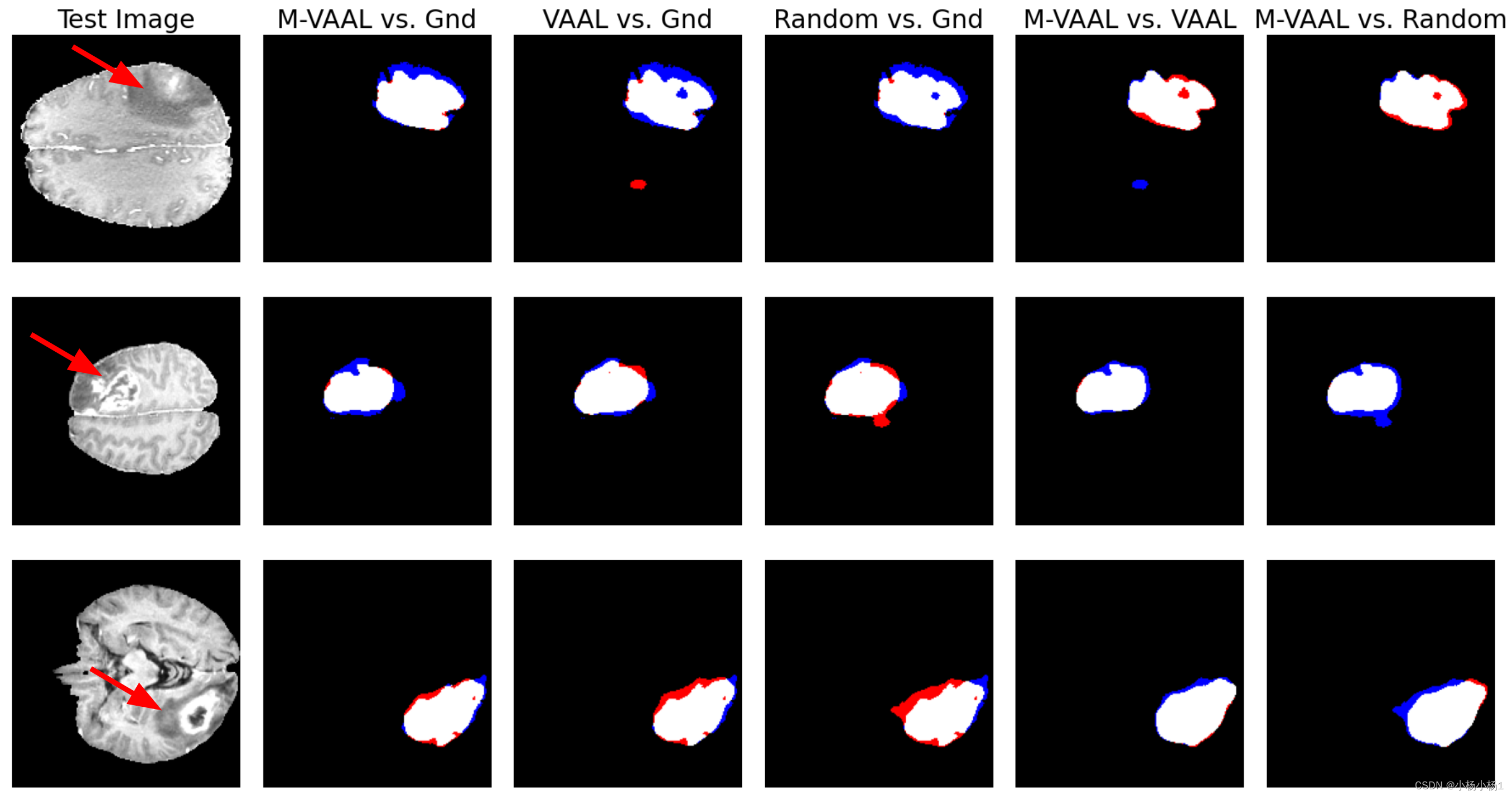
我们直接举个向下调整的例子:

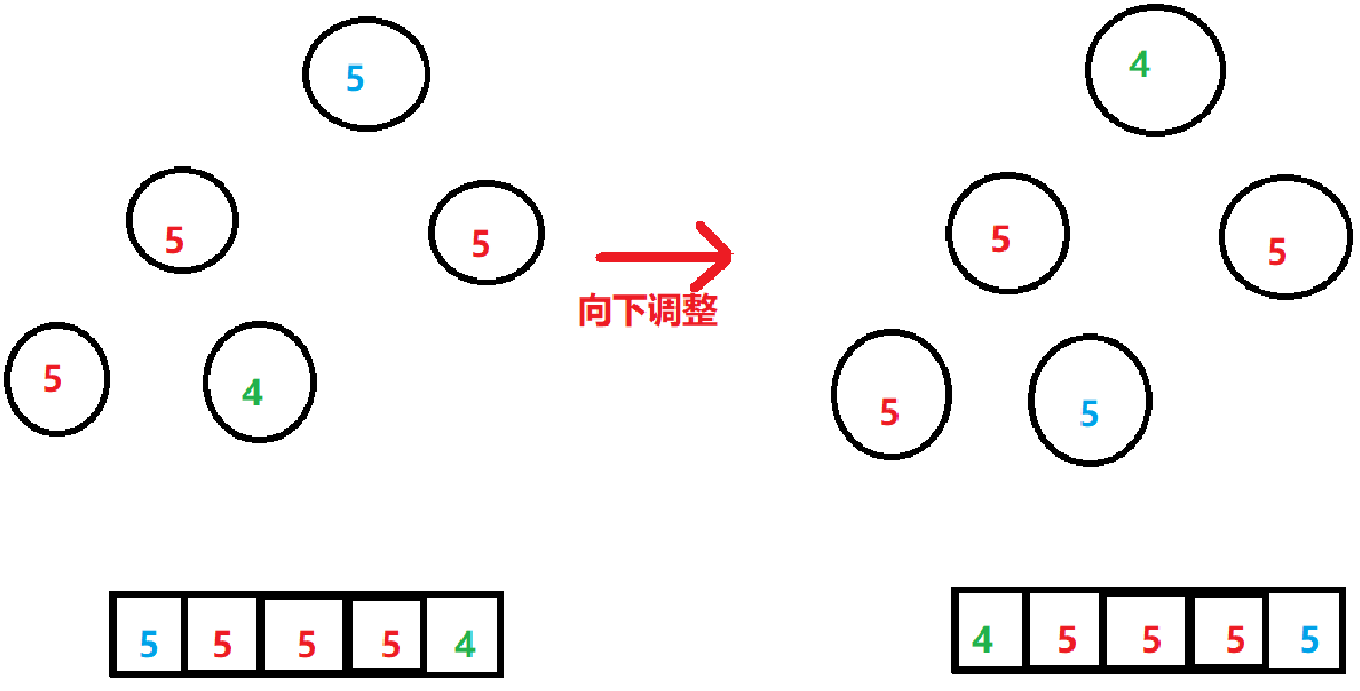
蓝色的5从第一个位置跑到最后一个了

结论: 不稳定的

---

3.3 冒泡,快速排序的分析

1. 冒泡排序:

冒泡排序是挨个儿比较
挨个儿交换.所以不会将相同的值
交换到不同的位置

结论: 稳定的

2. 快速排序

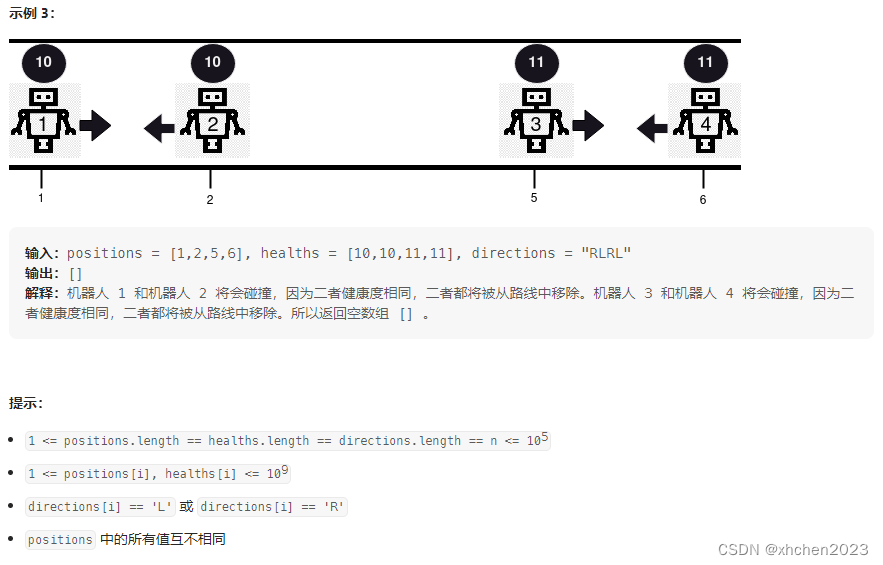
快速排序比较特殊.
当基准值key和L,R指针相遇的点
对应的值相同时,会改变位置!
画图说明:

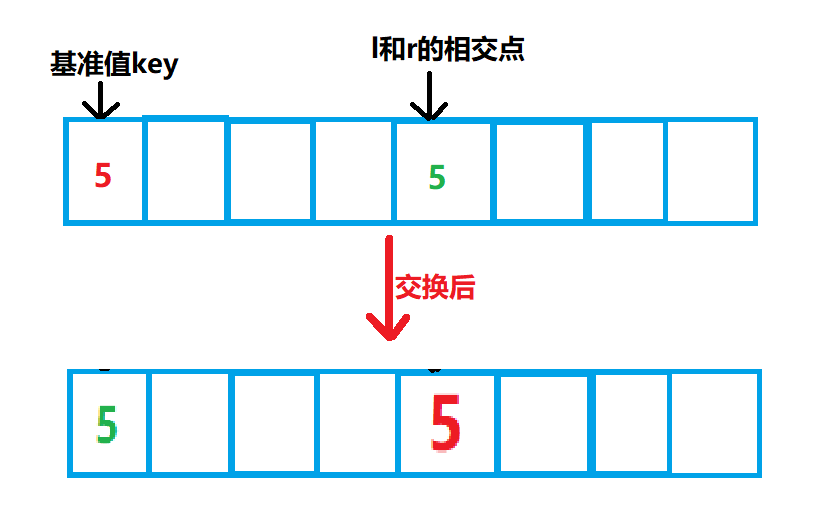
5的前后顺序发生了变化

结论: 不稳定的

---

3.4 归并排序分析

归并排序可以稳定也可以不稳定
当左右子数组中出现相同值时
如果先将左子数组的数据入数组
那么归并排序就是稳定的
如果先将右子数组的数据入数组
那么归并排序就是不稳定的

所以我们写归并排序时
数据相同时尽量先下左边

结论: 稳定的!

---

4. 各大算法效率比较

现实生活中处理的信息量往往非常大
这里我们随机生成五百万个数排序
试一试每一个排序算法要花多少毫秒?

注:clock是记录程序
走到当前这一行运行的时长
两个clock相减就是中间程序运行的时间

//测试性能
void TestOP()
{
	srand(time(0));
	const int N = 5000000;
	int* a1 = (int*)malloc(sizeof(int) * N);
	int* a2 = (int*)malloc(sizeof(int) * N);
	int* a3 = (int*)malloc(sizeof(int) * N);
	int* a4 = (int*)malloc(sizeof(int) * N);
	int* a5 = (int*)malloc(sizeof(int) * N);
	int* a6 = (int*)malloc(sizeof(int) * N);
	int* a7 = (int*)malloc(sizeof(int) * N);

	for (int i = 0; i < N; ++i)
	{
		a1[i] = rand();
		a2[i] = a1[i];
		a3[i] = a1[i];
		a4[i] = a1[i];
		a5[i] = a1[i];
		a6[i] = a1[i];
	}

	int begin1 = clock();
	InsertSort(a2, N);
	int end1 = clock();

	int begin2 = clock();
	ShellSort(a2, N);
	int end2 = clock();

	int begin3 = clock();
	SelectSort(a3, N);
	int end3 = clock();

	int begin4 = clock();
	HeapSort(a2, N);
	int end4 = clock();

	int begin5 = clock();
	QuickSort(a2, 0, N - 1);
	QuickSort(a2, 0, N - 1);
	int end5 = clock();

	int begin6 = clock();
	MergeSort(a2, N);
	int end6 = clock();

	printf("InsertSort:%d ms\n", end1 - begin1);
	printf("ShellSort:%d ms\n", end2 - begin2);
	printf("SelectSort:%d ms\n", end3 - begin3);
	printf("HeapSort:%d ms\n", end4 - begin4);
	printf("QuickSort:%d ms\n", end5 - begin5);
	printf("MergeSort:%d ms\n", end6 - begin6);

	free(a1);
	free(a2);
	free(a3);
	free(a4);
	free(a5);
	free(a6);
}

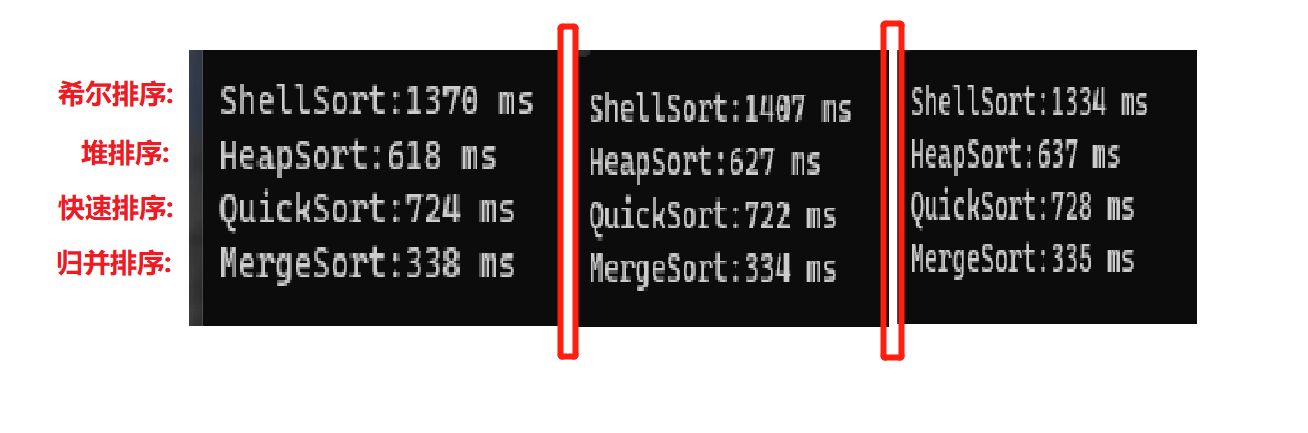
对于五百万个数据来说
插入,选择,冒泡排序运行的时间会很长
所以我们这里直接比较第二组排序:

五百万个数据:

一百万个数据:

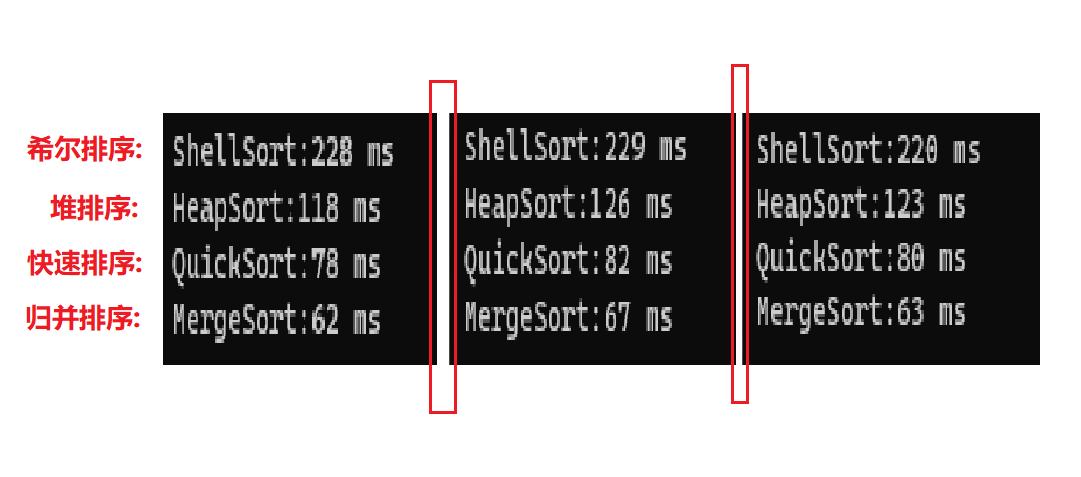
每个排序效率都不错
快排与归并格外的好!

---

5. 总结与代码分享

八大排序整体完结!
下面分享一个知识表格大全:

排序方法	最好情况	最坏情况	辅助空间	稳定性
冒泡排序	O(N)	O(N2)	O(1)	稳定
选择排序	O(N2	O(N2	O(1)	不稳定
插入排序	O(N)	O(N2	O(1)	稳定
希尔排序	O(N1.3)	O(N2)	O(1)	不稳定
堆排序	O(N*log2N)	O(N*log2N)	O(N)	不稳定
快速排序	O(N*log2N)	O(N2)	O(log2N~N)	不稳定
归并排序	O(N*log2N)	O(N*log2N)	O(N)	稳定

我将C语言实现八大排序
所有代码汇总分享给大家:

gitee代码仓库

八大排序所有内容结束!

🔎 下期预告:C嘎嘎初阶 🔍