A 美丽下标对的数目
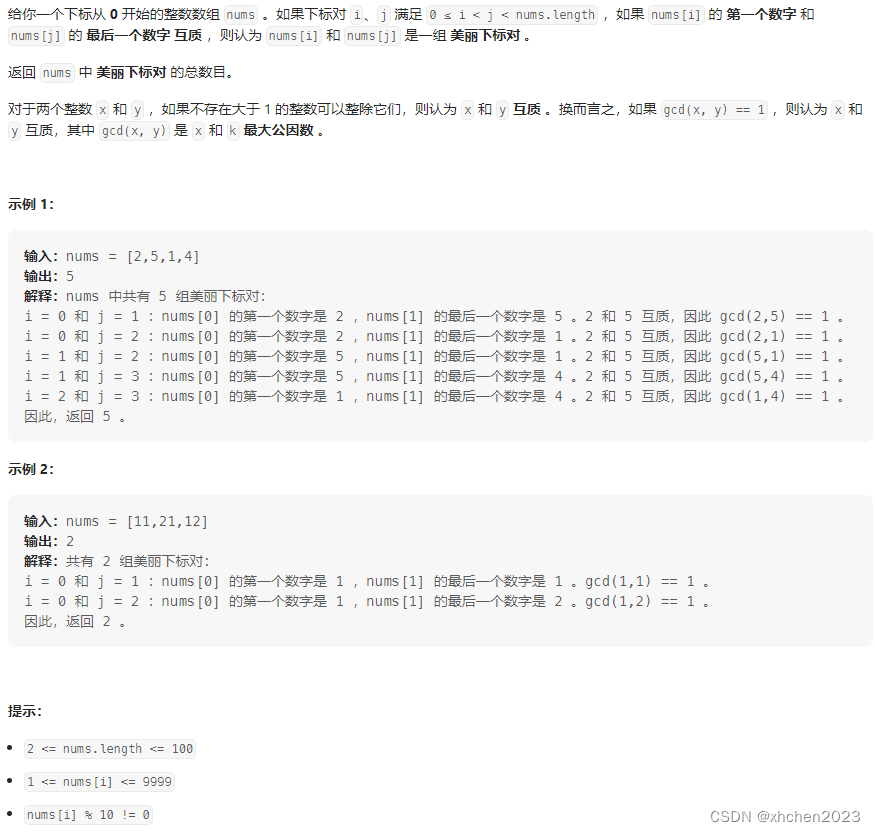
模拟
class Solution {
public:
int countBeautifulPairs(vector<int> &nums) {
int n = nums.size();
int res = 0;
for (int i = 0; i < n; i++)
for (int j = i + 1; j < n; j++)
if (gcd(to_string(nums[i])[0] - '0', to_string(nums[j]).back() - '0') == 1)
res++;
return res;
}
};
B 得到整数零需要执行的最少操作数
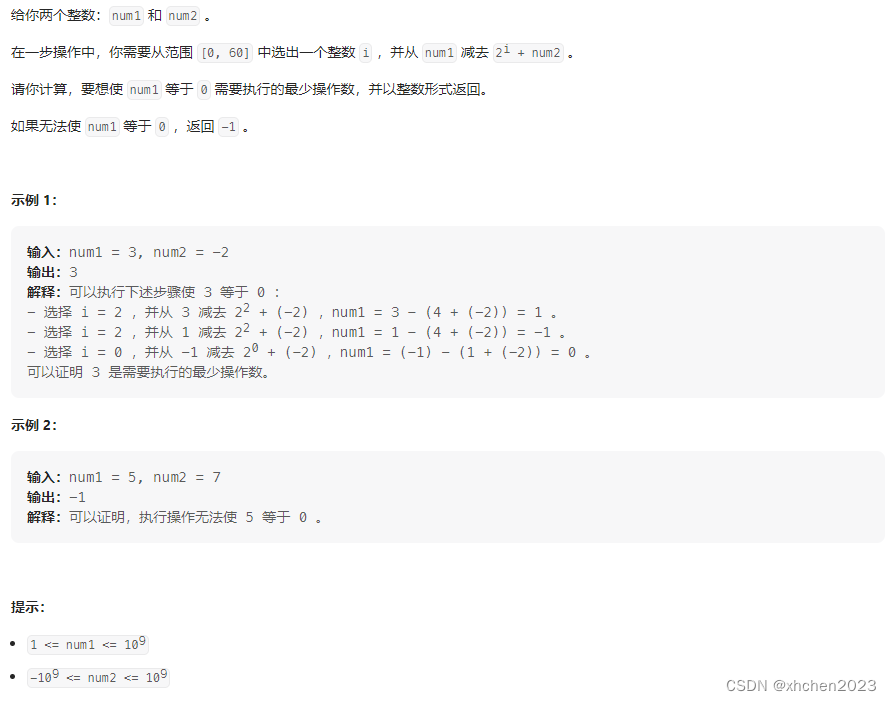
脑筋急转弯:考虑 r = n u m 1 − k × n u m 2 r=num_1-k\times num_2 r=num1−k×num2,若 r ≥ k r\ge k r≥k(执行 k k k次操作后可以使 n u m 1 num1 num1非负), 且 r r r的二进制中1的个数 ≤ k \le k ≤k, 则可以把 r r r拆分成 k k k个2的非负整数幂与前面减去的 k k k个 n u m 2 num_2 num2分别配对, 即存在操作次数为 k k k的方案.
class Solution {
public:
typedef long long ll;
int popcnt(ll x) {// 计算2进制中1的个数
int res = 0;
for (; x; x >>= 1)
if (x & 1)
res++;
return res;
}
int makeTheIntegerZero(int num1, int num2) {
int res = INT32_MAX;
ll a = num1, b = num2;
for (int k = 1; k <= 35; k++) {
if (a - (b * k + k) >= 0 && popcnt(a - b * k) <= k)
res = min(res, k);
}
return res == INT32_MAX ? -1 : res;
}
};
C 将数组划分成若干好子数组的方式

动态规划: 定义 p i p_i pi为将 n u m s [ 0 ∼ i − 1 ] nums[0\sim i-1] nums[0∼i−1]划分成若干好子数组的方式数, 若 n u m s [ i − 1 ] = = 0 nums[i-1]==0 nums[i−1]==0, n u m s [ i − 1 ] nums[i-1] nums[i−1]只能和 n u m s [ i − 2 ] nums[i-2] nums[i−2]一组, 所以 p i = p i − 1 p_i=p_{i-1} pi=pi−1, n u m s [ i − 1 ] = = 1 nums[i-1]==1 nums[i−1]==1, 设上一个1对应的下标为last, 则有 p i = ∑ l a s t ≤ k < i p k p_i=\sum_{last\le k< i } p_k pi=∑last≤k<ipk, 实现时用前缀和计算
class Solution {
public:
typedef long long ll;
ll mod = 1e9 + 7;
int numberOfGoodSubarraySplits(vector<int> &nums) {
int n = nums.size();
ll p[n + 1];
ll pre[n + 1];
p[0] = 0;
pre[0] = 0;
for (int i = 1, last = -1; i <= n; i++) {
if (nums[i - 1] == 0)
p[i] = p[i - 1];
else {
if (last == -1)
p[i] = 1;
else
p[i] = (pre[i - 1] - pre[last - 1]) % mod;
last = i;
}
pre[i] = pre[i - 1] + p[i];
pre[i] %= mod;
}
return (p[n] % mod + mod) % mod;
}
};
D 机器人碰撞
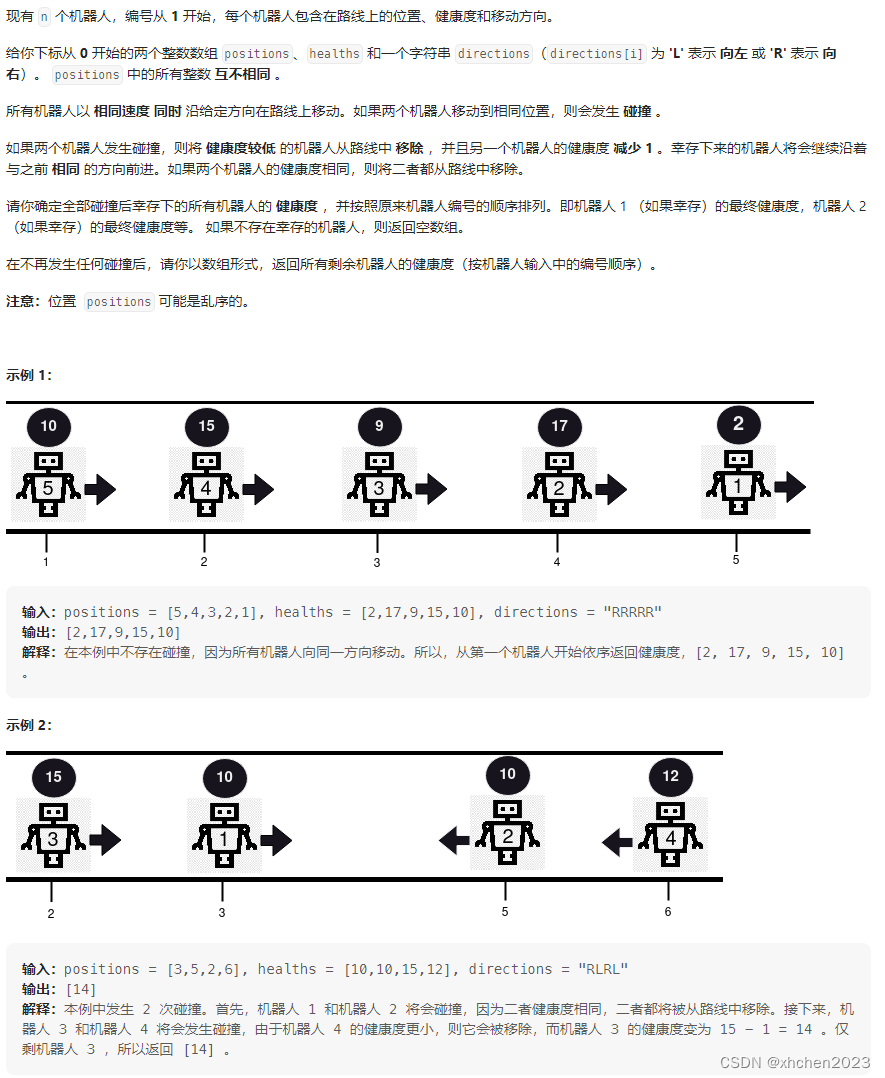
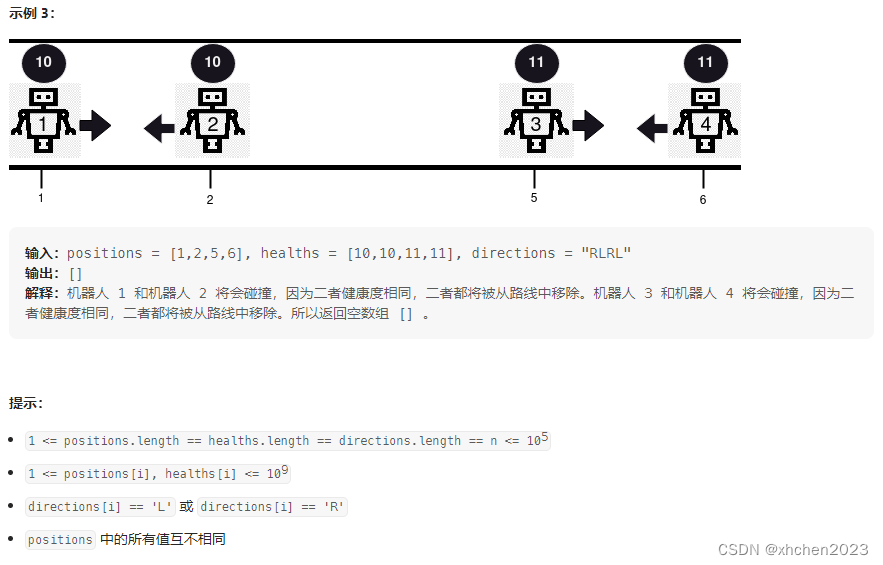
栈: 把机器人按位置升序排序, 然后顺序遍历机器人判断是否能入栈, 两个机器人碰撞的情况只能是栈尾机器人向右且当前遍历到机器人向左, 之后分类讨论处理进出栈. 遍历完后对栈中剩余机器人按原始下标排序返回剩余健康度.
class Solution {
public:
vector<int> survivedRobotsHealths(vector<int> &positions, vector<int> &healths, string directions) {
int n = positions.size();
vector<tuple<int, int, char, int>> li;//pos,heal,dir,index
for (int i = 0; i < n; i++)
li.emplace_back(positions[i], healths[i], directions[i], i);
sort(li.begin(), li.end());// 按位置升序排序
vector<tuple<int, int, char, int>> st;
for (auto &x: li) {
if (!st.empty() && get<2>(st.back()) == 'R' && get<2>(x) == 'L') {
int del_x = 0;// 是否删除当前遍历到的机器人x
while (!st.empty() && get<2>(st.back()) == 'R' && get<2>(x) == 'L') {
if (get<1>(st.back()) < get<1>(x)) {// 栈尾健康度<x健康度
st.pop_back();
get<1>(x)--;
} else if (get<1>(st.back()) > get<1>(x)) {// 栈尾健康度>x健康度
get<1>(st.back())--;
del_x = 1;
break;
} else {// 栈尾健康度==x健康度
del_x = 1;
st.pop_back();
break;
}
}
if (!del_x)
st.push_back(x);
} else
st.push_back(x);
}
sort(st.begin(), st.end(), [](auto &x, auto &y) { return get<3>(x) < get<3>(y); });//按原始下标升序排序
vector<int> res;
for (auto &x: st)
res.push_back(get<1>(x));
return res;
}
};