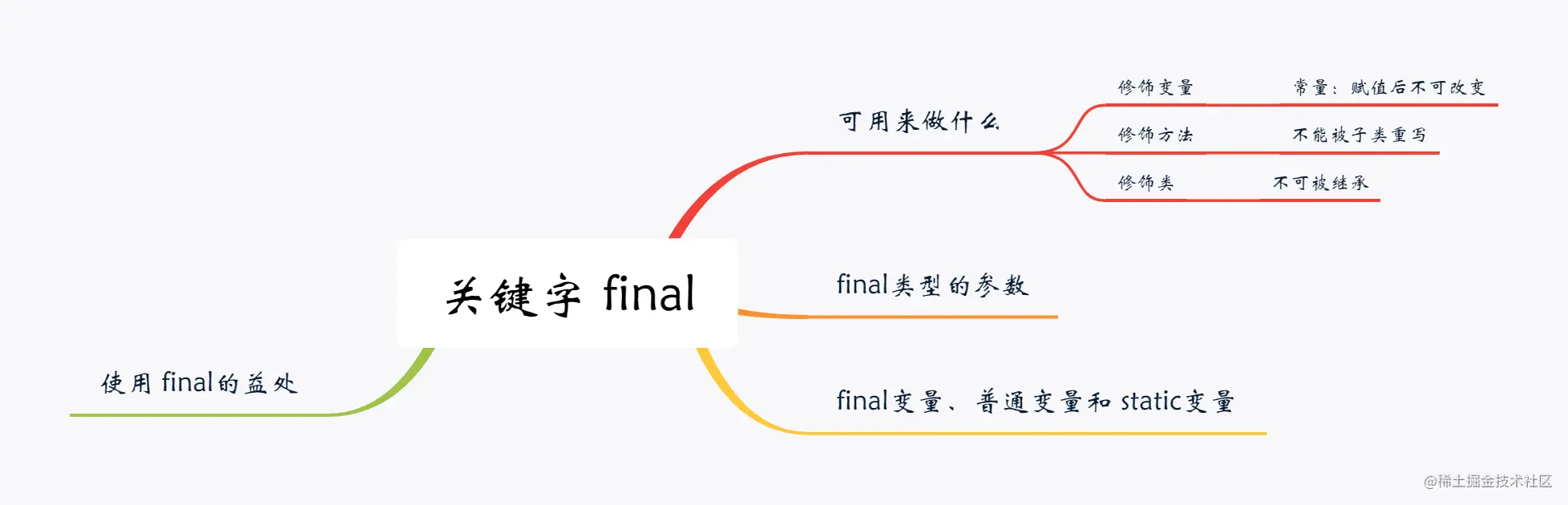
文章目录
- 1. Faiss 简介
- 2. 距离度量
- 3. 在 Sophon TPU 上的接口实现
- 3.1 Sophon TPU
- 3.2 indexflat 实现
- 3.3 indexPQ 实现
===========================================
1. Faiss 简介
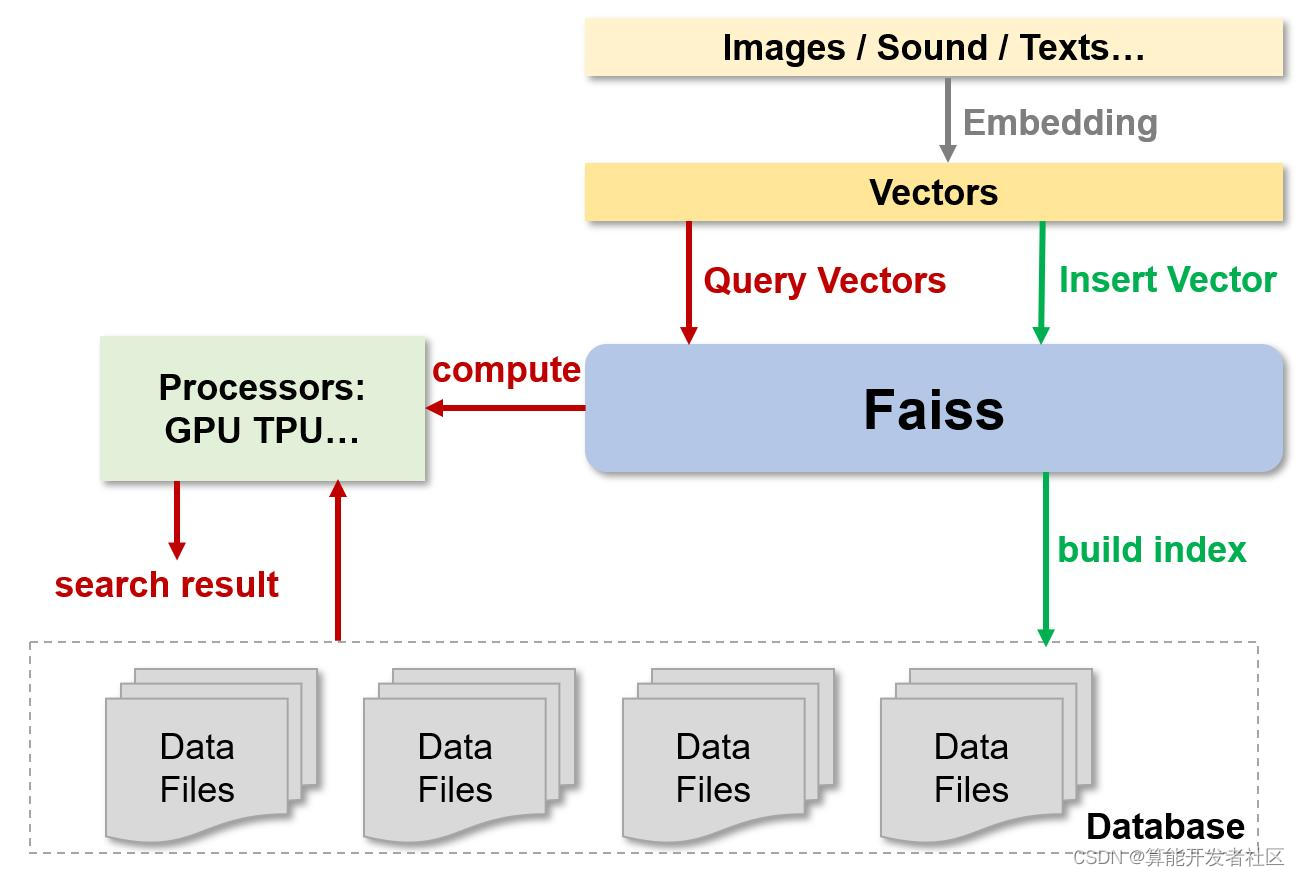
Faiss 库是 Facebook 开发的一个用于稠密向量相似性搜索和聚类的库,该库包含有诸多向量相似性搜索的算法。向量相似性搜索是将一个向量与底库中的向量集合进行比较,从中找到与检索向量最相似的向量的过程。常见的图像、音视频等均可用机器学习模型转化为嵌入向量,因此 Faiss 库在语义搜索、推荐系统等现实场景中得到了广泛的应用。
使用 Faiss 库对某一个向量进行检索,整个检索的步骤分为 train、add、search 三个步骤,首先选取具有代表性的数据训练得到索引值;然后将索引值添加到底库中;对于给定的输入检索向量,在底库中搜索最相似的
K
K
K 个向量。
2. 距离度量
那么,如何确定两个向量之间的相似性呢?
Faiss 库提供了两种常见的距离度量方法,其一是欧式距离 (Euclidean Distance),也可称为 L2 距离 (L2 Distance);其二是内积距离(Inner Product, IP)。
设特征空间
X
\mathcal{X}
X 是
n
n
n 维实数向量空间
R
n
\mathcal{R}^n
Rn,
x
,
y
∈
X
\mathbf{x},\mathbf{y}\in \mathcal{X}
x,y∈X,
x
=
(
x
1
,
x
2
,
⋯
,
x
n
)
T
\mathbf{x}=(x_1,x_2,\cdots,x_n)^T
x=(x1,x2,⋯,xn)T,
y
=
(
y
1
,
y
2
,
⋯
,
y
n
)
T
\mathbf{y}=(y_1,y_2,\cdots,y_n)^T
y=(y1,y2,⋯,yn)T,两个向量之间的夹角为
θ
\theta
θ。
x
\mathbf{x}
x 与
y
\mathbf{y}
y 之间的 L2 距离为:
L
2
(
x
,
y
)
=
∑
i
=
1
n
∣
x
i
−
y
i
∣
2
L_2(\mathbf{x},\mathbf{y})=\sqrt{\sum_{i=1}^n|x_i-y_i|^2}
L2(x,y)=i=1∑n∣xi−yi∣2
x
\mathbf{x}
x 与
y
\mathbf{y}
y 之间的内积距离为:
IP
(
x
,
y
)
=
x
⋅
y
=
∑
i
=
1
n
x
i
y
i
=
∥
x
∥
∥
y
∥
cos
θ
\text{IP}(\mathbf{x},\mathbf{y})=\mathbf{x}\cdot\mathbf{y}=\sum_{i=1}^{n}x_iy_i=\|\mathbf{x}\|\|\mathbf{y}\|\cos\theta
IP(x,y)=x⋅y=i=1∑nxiyi=∥x∥∥y∥cosθ
L2 距离值越小,表示两个向量间的相似度越高。相反,内积距离值越大,表示两个向量间的相似度越高。若
x
\mathbf{x}
x 和
y
\mathbf{y}
y 两个向量已进行归一化 (Normalization) 处理,即
∥
x
∥
=
1
,
∥
y
∥
=
1
\|x\| = 1,\|y\| = 1
∥x∥=1,∥y∥=1,则此时两个向量之间的内积距离就是余弦距离 (Cosine Similarity):
Cosine Similarity
=
cos
θ
=
x
⋅
y
∥
x
∥
∥
y
∥
=
∑
i
=
1
n
x
i
y
i
∑
i
=
1
n
x
i
2
∑
i
=
1
n
y
i
2
\text{Cosine Similarity} = \cos \theta = \frac{\mathbf{x}\cdot\mathbf{y}}{\|\mathbf{x}\|\|\mathbf{y}\|}=\frac{\sum_{i=1}^{n}x_iy_i}{\sqrt{\sum_{i=1}^{n}x_i^2}\sqrt{\sum_{i=1}^{n}y_i^2}}
Cosine Similarity=cosθ=∥x∥∥y∥x⋅y=∑i=1nxi2∑i=1nyi2∑i=1nxiyi
3. 在 Sophon TPU 上的接口实现
若对底库进行暴力搜索,选出与实例最接近的
K
K
K 个向量,则意味着要一一计算检索向量与所有底库向量之间的距离值,然后对距离值排序得到最前面的
K
K
K 个距离值,该距离值的索引就是对应的底库向量的索引。针对全空间的搜索具有最高的召回率 (Recall),但检索速度和内存利用等差强人意。
因此,我们可以考虑两种提高检索速度的策略:一是减小向量 (采用减小维度、量化等方法);二是缩小检索的空间 (采用聚类、将向量调整成树结构等方法)。近似最近邻 (Approximate Nearest Neighbor, ANN) 方法实际将底库全空间分割成许多子空间,通过快速遍历这些子空间,大大缩减遍历的空间范围以提高检索速度。在 ANN 中,我们常采用矢量量化方法将一个向量空间中的点用其中的一个有限子集进行编码,其中的经典方法就是乘积量化 (Prduct Quantization, PQ)。
针对上述遍历底库进行
K
K
K 最近邻搜索的方式,Faiss 库提供了 indexflat 的接口;针对采用乘积量化方法来降低内存占用并提高检索速度的方式,Faiss 库提供了 indexPQ 的接口。
Faiss 库的 indexflat 包含有 L2 和 IP 两个距离测度,同时用 CUDA 编程利用 GPU 实现硬件加速。 indexPQ 包含有对称距离 (Symmetric distance computation, SDC) 和非对称距离 (Asymmetric distance computation, ADC) 两个距离测度,区别在于对称距离是将检索向量与底库向量之间的距离近似为二者对应量化后的编码之间的距离,而非对称距离仅将检索向量与量化后的底库向量编码之间的距离,相较之下非对称距离损失较小,更接近两个向量之间的真实距离。这两种间接近似求取的距离本质上仍旧采用 L2 和 IP 两个距离测度。
我们在 Sophon TPU (Tensor Processing Unit) 架构上实现了 Faiss 库的 indexflat 和 indexPQ 接口,发挥了 Sophon TPU 的最大性能。
3.1 Sophon TPU
新一代的 Sophon TPU 包含有
64
64
64 个 NPU (Neural Network Processing Unit),每一个 NPU 是一个独立的内存空间,有多个 EU (Execution Unit)。在同一时刻 NPU 可同时执行同样的计算指令对存储在不同的 NPU 中的不同的数据进行运算,是一个标准的 SIMD (Single Instruction Multiple Data) 结构。下图是 Sophon TPU 的架构图。
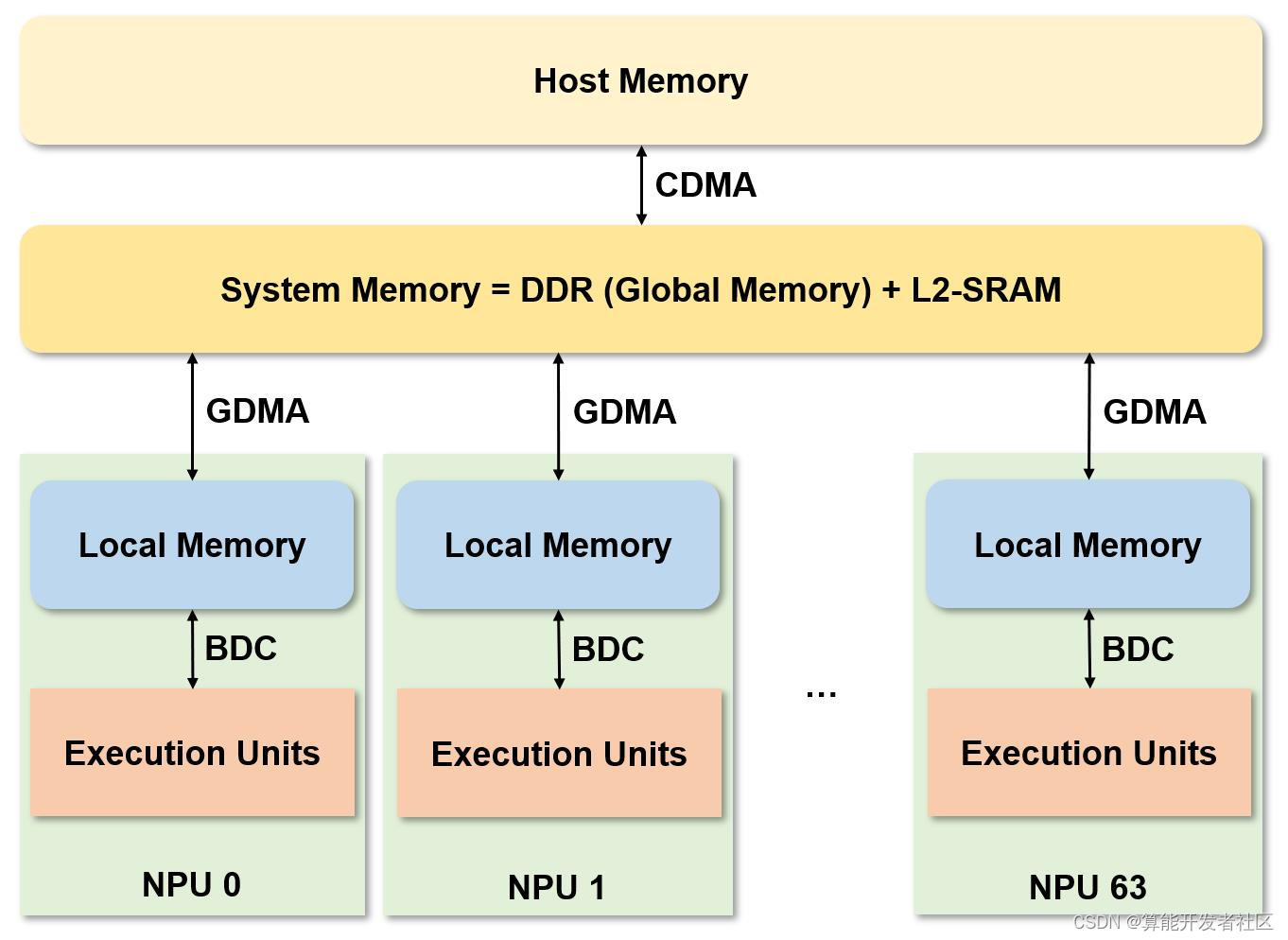
整个 TPU 加速计算过程,首先利用 CDMA 将数据从 host 端传入 TPU 的系统内存 (System Memory) 中,其中片上内存 L2-SRAM 作为缓存使用。随后,利用 GDMA 从 DDR (Global memory) 搬运到 NPU (Local memory),在 NPU 中利用 BDC 指令调用 EU 进行运算,然后将运算结果利用 GDMA 搬运回 DDR。
3.2 indexflat 实现
遍历式计算底库向量与多个检索向量的内积距离,实际是计算检索向量组成的左矩阵与底库向量所组成的右矩阵 (需要转置存储) 的乘积,这样得到的结果矩阵就是左矩阵的每一行和右矩阵的每一列的计算结果。将得到的内积距离矩阵的每一行都进行降序排序,每一行取前
K
K
K 个最大的内积距离值及其对应的索引值,这样就能得到最终的检索结果,输出底库中与检索向量最相似的前
K
K
K 个向量。
根据上述计算过程描述,我们可以将基于内积距离的全库检索过程转换成矩阵乘积计算和 batch topK 的实现。
需要注意的是,Faiss 库中是采用的 L2 距离的平方值进行测度,其实际的计算可根据下面的式子进行转换:
L
2
(
x
,
y
)
2
=
∑
i
=
1
n
∣
x
i
−
y
i
∣
2
=
∥
x
∥
2
+
∥
y
∥
2
−
2
x
y
L_2(\mathbf{x},\mathbf{y})^2=\sum_{i=1}^n|x_i-y_i|^2=\|\mathbf{x}\|^2+\|\mathbf{y}\|^2-2\mathbf{x}\mathbf{y}
L2(x,y)2=i=1∑n∣xi−yi∣2=∥x∥2+∥y∥2−2xy
可见,两个向量之间的 L2 距离的平方等于两个向量的内积距离的
−
2
-2
−2 倍再加上各自的 L2 范数的平方值。这样,基于 L2 距离的全库检索过程可转换成常数
−
2
-2
−2 乘上矩阵乘积、加上两个 bias 以及 batch topK 的实现。此外,在大多数应用场景中,底库的数据量很大,若每次检索都要 TPU 重新计算底库的 L2 范数的平方值,会对资源造成极大的浪费。因此,在 add 阶段可以利用 CPU 将向量的 L2 范数的平方值计算出来存放进底库;search 阶段,将底库和检索向量及其对应的 L2 范数的平方值从 DDR 搬运至 TPU 的 local memory 中进行计算。
200
W
200\text{W}
200W 的底库,向量维度为
256
256
256,数据类型为
FP
32
\text{FP}32
FP32,这样仅底库所需要的 DDR 存储空间就为
200
W
×
4
×
256
≈
2
GB
200\text{W} \times 4 \times 256 \approx 2 \text{GB}
200W×4×256≈2GB。为加速数据搬运和运算,我们采用数据切分的方式分批次搬运底库和检索向量分别组成的矩阵块,其次我们采用 GDMA 搬运和 BDC 计算并行的方式提高整体性能。最终测试我们所实现的 indexflatIP 和 indexflatL2 的 search 性能,在
200
W
200\text{W}
200W 底库,向量维度为
256
256
256,检索向量的个数分别为
1
1
1 和
64
64
64 的情况下在 Sophon TPU 上得到下表中的耗时 (单位:
ms
\text{ms}
ms) 数据。为了比对结果,我们同时在 TESLA T4 上测试了原始 Faiss 库对应的两个 search 接口的耗时。
| Sophon TPU | TESLA T4 | |||||
| vec_dims | topk | db_num | query_num | indexflatIP | indexflatL2 | search |
| 256 | 100 | 200W | 1 | 40 | 40 | 23 |
| 64 | 89 | 86 | 33 | |||
3.3 indexPQ 实现
针对 PQ,在 train 阶段,将底库中的每一个向量进行拆分,拆分后的每一个子空间经 K-means 聚类 (用 L2 距离的平方值进行测度) 后生成
256
=
2
8
256=2^8
256=28 个聚类中心,得到一个码表,保证了用
8
8
8 比特即一个字节表示每一个码本中的量化编码。这样底库中每一个向量切分后的子段都能用所在子空间的聚类中心来近似表示,这样仅用很短的编码就可以表示一个底库向量,实现量化的目的,从而减少内存空间的占用。
在 search 阶段,以非对称距离为例,将检索向量拆分成相同数量的子段,在对应的每一个子空间中,计算检索向量子段到该子空间聚类中心的距离得到距离表。依据码表中的编码查询距离表,将所有子段对应的距离取出并求和,得到底库中的向量到查询向量间的非对称距离。最后将非对称距离进行排序得到想要的前
K
K
K 个与检索向量最相似的底库向量的索引值。
在 Sophon TPU 上实现 PQ 的 search 阶段,对于非对称距离,过程为计算距离表、查找距离表以及 topK 的过程;对于对称距离,过程为查询对称距离码表得到距离表、查询距离表以及 topK 的过程。
我们测试了将
256
256
256 维的向量切分成
32
32
32 个子段,在
200
W
200\text{W}
200W 和
2000
W
2000\text{W}
2000W 底库上检索
1
1
1 个向量的耗时 (单位:
ms
\text{ms}
ms)。经量化之后,对于
FP
32
\text{FP}32
FP32 的
200
W
200\text{W}
200W 底库,在 DDR 上存储对应的量化码表仅占用
32
×
256
×
8
×
4
=
256
KB
32\times 256\times 8\times 4 = 256\text{KB}
32×256×8×4=256KB,极大降低了所需的内存空间。与 indexflat 相比,针对
200
W
200\text{W}
200W 的底库检索
1
1
1 个向量的时间从
40
ms
40\text{ms}
40ms 降至约
4
ms
4\text{ms}
4ms,检索耗时缩短了
10
10
10 倍。
我们同时在 TESLA T4 上测试了原始 Faiss 库 indexPQ 的 search 接口非对称距离的耗时,TPU 上
200
W
200\text{W}
200W 底库 top100 耗时不到
4
ms
4\text{ms}
4ms,TESLA T4 上大约是
12
ms
12\text{ms}
12ms;
2000
W
2000\text{W}
2000W 底库 top100 耗时大约是
34
ms
34\text{ms}
34ms,TESLA T4 上是
112
ms
112\text{ms}
112ms,由此可见,在 Sophon TPU 上实现的 indexPQ 的单向量查询的性能优于 TESLA T4。
| m | dim | ksub | datatype | codetype |
| 32 | 256 | 256 | FP32 | INT8 |
| metric | database | topk | ADC | SDC |
| L2 | 200W | 100 | 3.682 | 3.422 |
| 1000 | 9.643 | 9.656 | ||
| 2000W | 100 | 32.27 | 30.053 | |
| 1000 | 101.928 | 99.757 | ||
| IP | 200W | 100 | 3.695 | 3.422 |
| 1000 | 9.541 | 9.656 | ||
| 2000W | 100 | 32.23 | 30.053 | |
| 1000 | 102.018 | 99.757 |







![[附源码]JAVA毕业设计社区图书馆借阅管理系统(系统+LW)](https://img-blog.csdnimg.cn/ac802e000bd34a14a5e2519ea028877e.png)