【C语言督学训练营 第十四天】二叉树真题实战 ----- 层序建树、前中后序遍历、求树的WPL

news2024/11/15 5:49:32

文章目录

  • 前言
  • 树概念
  • 二叉树
  • 层序建树
  • 四种遍历二叉树的方式
    • 层次遍历
    • 前序遍历
    • 中序遍历
    • 后续遍历
  • 真题实战！

前言

今天进行总结的是考研408有关二叉树的基础知识，是王道C语言督学营的第十四天，随着课程的深入，代码实战的难度慢慢的上来了，如果觉着代码实战有困难，那么我推荐先在纸上画一画，然后再上代码，今天这节课主要进行了二叉树的层序建树，二叉树的前中后序遍历，以及层序遍历，最后针对一道2014年的考研真题进行了解析！
先预热一下：
在这里插入图片描述
在这里插入图片描述

树概念

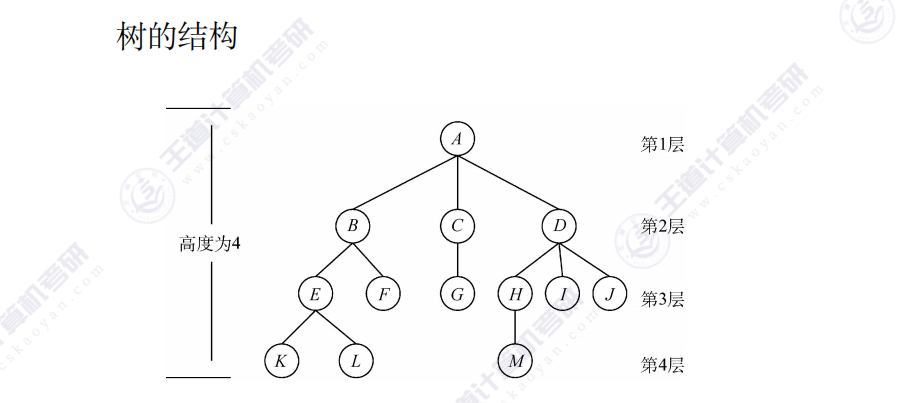
树是n (n≥0）个节点的有限集。当n = O时，称为空树。
在任意一棵非空树中应满足:

  • 1)有且仅有一个特定的称为根的结点。
  • 2)当n >1时，其余节点可分为m (m > 0）个互不相交的有限集T1，T2,…", Tm，其中每个集合本身又是一棵树，并且称为根的子树。

树作为一种逻辑结构，同时也是一种分层结构，具有以下两个特点:

  • 1）树的根结点没有前驱，除根结点外的所有结点有且只有一个前驱。
  • 2）树中所有结点可以有零个或多个后继。
    在这里插入图片描述

二叉树

二叉树是一种特殊的树形结构，其特点是每个结点至多只有两棵子树(即二叉树中不存在度大于2的结点)，并且二叉树的子树有左右之分,其次序不能任意颠倒。
与树相似，二叉树也以递归的形式定义。二叉树是n (n≥O)个结点的有限集合:

  • ①或者为空二叉树，即n= 0.
  • ②或者由一个根结点和两个互不相交的被称为根的左子树和右子树组成。左子树和右子树又分别是一棵二叉树。

二叉树又可分为满二叉树与完全二叉树，两者形如下图：
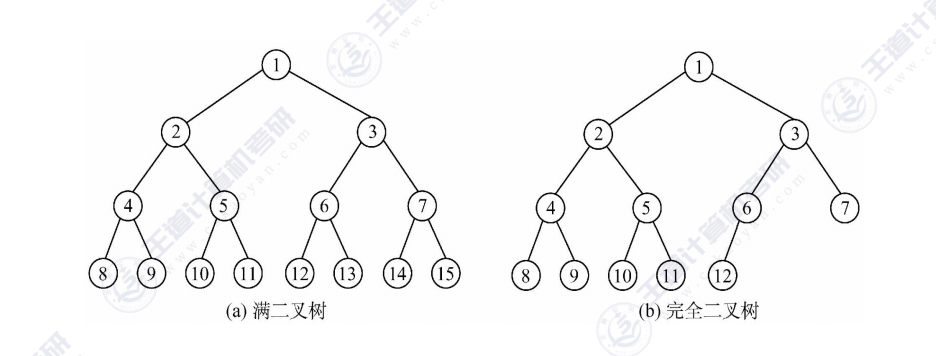
在这里插入图片描述
满二叉树与完全二叉树，因为其独有的特性，采用顺序存储结构存储极为方便。后面排序时会进行实战！
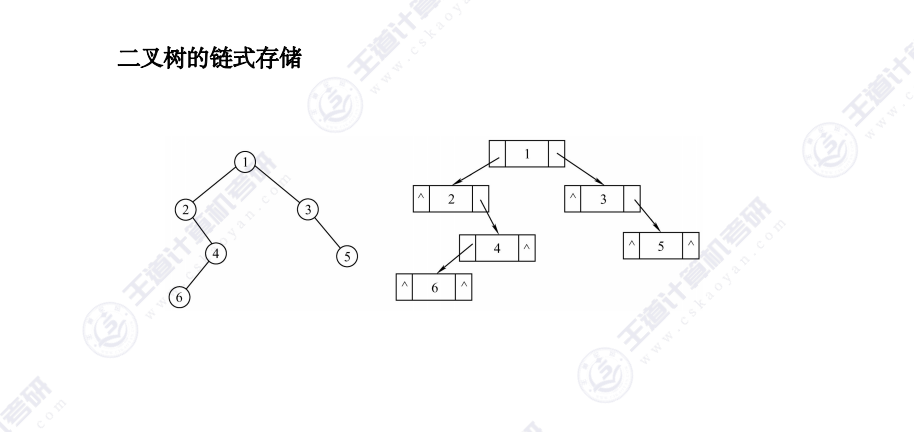
在这里插入图片描述
在这里插入图片描述
链式二叉树节点结构定义如下：
在这里插入图片描述
这里仅仅是对二叉树进行了简要的介绍，真正的知识要比这个多得多，后面在介绍数据结构的时候会详细介绍！记住下面图片的内容，然后开启我们今天的实战！
在这里插入图片描述

层序建树

层析建树我们需要借助一个辅助队列进行实现，我的思路是，使用队列记录数节点的输入顺序，然后根据节点的左子树右子树指针是否为空向其子树填值，当左子树右子树均有值的时候就向下一个节点填充，每次填充的内容是新入队的节点！直到将辅助队列遍历一遍，二叉树也就层序建树成功！
建树代码如下：
节点的定义：

//
// Created by 123 on 2023/2/20.
//

#ifndef MYTEST_BITSTRUCT_H
#define MYTEST_BITSTRUCT_H
//基础元素类型
#define  ElementData int
#define ElementDataEnd -1
//二叉树的节点
struct BiTNode{
    ElementData data;
    struct BiTNode *leftNode;
    struct BiTNode *rightNode;
};
typedef struct BiTNode BiTNode;
//辅助队列（通过这个队列层次建树）
struct auxiliary{
    // 指向二叉树中的节点
    struct BiTNode* p;
    struct auxiliary *next;
};
typedef struct auxiliary tagQueue;
#endif //MYTEST_BITSTRUCT_H

代码中的前两个函数是为了初始化节点方便设计的；

BiTNode* newNode(ElementData e){
    BiTNode *pnew=(BiTNode*) malloc(sizeof (BiTNode));
    pnew->leftNode=NULL;
    pnew->rightNode=NULL;
    pnew->data=e;
    return pnew;
}
tagQueue* newTagNode(BiTNode* pnew){
    tagQueue *p=(tagQueue *) malloc(sizeof (tagQueue));
    p->next=NULL;
    p->p=pnew;
    return p;
}
BiTNode *Sequence_tree_building(){
    BiTNode *tree=NULL,*pnew=NULL;
    tagQueue *tail=NULL,*tagQ=NULL,*p;
    ElementData e;
    while(scanf("%d",&e)){
        if(e==ElementDataEnd){
            break;
        }
        //将信息写入新生成的节点
        pnew=newNode(e);
        p=newTagNode(pnew);
        // 写成NULL==tail是为了防止tail=NULL的情况发生;
        //改变指针之间的关系，将节点插入相应位置
        if(NULL==tree){
            //此分支创建二叉树，创建辅助队列
            tree=pnew;
            tail=p;
            tagQ=tail;
            continue;
        }else{
            //将新节点添加到队尾
            tail->next=p;
            tail=tail->next;
        }
        // 精妙之处，通过辅助队列构建二叉树
        if(tagQ->p->leftNode==NULL){
            tagQ->p->leftNode=pnew;
        }else if(tagQ->p->rightNode==NULL){
            // 此分支多一句是因为,这种建树方式是层序建树（这颗子树左右都有的话会向兄弟树根偏移，而辅助队列下一个就是本层的兄弟树根）
            tagQ->p->rightNode=pnew;
            tagQ=tagQ->next;
        }
    }
    return tree;
}

建树结果，可以看到树中每一层节点对应的data;
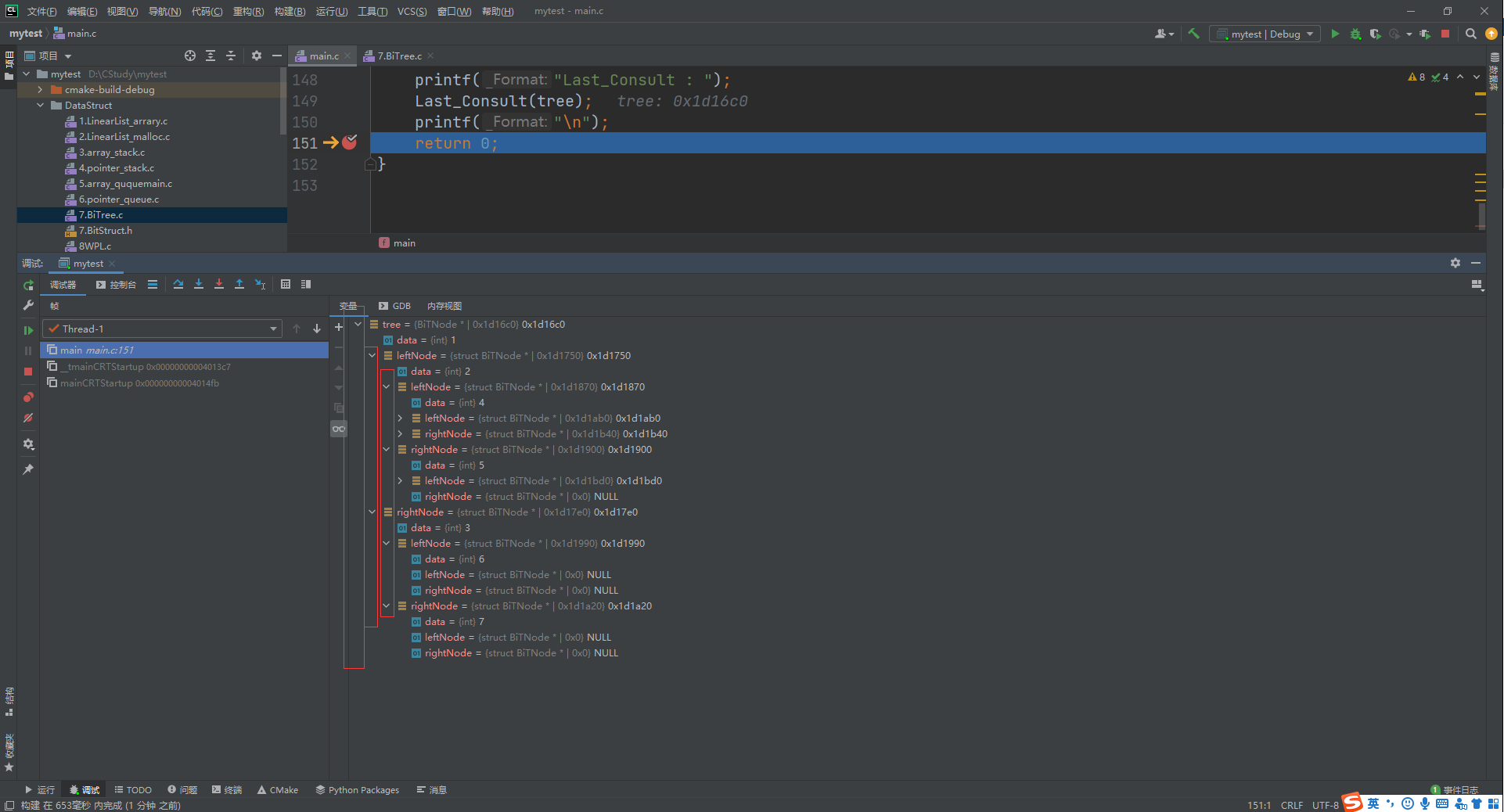
在这里插入图片描述

四种遍历二叉树的方式

遍历就是将树中的所有节点访问一遍。

层次遍历

借助辅助队列，其实树的层次遍历就是一次BFS的过程，其英文全称是Breadth First Search。又称广度优先搜索，宽度优先搜索。实现过程如下：

// ---------------层序遍历----------------BFS//
//这种实现思路使用的是一级指针，还可以通过二级指针实现//
//直接判断节点的两个子节点是否为空，不为空添加到队列//
void Layer_Consult(BiTNode* tree){
    tagQueue *head=(tagQueue*) malloc(sizeof (tagQueue)),*tail,*q;
    head->p=tree;
    head->next=NULL;
    tail=head;
    while (head!=NULL){
        printf("%d ",head->p->data);
        //入队
        if(head->p->leftNode!=NULL){
            tagQueue *p=(tagQueue*) malloc(sizeof (tagQueue));
            p->p=head->p->leftNode;
            p->next=NULL;
            tail->next=p;
            tail=p;
        }
        if(head->p->rightNode!=NULL){
            tagQueue *p=(tagQueue*) malloc(sizeof (tagQueue));
            p->p=head->p->rightNode;
            p->next=NULL;
            tail->next=p;
            tail=p;
        }
        q=head;
        head=head->next;
        free(q);
        q=NULL;
    }
}

以下三种遍历方式较为简单，就不给出思路解释了，实现方式均是递归（因为树本质就是递归实现，估计考研不会限制大家使用递归还是非递归方法遍历，递归常常可以将有关树的问题简化的非常简单）。

前序遍历

// ---------------先序遍历----------------//
void Pre_Consult(BiTNode* tree){
    if(tree==NULL){
        return;
    }
    printf("%d ",tree->data);
    Pre_Consult(tree->leftNode);
    Pre_Consult(tree->rightNode);
}

中序遍历

// ---------------中序遍历----------------//
void Middle_Consult(BiTNode* tree){
    if(tree==NULL){
        return;
    }
    Middle_Consult(tree->leftNode);
    printf("%d ",tree->data);
    Middle_Consult(tree->rightNode);
}

后续遍历

// ---------------后序遍历----------------//
void Last_Consult(BiTNode* tree){
    if(tree==NULL){
        return;
    }
    Last_Consult(tree->leftNode);
    Last_Consult(tree->rightNode);
    printf("%d ",tree->data);
}

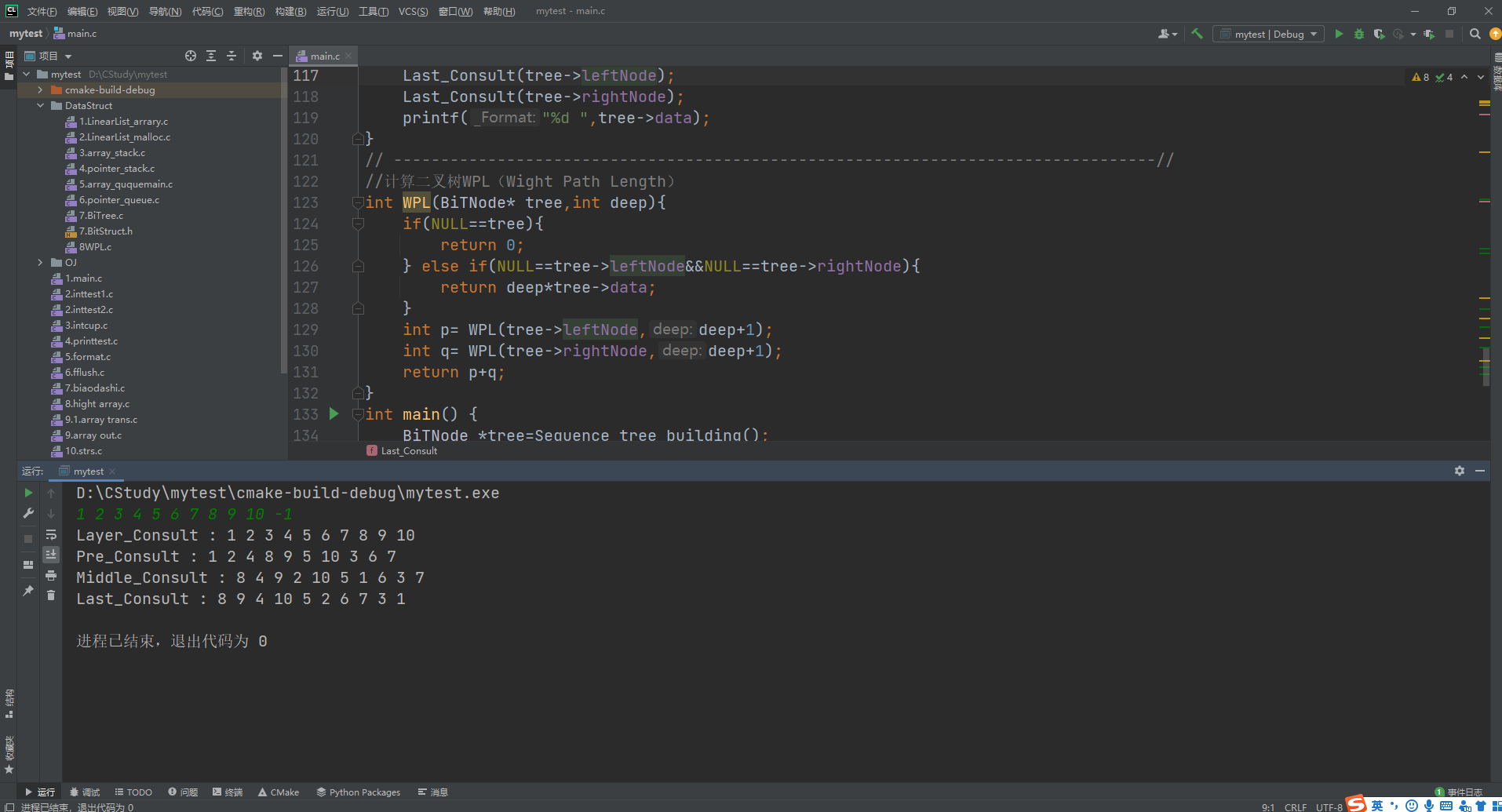
以下图片为层序、前、中、后序遍历实战结果：
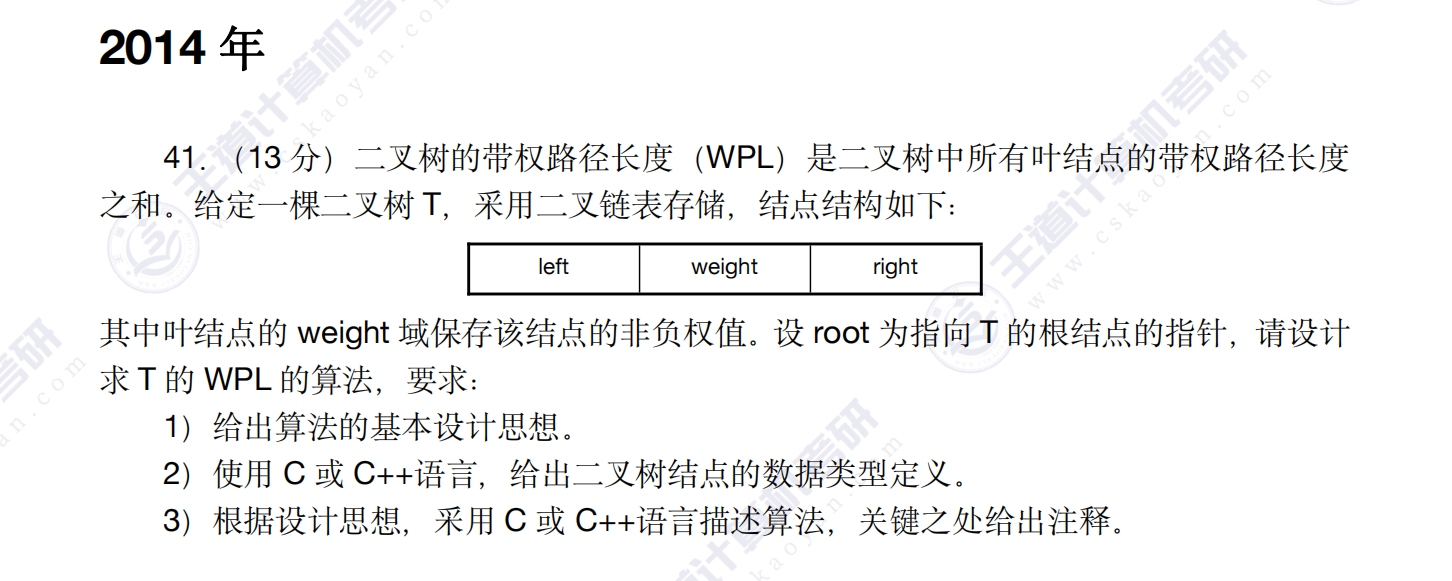
在这里插入图片描述

真题实战！

在这里插入图片描述
又到了真题实战环节，今天这个实战很简单，本质是探索叶子节点及树的深度（也就是遍历一遍即可）WPL只树的带权路径长度，也就是叶子节点权值*其深度，然后相加之和。

（1）使用递归算法，参数负责接受树根与深度，当树中节点左子树右子树均为空时返回其深度与权值的乘积，当传入的节点为空时返回0，然后用两个变量依次接收左子树右子树的返回值，函数最后将左子树右子树返回值相加再返回，函数递归完毕最终的返回值就是我们所求得总的WPL。
（2）给出二叉树节点数据类型定义：

struct BiTNode{
    ElementData data;
    struct BiTNode *leftNode;
    struct BiTNode *rightNode;
};

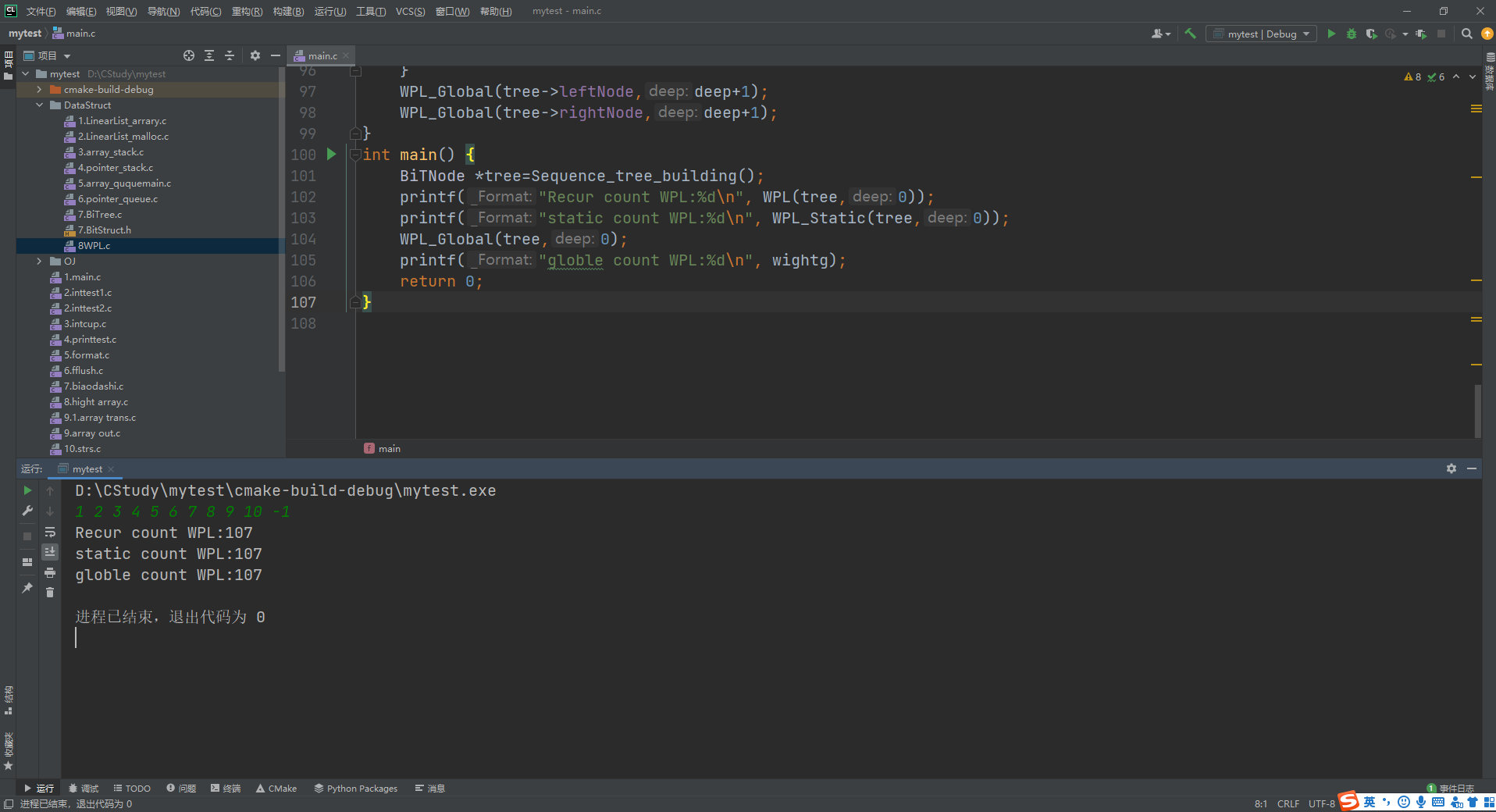
（3）代码实现，这里给出了三种方法，其中第一种是算法描述部分的方法，第二种是使用static变量，第三种是使用全局变量。三种方式实现结果如下：
在这里插入图片描述

//
// Created by Zhu Shichong on 2023/1/9.
//
#include <stdio.h>
#include <stdlib.h>
#include "BitStruct.h"
#define bool int
#define true 1
#define false 0
//封装函数初始化一个根节点
BiTNode* newNode(ElementData e){
    BiTNode *pnew=(BiTNode*) malloc(sizeof (BiTNode));
    pnew->leftNode=NULL;
    pnew->rightNode=NULL;
    pnew->data=e;
    return pnew;
}
tagQueue* newTagNode(BiTNode* pnew){
    tagQueue *p=(tagQueue *) malloc(sizeof (tagQueue));
    p->next=NULL;
    p->p=pnew;
    return p;
}

// -------------------层序建树------------------------------//
BiTNode *Sequence_tree_building(){
    BiTNode *tree=NULL,*pnew=NULL;
    tagQueue *tail=NULL,*tagQ=NULL,*p;
    ElementData e;
    while(scanf("%d",&e)){
        if(e==ElementDataEnd){
            break;
        }
        //将信息写入新生成的节点
        pnew=newNode(e);
        p=newTagNode(pnew);
        // 写成NULL==tail是为了防止tail=NULL的情况发生;
        //改变指针之间的关系，将节点插入相应位置
        if(NULL==tree){
            //此分支创建二叉树，创建辅助队列
            tree=pnew;
            tail=p;
            tagQ=tail;
            continue;
        }else{
            //将新节点添加到队尾
            tail->next=p;
            tail=tail->next;
        }
        // 精妙之处，通过辅助队列构建二叉树
        if(tagQ->p->leftNode==NULL){
            tagQ->p->leftNode=pnew;
        }else if(tagQ->p->rightNode==NULL){
            // 此分支多一句是因为,这种建树方式是层序建树（这颗子树左右都有的话会向兄弟树根偏移，而辅助队列下一个就是本层的兄弟树根）
            tagQ->p->rightNode=pnew;
            tagQ=tagQ->next;
        }
    }
    return tree;
}

//计算二叉树WPL（Wight Path Length）递归方式实现
int WPL(BiTNode* tree,int deep){
    if(NULL==tree){
        return 0;
    } else if(NULL==tree->leftNode&&NULL==tree->rightNode){
        return deep*tree->data;
    }
    int p= WPL(tree->leftNode,deep+1);
    int q= WPL(tree->rightNode,deep+1);
    return p+q;
}
//计算二叉树WPL（Wight Path Length）静态变量方式实现
//这种方式纯属遍历一遍二叉树！
int WPL_Static(BiTNode* tree,int deep){
    static wight=0;
    if(NULL==tree){
        return 0;
    }
    if(NULL==tree->leftNode&&NULL==tree->rightNode){
        wight+=deep*tree->data;
    }
    WPL_Static(tree->leftNode,deep+1);
    WPL_Static(tree->rightNode,deep+1);
    return wight;
}
//计算二叉树WPL（Wight Path Length）全局变量方式实现
//这种方式纯属遍历一遍二叉树！
int wightg=0;
void WPL_Global(BiTNode* tree,int deep){
    if(NULL==tree){
        return ;
    }
    if(NULL==tree->leftNode&&NULL==tree->rightNode){
        wightg+=deep*tree->data;
    }
    WPL_Global(tree->leftNode,deep+1);
    WPL_Global(tree->rightNode,deep+1);
}
int main() {
    BiTNode *tree=Sequence_tree_building();
    printf("Recur count WPL:%d\n", WPL(tree,0));
    printf("static count WPL:%d\n", WPL_Static(tree,0));
    WPL_Global(tree,0);
    printf("globle count WPL:%d\n", wightg);
    return 0;
}

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/684325.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

MyCat01——如何实现MySQL中的主从复制

MyCat01——如何实现MySQL中的主从复制

1 问题 数据对于我们来说是一项最重要的资产&#xff0c;因为数据丢失带来的损失&#xff0c;对于一家公司来说&#xff0c;有时也是毁灭性的。 那么如何确保数据安全&#xff0c;不因断电或系统故障带来数据丢失呢&#xff1f; 当用户增加&#xff0c;对数据库的访问量也随…
阅读更多...
推荐一款好用的时序预测工具——Alibaba DChain Forecast

推荐一款好用的时序预测工具——Alibaba DChain Forecast

前言 绝大部分行业场景&#xff0c;尤其是互联网、量化行业&#xff0c;每天都会产生大量的数据。金融领域股票价格随时间的走势&#xff1b;电商行业每日的销售额&#xff1b;旅游行业随着节假日周期变化的机票酒店价格等。我们称这种不同时间收到的&#xff0c;描述一个或多…
阅读更多...
Ajax技术的秘密揭秘：异步传输，高效交互

Ajax技术的秘密揭秘：异步传输，高效交互

文章目录 I. 什么是AjaxAjax的定义和起源Ajax与传统的Web应用程序之间的区别 II. Ajax的工作原理Ajax的基本原理Ajax如何通过异步传输实现无需刷新页面 III. Ajax的应用场景在Web应用程序中应用Ajax的优势Ajax在哪些场景中使用 IV. Ajax的组成部分和APIXHR对象FormData对象Fetc…
阅读更多...
用postman进行web端自动化测试

用postman进行web端自动化测试

目录 前言 一、抓包&#xff08;使用Charles抓包工具&#xff09; 二、选择请求方法 三、填写url地址 四、填写Header 五、填写body 六、断言&#xff08;Tests页&#xff09; 七、获取动态参数——例如token 八、设置静态参数&#xff08;请求地址、账号密码等&#x…
阅读更多...
【Django-功能优化】存储、循环、操作选择对代码性能的影响

【Django-功能优化】存储、循环、操作选择对代码性能的影响

功能开发背景 港口货轮需要进行集装箱的装卸任务&#xff1a; 船上的每一个集装箱&#xff0c;可以用三个维度的坐标来唯一定位&#xff1a;(bay, column, layer)&#xff0c;这三个维度结合其他一些固有信息&#xff0c;构成了一个箱子的字段属性&#xff0c;存储在箱子数据表…
阅读更多...
百度的人脸识别的技术

百度的人脸识别的技术

百度的人脸识别的技术 1.基本概念 分组&#xff1a;分组ID&#xff08;group_id&#xff09;&#xff1a;分组ID用于对一组相关的人脸进行分组和管理。你可以根据自己的需求&#xff0c;将不同的人脸数据分配到不同的分组中。例如&#xff0c; 你可以根据人员的职位、部门或其…
阅读更多...
Nginx优化安全防盗链

Nginx优化安全防盗链

1.Nginx的页面优化 1.1 Nginx的网页压缩 在Nginx的ngx_http_gzip_module压缩模块提供对文件内容压缩的功能。进行相关的配置修改&#xff0c;就能实现Nginx页面的压缩&#xff0c;达到节约带宽&#xff0c;提升用户访问速度 1.2 配置Nginx的图片缓存 当Nginx将网页数据返回给…
阅读更多...
阿里云企业邮箱免费版、标准版、集团版和尊享版区别

阿里云企业邮箱免费版、标准版、集团版和尊享版区别

阿里云企业邮箱版本分为免费版、标准版、集团版和尊享版&#xff0c;除了价格区别&#xff0c;功能方面有什么差异&#xff1f;如何选择企业邮箱版本&#xff1f;免费版0元适合初创型企业&#xff0c;标准版适合大、中、小型企业使用&#xff0c;涉及子公司之间邮箱通讯可以选择…
阅读更多...
jQuery学习

jQuery学习

原生实现计数器 <!DOCTYPE html> <html lang"en"> <head><meta charset"UTF-8"><meta http-equiv"X-UA-Compatible" content"IEedge"><meta name"viewport" content"widthdevice-wi…
阅读更多...
getopt_long 函数的使用

getopt_long 函数的使用

getopt_long 函数的使用网上已经有很多了&#xff0c;这里只是记录一下方便自己后续查找。首先函数原型声明&#xff1a; #include <getopt.h>int getopt_long(int argc, char *argv[],const char *optstring,const struct option *longopts, int *longindex); 函数是用…
阅读更多...
Navicat使用导入向导批量插入数据到数据库

Navicat使用导入向导批量插入数据到数据库

Mybatis,"可持久层数据库框架" Html,"超文本标记语言" Css,"网页外设计语言" JavaScript,"用户行为交互" Jquery,"提升网页开发效率的一种框架" Vue,"前端开发框架" Vant,"前开发预装组件库" git,"…
阅读更多...
SM2算法对比RSA算法，有哪些优势？

SM2算法对比RSA算法，有哪些优势？

SM2算法和RSA算法都是公钥密码算法&#xff0c;SM2算法是一种更先进安全的算法&#xff0c;在安全性能、速度性能等方面都优于RSA算法&#xff0c;在我国商用密码体系中被用来替换RSA算法。国家密码管理局于2010年12月17日发布了SM2算法&#xff0c;并要求现有的基于RSA算法的电…
阅读更多...
《面试1v1》Redis基础

《面试1v1》Redis基础

&#x1f345; 作者简介&#xff1a;王哥&#xff0c;CSDN2022博客总榜Top100&#x1f3c6;、博客专家&#x1f4aa; &#x1f345; 技术交流&#xff1a;定期更新Java硬核干货&#xff0c;不定期送书活动 &#x1f345; 王哥多年工作总结&#xff1a;Java学习路线总结&#xf…
阅读更多...
Golang/Python 调用 openAI 的API 详解

Golang/Python 调用 openAI 的API 详解

学习目标&#xff1a; OpenAI API介绍 学习如何通过 Golang 使用 OpenAI 的 API OpenAI 的常用的参数及其说明 了解OpenAI API 中令牌&#xff08;tokens) OpenAI API 提供了几个不同的终端点&#xff08;endpoints&#xff09;和模式&#xff08;modes&#xff09; 复杂和…
阅读更多...
【已解决】Java 中导入excel时使用 trim() 无法去除空格的解决方法

【已解决】Java 中导入excel时使用 trim() 无法去除空格的解决方法

使用trim无法去除空格的解决方法 一、问题描述二、原因分析三、解决方案方案一&#xff1a;使用正则表达式方案二&#xff1a;使用String.strip()方案三&#xff1a;使用 hutool的 StrUtil.trim()方法 四、总结 一、问题描述 在excel导入操作时&#xff0c;读取cell中的字符串…
阅读更多...
自学Python 69 Selenium八大元素定位方法(新版BY方法)

自学Python 69 Selenium八大元素定位方法(新版BY方法)

Python Selenium八大元素定位方法(新版BY方法) 文章目录 Python Selenium八大元素定位方法(新版BY方法)前言一、常用的八种定位方法&#xff08;新旧对比&#xff09;二、查看网页元素三、八大元素定位示例1、id定位2、name定位3、class定位4、tag定位5、link定位6、partial_li…
阅读更多...
MySQL - 第9节 - MySQL内外连接

MySQL - 第9节 - MySQL内外连接

目录 1.内连接 2.外连接 2.1.左外连接 2.2.右外连接 3.简单案例 1.内连接 • 表的连接分为内连接和外连接。 • 内连接实际上就是利用where 子句对两种表形成的笛卡儿积进行筛选&#xff0c;我们前面学习的查询都是内连接&#xff0c;也是在开发过程中使用的最多的连接查…
阅读更多...
【C++】模板初级内容（函数模板，类模板）

【C++】模板初级内容（函数模板，类模板）

文章目录 前言一、函数模板1.1 函数模板概念1.2函数模板格式1.3模板的原理&#xff1a;1.4函数模板的实例化 二、类模板2.1 类模板的定义格式2.2定义与声明分离要注意的点 前言 告诉编译器一个模子&#xff0c;让编译器根据不同的类型利用该模子来生成代码 模板分为函数模板与类…
阅读更多...
MES系统常用的数据采集网关

MES系统常用的数据采集网关

随着制造业的数字化转型&#xff0c;MES&#xff08;制造执行系统&#xff09;在生产过程中的重要性日益凸显。MES系统作为连接企业资源和生产现场的桥梁&#xff0c;需要实时、准确地采集和整合工业设备的数据&#xff0c;以支持生产调度、质量管理、库存控制等关键业务。为了…
阅读更多...
探索Gradio Audio模块的change、clear和play方法

探索Gradio Audio模块的change、clear和play方法

❤️觉得内容不错的话&#xff0c;欢迎点赞收藏加关注&#x1f60a;&#x1f60a;&#x1f60a;&#xff0c;后续会继续输入更多优质内容❤️ &#x1f449;有问题欢迎大家加关注私戳或者评论&#xff08;包括但不限于NLP算法相关&#xff0c;linux学习相关&#xff0c;读研读博…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023