原视频为左程云的B站教学
文章目录
- 1 异或换值
- 2 求出数组中唯一一个出现奇数次的数
- 3 求出数组中的两个出现奇数次的数
异或:
10010
^ 01100
--------
11110
性质
- 0 ^ N = N,N ^ N = 0
- a ^ b = b ^ a (交换律)
- a ^ b ^ c = a ^ (b ^ c)(结合律) 同一堆数,不管异或计算顺序如何变化,异或一定是相同结果
1 异或换值
交换两个变量的值(而不引入额外临时空间)。注意 a 和 b 可以是不同变量想通数字,但是不可以是同一个变量。
a = a ^ b //第一行:a = a ^ b; b = b
b = a ^ b //第二行:a = a ^ b; b = b ^ a ^ b = a (因为b ^ b = 0, 0 ^ a = a)
a = a ^ b //第三行:a = a ^ b ^ a = b b = a
2 求出数组中唯一一个出现奇数次的数
要求时间复杂度O(n) 空间复杂度O(1)
void printOddTimesNum(const std::vector<int>& arr)
{
int eor = 0;
for (int cur : arr){
eor ^= cur;
}
cout << eor << endl;
}
// eor = 1 ^ 1 ^ 2 ^ 2 ^ 3 ^ 3 ^ .... ^ odd ^ 24 ^ 24 ^.....
// 最后 eor 会等于那个出现奇数次的,出现偶数次的数都被自己消除掉了
3 求出数组中的两个出现奇数次的数
数组有两个数字出现了奇数次,其他的数都是偶数
(要求时间复杂度O(n) 空间复杂度O(1))
- 我们还是一个奇数次的做法先得到 eor(全称exclusive OR),但最终eor会等于 a ^ b,因为偶数次的都变为0
- 因为这两个数不一样,所以如果把他们转换成二进制,至少有一个位是不同的(一个0,一个1)。eor在这个位上的异或计算结果必然是 0 ^ 1 = 1。 至少有一个: 巧妙,虽然也可能有很多个为1的位,但是我们只需要取出其中一个,这里为了方便,直接取eor上最右边一个为1的(利用 eor & (~eor + 1))。
- 取出eor最右边一个1是用来把数组元素分成两拨(该位为0的数,以及该位为1的数)。因为eor = a ^ b,且eor该位为1,因此a b在该位上必然不同,因此a b必然分别位于两拨数之中 (主要目的就是分开他俩)
- 然后关键操作来了:用新的eor’异或所有该位为1的数组元素。这一步同问题1.2,结果必然是a或者b,我们假设是eor’ = a。最后用eor’ ^ eor,则得到另一个奇数即eor = eor’ ^ eor = a ^ a ^ b = b。
#include <iostream>
#include <vector>
void printOddTimesNum2(const std::vector<int>& arr)
{
int eor = 0;
for (const int& cur : arr){
eor ^= cur;
}
// 目前 eor = a ^ b , eor != 0 且必然至少有一个位是1
int rightOne = eor & (~eor + 1);
int eor1 = 0;
for (const int& cur : arr){
if ((rightOne & cur) == rightOne){ // 与该位为1的组所有元素进行异或
eor1 ^= cur;
}
}
// eor1 得到的是a 或 b 不确定
cout << eor1 << ' ' << eor1 ^ eor << endl;
}
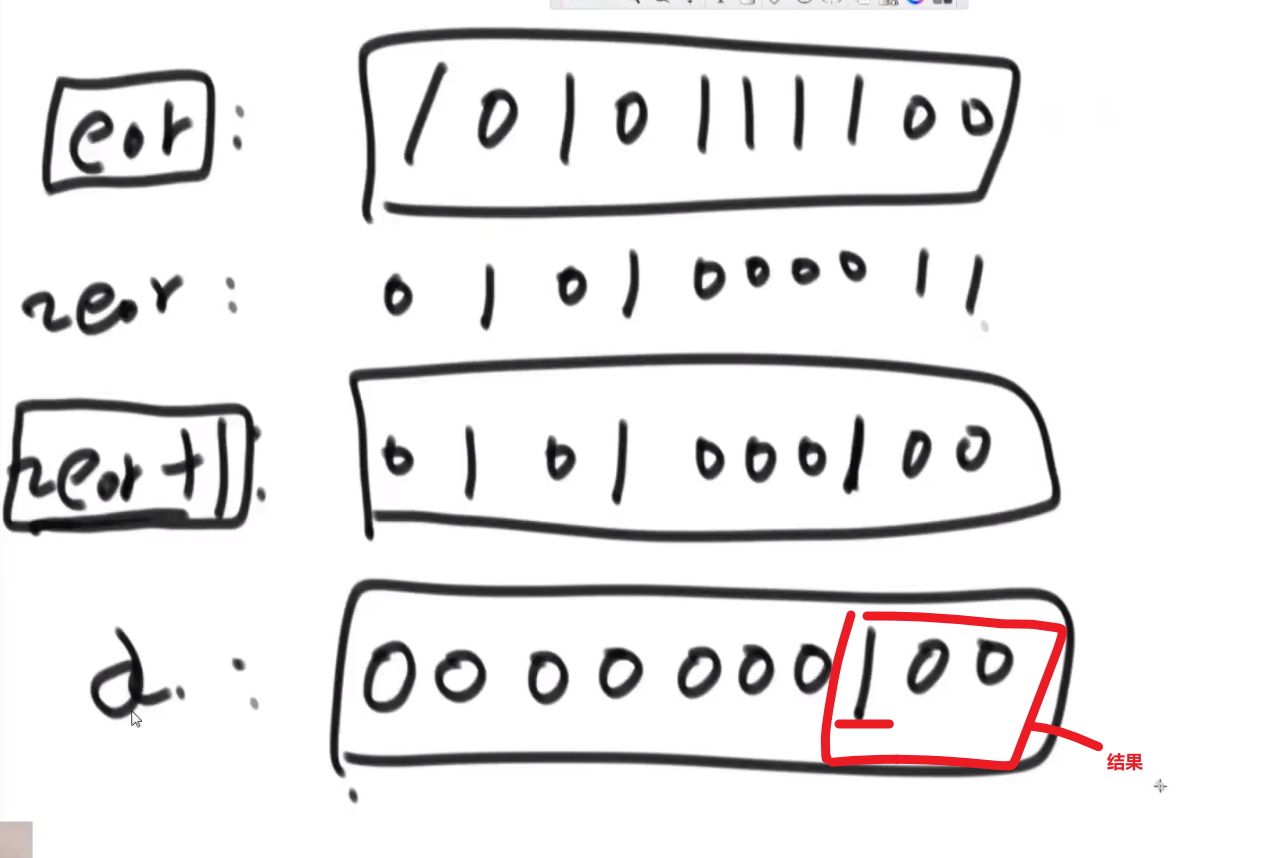
代码中 eor & (~eor + 1)的作用是,拿到目标二进制串的最末尾的1及其后边所有的0
假设eor为1010111100
我们可以使用eor & (~eor + 1)这个能提取出这个数 (eor) 的二进制最右边的 1 及其往后的值,即100