一、虚拟头节点

🌼 为了让代码更加精简，统一所有节点的处理逻辑，可以在最前面增加一个虚拟的头节点（不存储数据）

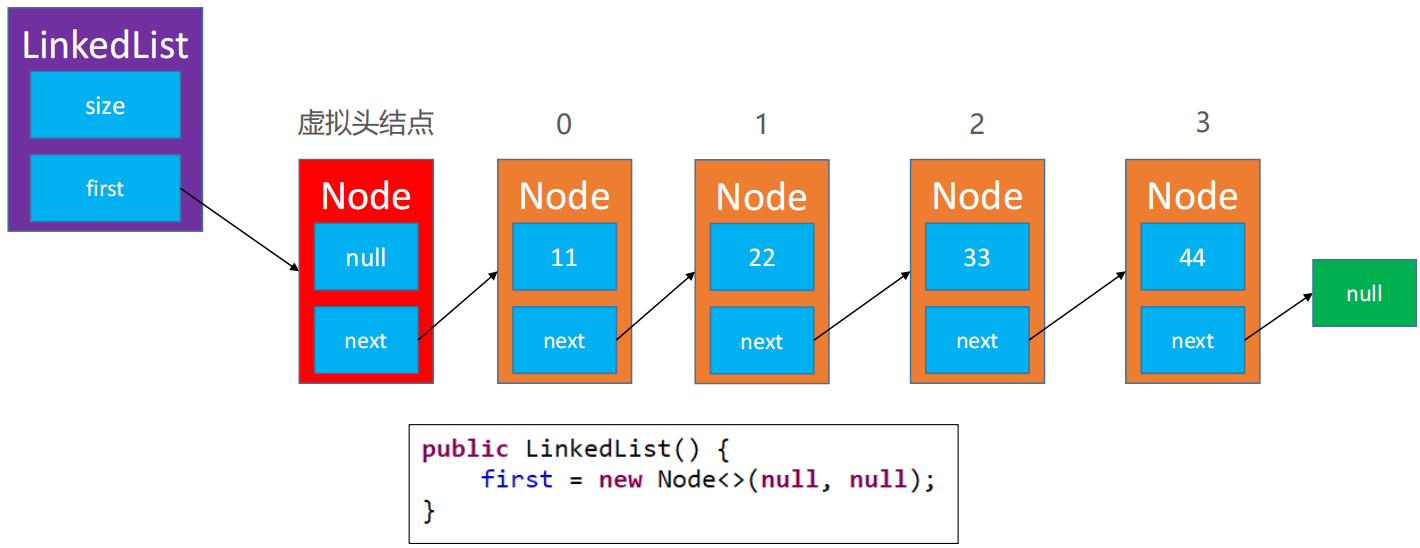
在这里插入图片描述
修改 node(int) 方法：

    /**
     * 返回 index 位置的节点
     */
    private Node<E> node(int index) {
        rangeCheck(index);

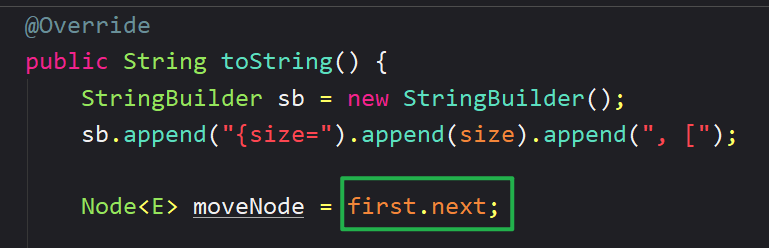
        // 从虚拟头节点的下一个节点开始寻找
        Node<E> moveNode = first.next;

        for (int i = 0; i < index; i++) {
            moveNode = moveNode.next;
        }

        return moveNode;
    }

修改添加和删除方法：

    @Override
    public void add(int index, E element) {
        rangeCheck4Add(index);

        // 拿到【index - 1】位置的节点
        Node<E> prev = (index == 0) ? first : node(index - 1);

        prev.next = new Node<>(element, prev.next);

        size++;
    }

    @Override
    public E remove(int index) {
        rangeCheck(index);

        Node<E> prev = (index == 0) ? first : node(index - 1);
        Node<E> node = prev.next;

        prev.next = node.next;

        size--;

        return node.element;
    }

在这里插入图片描述

二、数组的随机访问

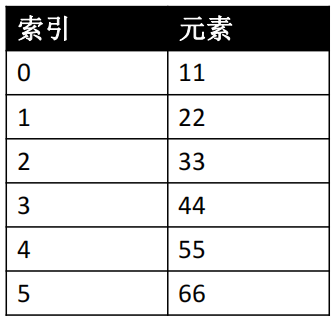
在这里插入图片描述
🎉数组的随机访问速度非常快
🎉elements[n] 的效率与 n 是多少无关

三、动态数组、链表复杂度分析

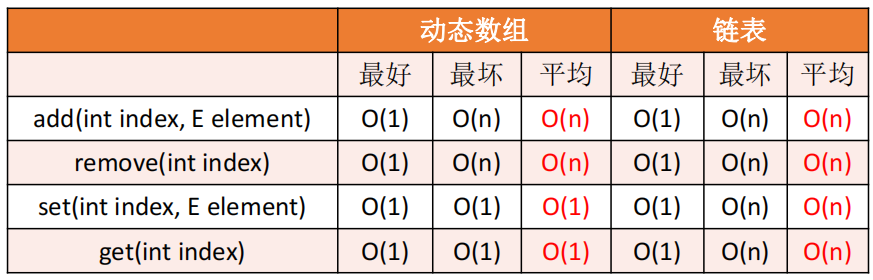
在这里插入图片描述

🎉 这里的链表是单链表

四、动态数组 add(E element) 复杂度分析

在这里插入图片描述

🎉 扩容操作不是每次都会发生

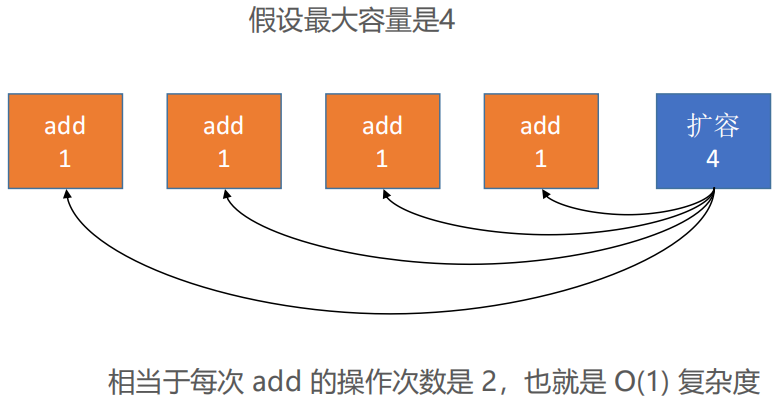
在这里插入图片描述

什么情况下适合使用均摊复杂度？
🎉经过连续的多次复杂度比较低的情况后，出现个别复杂度比较高的情况

五、动态数组的缩容

🎁 如果内存使用比较紧张，动态数组有比较多的剩余空间，可以考虑进行缩容操作

🎁 比如剩余空间占总容量的一半时，就进行缩容（size 大于总容量的一半的时候进行缩容）

🎁 缩容操作在动态数组的删除方法中进行

  private void trim() {
       int oldCapacity = elements.length;
       int halfCapacity = oldCapacity >> 1;
       // size 大于总容量的一半, 总容量小于等于默认容量的时候不缩容
       if (size >= halfCapacity || oldCapacity <= DEFAULT_CAPACITY) return;

       E[] newElements = (E[]) new Object[halfCapacity];

       for (int i = 0; i < size; i++) {
           newElements[i] = elements[i];
       }

       elements = newElements;

       System.out.println(oldCapacity + "缩容为" + halfCapacity);
   }