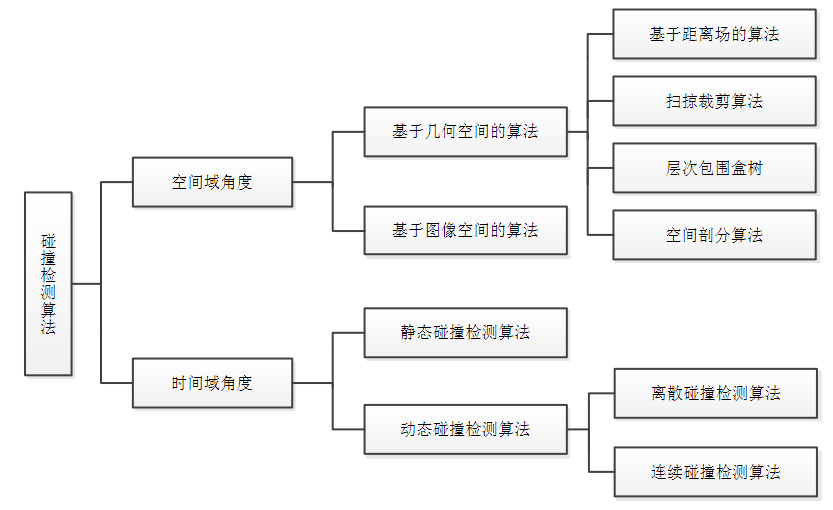
算法的分类
目录
一、基于空间域的碰撞检测算法分类
1. 基于图像空间的碰撞算法
2.基于几何空间的碰撞检测算法
(1)基于空间剖分算法
(2)裁剪扫掠法
(3)基于距离场的算法
(4)基于层次包围盒的算法
① 轴向包围盒
② 球包围盒
③ 方向包围盒
④ 离散方向多面体
一、基于空间域的碰撞检测算法分类
从空间域角度出发,碰撞检测算法可以分为基于图像空间和基于几何空间的碰撞检测算法, 两者的区别是前者将图形硬件作为辅助来解决碰撞检测问题,后者则利用几何领域的理论知识 来解决碰撞检测问题。
1. 基于图像空间的碰撞算法
基于图像空间的碰撞算法利用图形硬件将模型投影到二维平面空间,再根据这些投影的相 交情况和模型的各类缓存信息来判断模型之间是否碰撞。
优点:
1)碰撞检 测过程不需要进行任何预处理,比较适合多柔体模型的环境;
2)对于同样复杂度的场景, 算法的效率没有大的变化,稳定性比较高;
3)利用 GPU 加速图形的渲染,降低了 CPU 的计算 负荷,提高了算法的效率。
缺点:
1)图像的分辨率的高低会影响算 法的精确度,可能会出现误判情况;
2)不适合处理凹体之间的碰撞检测问题;
3)需要解决图 形硬件和 CPU 的负载均衡问题。
2.基于几何空间的碰撞检测算法
常见的主要有以下几类算法:基于 空间剖分的算法、基于扫掠和裁剪的算法、基于层次包围盒树的算法以及基于距离场的算法等。
(1)基于空间剖分算法
依据一定的规则将场景划分成不同的区域,在碰撞检测时只需对位于同 一区域或者相邻区域的模型之间进行检测,这样可以大大减少组合测试的数量,从而提高分离 测试阶段的效率。
算法中通常使用的数据结构有均匀网格、8 叉树、k-d 树以及 BSP 树等。
均匀网格表示将场景空间划分成多个大小一致的单元, 使得每个对象都与其所属的单元格关联,则组合测试将限定在位于同一网格单元的模型之间, 此类算法的性能主要受网格单元的尺寸的影响,最坏的情况下,场景中所有的模型均位于一个 网格中,此时算法的时间复杂度为 O(n2)。
8 叉树属于一种空间层次结构划分方案,其划分方法 是首先沿 X、Y 和 Z 轴将场景划分成 8 个等大的立方体,每个立方体对应根节点的一个子节点, 对于每个子节点,若其中的模型数量超过了设定的阈值,则对这个子节点再以同样的方法递归 划分。
与 8 叉树的在空间坐标轴上的同步划分方式不同,k-d 树在一次操作过程中只沿其中的 一条轴进行划分,其划分轴信息一般用两个二进制存储于树的节点中。
BSP 树又称二分空间划 分树,其结构为 2 叉树,对于 n 维空间,它采用任意的 n-1 超平面递归将空间划为多个子空间 对,在大多数场景中,BSP 树均可达到 k-d 树及 8 叉树的效果,反之一般不成立。
(2)裁剪扫掠法
该算法主要基于这样一个理论:任意两个在三维空间相交的模型,则它们在空间坐标轴上的投 影也一定相交。裁剪扫掠法的检测过程如下:首先计算出每个模型的包围盒,包围盒在每个坐 标轴上均对应一个区间[a,b],然后将 n 个此类区间的边界值 a 和 b 插入到一个排序表中,最 后对上述排序进行扫掠,遇到 a 值时,将对应的区间加入到一个临时新建的表中;遇到 b 时, 将在临时表中对应的区间移除,每当一个新的区间加入到表中时,可以判断此区间与临时表中 原有的区间重合。
上文介绍的两种几何空间的碰撞检测算法主要适用于多模型场景的粗略测试阶段,下面介 绍两种适用于逐步求精阶段的碰撞检测算法:基于距离场的算法以及基于层次包围盒的算法。
(3)基于距离场的算法
距离场表示物体表面某个区域内所有点与此物体的最短距离,最短距离的值可以用正负符号修饰,表示某一点位于模型内部还是模型外部。
(4)基于层次包围盒的算法
基于层次包围盒的碰撞检测算法最初是由包围盒技术发展而来,包围盒技术的原理是以规 则较大的包围盒来代替不规则较小的模型进行相交检测,快速剔除物体不相交的情况。
常 见的包围盒主要有以下几类:轴向包围盒(AABB)、球包围盒(Sphere)、方向包围盒(OBB) 和离散方向多面体(k-dop)等
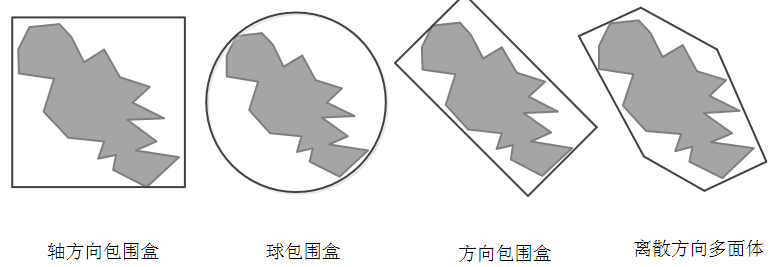
① 轴向包围盒
它可以表示为三维空间中三条边均与空间坐标轴平行的长方体。
表达式
给定 AABB 的中心点 c 和三条边的半径𝑟𝑥 ,𝑟𝑦 ,𝑟𝑧,AABB 所包含的区域可以用 以下公式定义:
𝑅 = {|𝑥, 𝑦, 𝑧 ||𝑐. 𝑥 − 𝑥 |≤ 𝑟𝑥 , |𝑐. 𝑦 − 𝑦| ≤ 𝑟𝑦 , |𝑐. 𝑧 − 𝑧 |≤ 𝑟𝑧 }
相交测试
只需 6 次比较运算操作即可判断两个 AABB 是否相交: 如果两个 AABB 在 X、Y 以及 Z 轴上的投影都相交,那么两个 AABB 相交,否则分离。
② 球包围盒
与其它包围盒相比,球包围盒(Sphere)是一类紧密性相对较差的包围盒,其优点是可以 实现快速相交测试,以及在对模型的球包围盒重构时不用考虑模型的旋转变换。
表达式
一般只需给定球的球心 c 以及半径 r:
𝑅 = {𝑥, 𝑦, 𝑧 (𝑥 − 𝑐. 𝑥)2 + (𝑦 − 𝑐. 𝑦)2 + (𝑧 − 𝑐. 𝑧)2 ≤ 𝑟2}
相交测试
球包围盒之间的相交测试也非常简单,只需计算两个球心的距离,然后与 两个包围盒的半径和进行比较,由于计算机中求根运算操作所消耗的时间要远远多于求平方的 操作,实际上一般使用距离的平方值来进行比较。
③ 方向包围盒
相交测试
最常见的 一种方法是通过判断两个包围盒之间是否存在分离轴来确定它们之间是否相交,若空间存在一 条直线,两个包围盒在这条直线上的投影分离,那么两个包围盒之间分离。任意两个 OBB 之 间一共存在 15 条潜在的分离轴,逐一检测完这 15 条轴是一个比较复杂的过程。
④ 离散方向多面体
离散方向多面体(K-DOP)是一种典型的凸多面体,它可以定义为多个平行平面之间的交 集,其中 K 表示 K-DOP 所有面的外法向量的数目,即 K-DOP 的方向轴的数量为 K/2。