深度优先搜索包含一个递归,对其进行分析要复杂一些。与上一篇文章一样,还是给节点定义几个状态,然后详细分析深度优先搜索算法有哪些性质。
算法描述
定义状态
- v . c o l o r :初始状态为白色,被发现时改为灰色,其所有的邻接节点遍历完成后,变为黑色。 v.color:初始状态为白色,被发现时改为灰色,其所有的邻接节点遍历完成后,变为黑色。 v.color:初始状态为白色,被发现时改为灰色,其所有的邻接节点遍历完成后,变为黑色。
- v . π : v 的前驱节点,也就是说是从哪个节点发现 v 的,初始化为 n i l v.\pi : v 的前驱节点,也就是说是从哪个节点发现 v 的,初始化为 n i l v.π:v的前驱节点,也就是说是从哪个节点发现v的,初始化为nil
- v . d :时间戳,表示节点第一次被发现的时间 v.d:时间戳,表示节点第一次被发现的时间 v.d:时间戳,表示节点第一次被发现的时间
- v . f :时间戳,表示完成对邻接节点扫描的时间 v.f :时间戳,表示完成对邻接节点扫描的时间 v.f:时间戳,表示完成对邻接节点扫描的时间
DFS(G)
for v in G.V
v.color=white
v.Π=nil
time=0
for v in G.V
if v.color == white
DFS-VISIT(G, v)
DFS-VISIT(G, v)
time += 1;
v.d = time
v.color = grary
for u in G.Adj[v]:
if u.color = white:
u.Π=v
DFS-VISIT(G, u)
v.color = black
time += 1;
v.f = time;
该算法的时间复杂度分析与广搜的分析类似,使用聚合分析,发现每个节点访问一次,每条边访问一次,总复杂度为 O ( V + E ) O(V+E) O(V+E)
深度优先搜索的性质
深度优先搜索提供了关于图结构价值很高的信息。
性质1:生成的前驱子图
G
.
π
G.\pi
G.π 是由多颗树构成的森林。
- u = v . π u=v.\pi u=v.π,当且仅当DFS-VISIT(G, v) 在对 u 节点邻接表搜索时被调用。
- v 是节点 u的后代,当且仅当节点 v 在节点u 为灰色时被发现
性质2:括号化结构:对于某一个节点,u, 如果以’(u’表示节点u的发现,’u)'表示节点u的完成。则算法的运行过程会形成一个恰当嵌套的括号化结构。
定理1. 括号化定理:在对图G进行深度优先搜索时,任意两个节点v,u,下面三种情况只有一种成立
- 区间 [ u . d , u . f ] [u.d, u.f] [u.d,u.f]和区间 [ v . d , v . f ] [v.d, v.f] [v.d,v.f]完全分离, v v v, u u u之间没有后代关系。
- 区间 [ u . d , u . f ] [u.d, u.f] [u.d,u.f] 在 区间 [ v . d , v . f ] [v.d, v.f] [v.d,v.f] 之内。在 深度优先搜索树 中, u u u 是 v v v 的后代
- 区间 [ v . d , v . f ] [v.d, v.f] [v.d,v.f] 在 区间 [ u . d , u . f ] [u.d, u.f] [u.d,u.f] 之内。在 深度优先搜索树 中, v v v 是 u u u 的后代
证明:当
u
.
d
<
v
.
d
u.d \lt v.d
u.d<v.d 时,根据
u
.
f
u.f
u.f 与
v
.
d
v.d
v.d的关系,可以分为两种情况
u
.
f
<
v
.
d
u.f \lt v.d
u.f<v.d 时,容易扩充得到不等式
u
.
d
<
u
.
f
<
v
.
d
<
v
.
f
u.d \lt u.f \lt v.d \lt v.f
u.d<u.f<v.d<v.f,此时两区间分离,且没有一个节点是在另一个节点是灰色时被发现的,一次没有任何一个节点是另一个节点的后代
u
.
f
>
v
.
d
u.f \gt v.d
u.f>v.d,说明节点
v
v
v在节点
u
u
u是灰色时被发现。意味着v 是u 的后代。此外,当算法返回来继续处理
u
u
u时,
v
v
v节点已经处理完,因此区间
[
v
.
d
,
v
.
f
]
[v.d, v.f]
[v.d,v.f] 在 区间
[
u
.
d
,
u
.
f
]
[u.d, u.f]
[u.d,u.f] 之内。 证明完毕
推论:在深度优先树中,
v
v
v 是
u
u
u 的后代,当且仅当
u
.
d
<
v
.
d
<
v
.
f
<
u
.
f
u.d \lt v.d \lt v.f \lt u.f
u.d<v.d<v.f<u.f成立
定理2:白色路径定理。
v
v
v 是
u
u
u 的后代,当且仅当 算法发现
u
u
u 时,存在一条从
u
u
u 到
v
v
v 的全部由白色节点组成的路径。
证明:
v
v
v 是
u
u
u的后代时,
v
v
v 在
u
u
u 之后被发现。发现
u
u
u 时,
u
u
u 的后代此时均未被发现为白色,当然包括
v
v
v。所以可以顺着后代路径,找到一条达到
v
v
v 的白色路径。
当发现
u
u
u 时,存在一条从
u
u
u 到
v
v
v 的白色路径。意味着深度优先算法至少一定会 完成
v
v
v 的访问后,再回到
u
u
u。满足不等式,
u
.
d
<
v
.
d
<
v
.
f
<
u
.
f
u.d \lt v.d \lt v.f \lt u.f
u.d<v.d<v.f<u.f。符合定理1的后两条之一。因此充分性和必要性均得证。
性质3:边的分类
根据深度优先搜索森林 G . π G.\pi G.π,可以定义 4 种边类型。
- 树边: G . π G.\pi G.π 中的边
- 后向边:当v是u的祖先时, ( u , v ) (u, v) (u,v) 称为后向边
- 前向边:当v是u的祖先时, ( v , u ) (v, u) (v,u) 称为前向边
- 横向边:其他的所有边。
深度优先搜索算法可以将图中的所有边进行分类:当探索边 ( v , u ) (v, u) (v,u)时
- u u u 是 白色, ( v , u ) (v,u) (v,u)是树边
- u u u 是 灰色, ( v , u ) (v,u) (v,u)是后向边
-
u
u
u 是 黑色,
(
v
,
u
)
(v,u)
(v,u)是前向边或横向边
- 当 u . d < v . d u.d\lt v.d u.d<v.d 时, ( v , u ) (v,u) (v,u)是前向边
- 当 u . d > v . d u.d\gt v.d u.d>v.d 时, ( v , u ) (v,u) (v,u)是横向边
无向图的边类型按照符合的第一顺位分类。
定理3:无向图的边,要么是树边,要么是后向边。
证明:设
(
u
,
v
)
(u, v)
(u,v) 时无向图的一条边。假设
u
.
d
<
v
.
d
u.d < v.d
u.d<v.d,
u
u
u 先被访问。
v
v
v 在
u
u
u 的邻接节点链表里。但算法第一次访问边
(
u
,
v
)
(u, v)
(u,v) 时,仍然有两种可能:如果从
v
v
v 访问
u
u
u,此时
u
u
u 已经被发现,
(
u
,
v
)
(u, v)
(u,v) 是一条后向边。如果从
u
u
u 访问
v
v
v,
v
v
v 一定是白色。因为如果是灰色或者黑色,那么
(
u
,
v
)
(u, v)
(u,v) 一定已经从
v
v
v 访问过了。因此
(
u
,
v
)
(u, v)
(u,v) 此时是树边。
强连通分量
这应该是图论中第一个简单(只用到了深搜)有用,但是难想,不直观的算法了。
首先定义强连通分量:图G的强连通分量是一个最大的节点集合
C
⊆
G
.
V
C \subseteq G.V
C⊆G.V,该集合中的任意两个节点之间都可以相互到达。下图中圈起来的节点,就是强连通分量
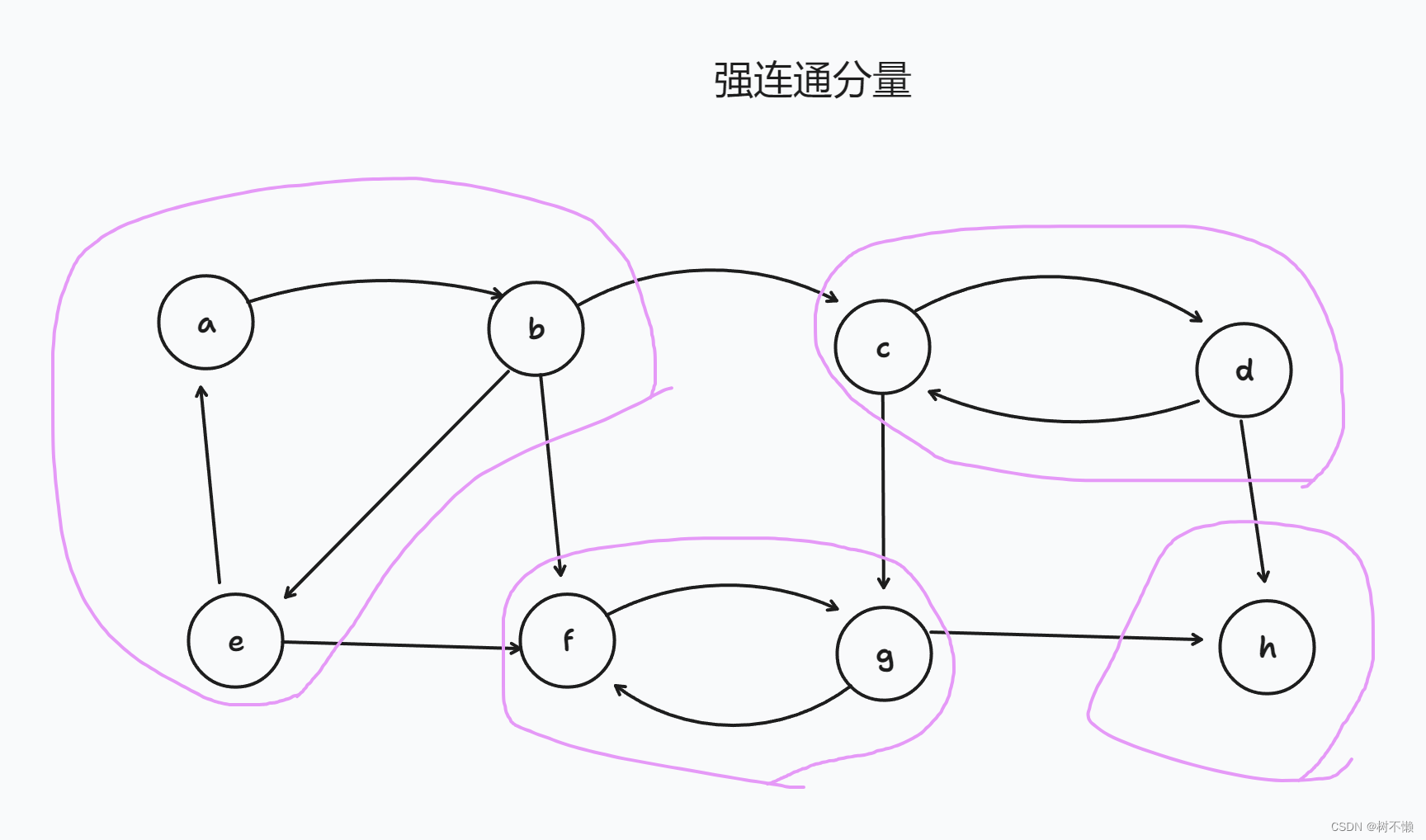
为了实现强连通分量算法,先讨论一下分量图:
G
S
C
C
=
(
V
S
C
C
,
E
S
C
C
)
G^{SCC} = (V^{SCC}, E^{SCC})
GSCC=(VSCC,ESCC)。定义如下:假如 G 由强连通分量
C
1
,
C
2
,
.
.
.
,
C
k
C_1, C_2,..., C_k
C1,C2,...,Ck,易知强连通分量之间并不相交。任意从分量中挑出代表节点
v
1
,
v
2
,
.
.
.
,
v
k
v_1, v_2, ..., v_k
v1,v2,...,vk 作为
V
S
C
C
V^{SCC}
VSCC。如果对于两个节点
x
∈
C
x
,
y
∈
C
y
x\in C_x, y\in C_y
x∈Cx,y∈Cy,存在边
(
x
,
y
)
(x, y)
(x,y),则边
(
v
x
,
v
y
)
(v_x, v_y)
(vx,vy) 在
E
S
C
C
E^{SCC}
ESCC中。上面的分量图可以通过缩点变成分量图如下:
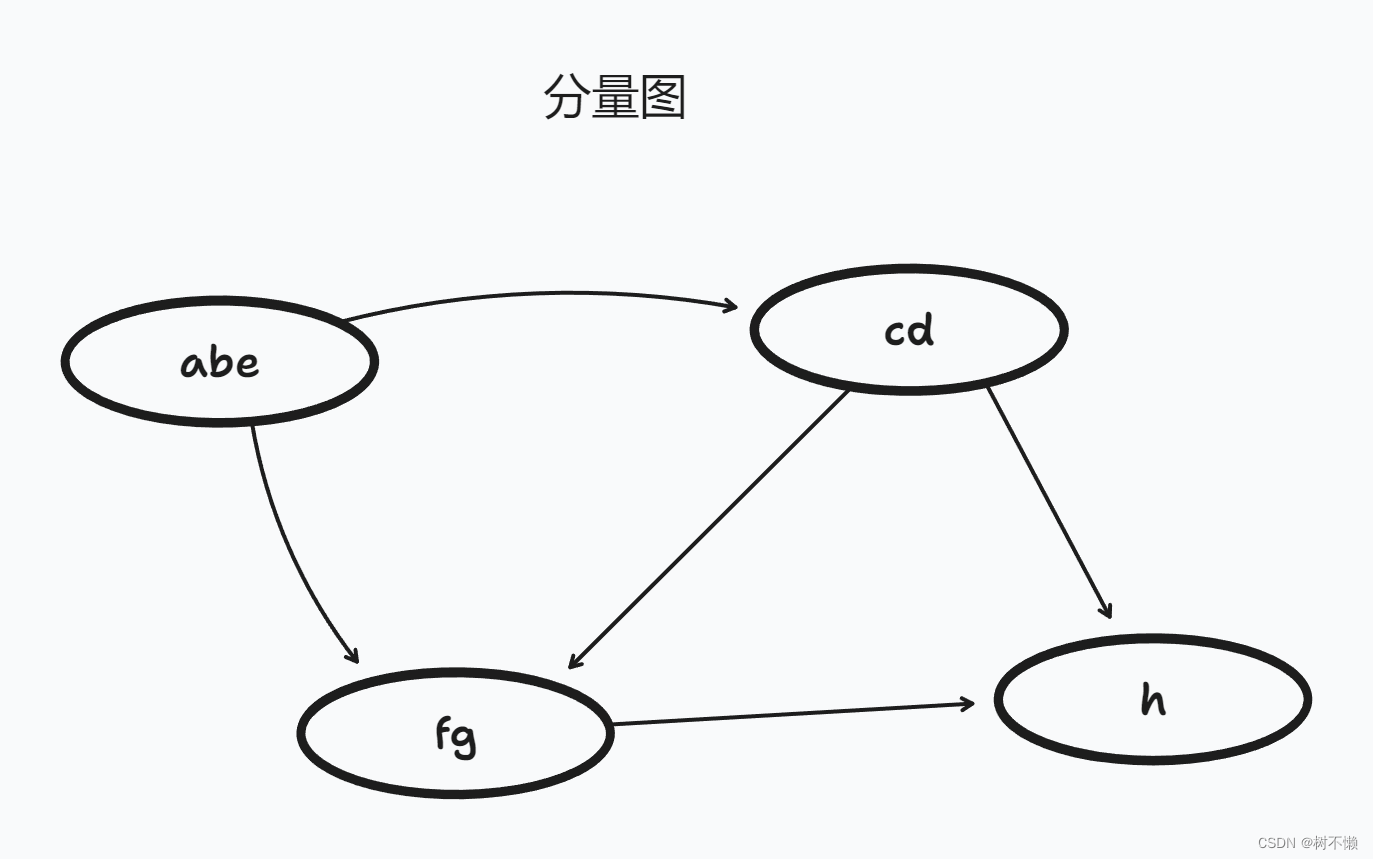
定理4 :分量图是有向无环图:设
C
C
C 和
C
′
C'
C′是两个不同的强连通分量,设
u
,
v
∈
C
u,v\in C
u,v∈C,
u
′
,
v
′
∈
C
′
u',v'\in C'
u′,v′∈C′。如果存在一条边
(
u
,
u
′
)
(u, u')
(u,u′),则必不存在边
(
v
′
,
v
)
(v',v)
(v′,v)。
证明:如果存在边$(v’,v),那么
C
,
C
′
C, C'
C,C′ 两个强连通分量里的节点便满足了强连通分量的定义,
C
,
C
′
C, C'
C,C′ 应该合并成 1 个,而不是两个,矛盾。
为了不产生歧义,对节点的描述 v . f v.f v.f 表示的都是 对 G G G 深度优先遍历的结果,而不是 G T G^T GT
定理5:(深度优先搜索的节点完成时间) :设
C
C
C 和
C
′
C'
C′是图
G
G
G的两个不同的强连通分量,
f
(
C
)
f(C)
f(C)表示强连通分量
C
C
C 的节点
v
.
f
v.f
v.f 的最大值,
d
(
C
)
d(C)
d(C)表示强连通分量
C
C
C 的节点
v
.
d
v.d
v.d 的最小值。如果存在一条边
(
u
,
v
)
∈
G
.
E
(u,v) \in G.E
(u,v)∈G.E满足
u
∈
C
u\in C
u∈C,
v
∈
C
′
v\in C'
v∈C′,那么
f
(
C
)
>
f
(
C
′
)
f(C) > f(C')
f(C)>f(C′).
证明:根据深度优先搜索中,最先发现的节点在 C 中还是 C’ 中进行讨论。
- 如果 d ( C ) < d ( C ′ ) d(C) \lt d(C') d(C)<d(C′),那么深度优先搜索算法一定会通过 边 ( u , v ) (u, v) (u,v) 遍历完 C ′ C' C′ 中的节点后,在回到 C C C 中。因此 f ( C ) > f ( C ′ ) f(C) > f(C') f(C)>f(C′).
- 如果 d ( C ) > d ( C ′ ) d(C) \gt d(C') d(C)>d(C′),那么由于 分量图是无环图,将无法通过 C ′ C' C′ 到达 C C C中的任何一个节点。必然是算法返回 DFS 主循环后,再访问 C C C 中的节点,此时仍有 f ( C ) > f ( C ′ ) f(C) > f(C') f(C)>f(C′) 证毕。
推论5.1:设
C
C
C 和
C
′
C'
C′是图
G
G
G的两个不同的强连通分量,如果存在一条边
(
u
,
v
)
∈
G
T
.
E
(u,v) \in G^T.E
(u,v)∈GT.E,满足
u
,
v
∈
C
u,v\in C
u,v∈C,
u
′
,
v
′
∈
C
′
u',v'\in C'
u′,v′∈C′,那么
f
(
C
)
<
f
(
C
′
)
f(C) < f(C')
f(C)<f(C′).
根据定理5 以及下图,本推论有较为直观的理解,不再证明。
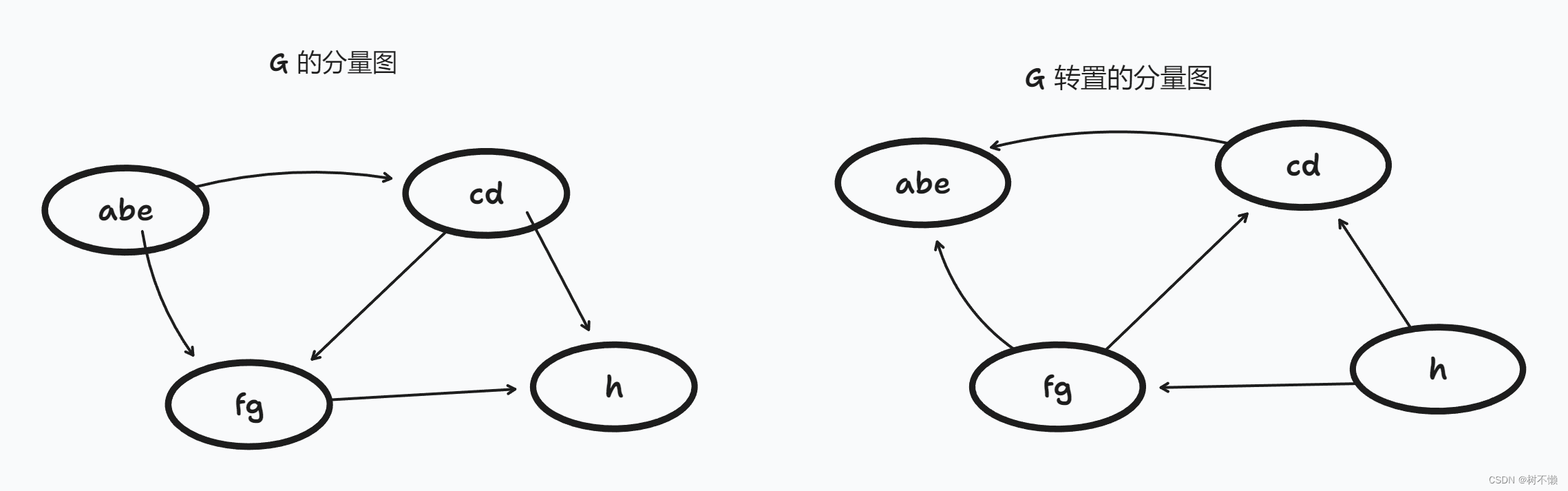
强连通分量算法
strongly-connected-components(G)
DFS(G) // 计算出 v.f
compute GT // 计算转置图,节点列表按照 v.f 降序排列
DFS(GT)
print GT 的深度优先搜索森林。
定理6 强连通分量算法正确
证明: 数学归纳法:归纳假设是 算法第三行运行时,生成的前 k 棵树是强连通分量。初始情况 k = 0,显然成立。
假设前
k
k
k 棵树是强连通分量,考虑第
(
k
+
1
)
(k + 1)
(k+1) 棵树。树跟节点为
u
u
u ,
u
u
u 位于强连通分量
C
C
C 中。由于
u
u
u是根节点,对于除
C
C
C 外的未被访问的任意 强连通分量
C
′
C'
C′,有
u
.
f
=
f
(
C
)
>
f
(
C
′
)
u.f = f(C) \gt f(C')
u.f=f(C)>f(C′)。根据归纳假设
C
C
C 当前所有的节点都是白色。根据白色路径定理,
C
C
C 中的所有其他节点都是
u
u
u 的后代。根据推论 5.1,任何从 C 出发的边,一定通向
f
(
C
b
)
f(C^b)
f(Cb) 更大连通分量
C
b
C^b
Cb。因此根据我们的遍历顺序,除
C
C
C内的节点外,不存在节点能够成为
u
u
u 的后代。因此
k
+
1
k+1
k+1 棵树刚好形成一个强连通分量。归纳 完毕。
可以从 G T G^T GT 的分量图角度来看待第二次深度优先遍历。就相当于逆着 G T G^T GT 的分量图的拓扑序来遍历,看上面的右图更直观。
给出求强连通分量的 C++ 代码做参考
int V;
vector<int> G[MAX_V];
vector<int> Gt[MAX_V];
vector<int> vs;
bool used[MAX_V];
int cmp[MAX_V]; // 表示 节点 v 所属强连通分量的拓扑序编号
void add_edge(int from, int to) {
G[from].push_back(to);
Gt[to].push_back(from);
}
void dfs(int v) {
used[v] = true;
for (int i = 0; i < G[v].size(); i++) {
if (!used[G[v][i]) dfs(G[v][i]);
}
vs.push_back(v);
}
void rdfs(int v, int k) {
used[v] = true;
cmp[v] = k;
for (int i = 0; i < Gt[v].size(); i++) {
if (!used[v]) dfs(Gt[v][i])
}
}
int scc() {
memset(used, 0, sizeof(used));
for (int v = 0; v < V; v++) {
if(!used[v]) dfs(v);
}
memset(used, 0, sizeof(used));
int k = 1;
for (int v = V - 1; v >= 0; v--) {
if(!used[vs[v]]) rdfs(vs[v], k++);
}
return k; // 表示有几组强连通分量
}
至此,应该可以说搞懂图的深度优先搜索了。