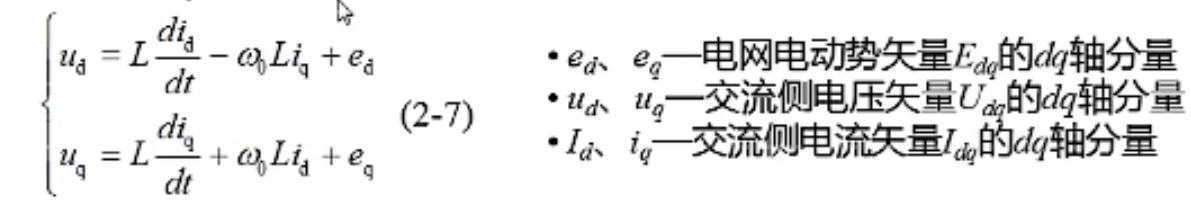Problem - 1805D - Codeforces

给定一棵包含n个节点的树(一个无环联通图),对于一个固定的整数k,定义Gk为一个具有n个节点的无向图,其中只有当在给定树中节点u和v之间的距离至少为k时才存在边。
对于从1到n的每个k,请打印图Gk中连通分量的数量。
输入:第一行包含整数n(2≤n≤105)- 图中节点的数量。
接下来的(n-1)行,每行包含两个整数u和v(1≤u,v≤n),表示树中u和v之间有一条边。保证这些边构成一棵有效的树。
输出:输出n个整数:对于从1到n的每个k,输出图Gk中连通分量的数量。
Examples
Input
Copy
6 1 2 1 3 2 4 2 5 3 6
Output
Copy
1 1 2 4 6 6
Input
Copy
5 1 2 2 3 3 4 3 5
Output
Copy
1 1 3 5 5
在第一个例子中:如果k=1,图中每对顶点之间都有一条边,因此它有一个连通分量。如果k=4,则图仅具有边4↔6和5↔6,因此图有4个连通分量。
在第二个例子中:当k=1或k=2时,图只有一个连通分量。当k=3时,图Gk分裂成3个连通分量:一个连通分量包含顶点1、4和5,另外两个连通分量各包含一个顶点。当k=4或k=5时,每个顶点都是一个单独的连通分量。
题解:
说到树,又说到节点之间的距离,我们应该想到树的直径
树的直径可以通过两次dfs求得
得到树的直径得两个端点后,我们可以知道一个点,到最远端点的距离,
对于k,所有距离>=k的节点,都会属于同一个联通块
因为这些点一定与一个直径端点链接,而两个直径端点也一定链接
因此我们只需要对所有节点的距离排个序,找出每次找出多少个小于k的ans
ans + 1就是答案
唯一需要注意的是,如果有n个节点小于此时的k,肯定不用加那个1了
#include <cstdio>
#include <cstring>
#include <algorithm>
#include<iostream>
#include<vector>
#include<set>
#include<map>
#include<cmath>
#include<queue>
using namespace std;
typedef long long ll;
#define int long long
typedef pair<int,int> PII;
typedef unsigned long long ULL;
const int N = 4e5 + 10;
int mod = 1e9 + 7;
vector<int> p[N];
int now;
int dep[N];
int dis[N];
void dfs(int x,int fa)
{
if(dep[x] > dep[now])
{
now = x;
}
for(auto ne:p[x])
{
if(ne == fa)
continue;
dep[ne] = dep[x] + 1;
dfs(ne,x);
}
}
void dfs1(int x,int fa,int cnt)
{
dis[x] = max(dis[x],cnt);
for(auto ne:p[x])
{
if(ne == fa)
continue;
dfs1(ne,x,cnt + 1);
}
}
void solve()
{
int n;
cin >> n;
for(int i = 1;i < n;i++)
{
int x,y;
cin >> x >> y;
p[x].push_back(y);
p[y].push_back(x);
}
now = 1;
dfs(1,0);
int p = now;
dfs(now,0);
int q = now;
dfs1(p,0,0);
dfs1(q,0,0);
sort(dis + 1,dis + 1 + n);
for(int i = 1;i <= n;i++)
{
int l = 0,r = n;
while(l <= r)
{
int mid = (l + r)/2;
if(dis[mid] >= i)
{
r = mid - 1;
}
else
{
l = mid + 1;
}
}
if(l > n)
l--;
cout << l <<" ";
}
}
signed main()
{
ios::sync_with_stdio(0 );
cin.tie(0);cout.tie(0);
int t = 1;
// cin >> t;
while(t--)
{
solve();
}
}