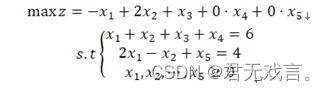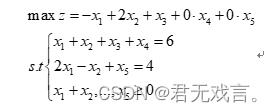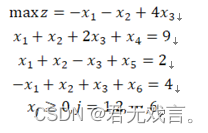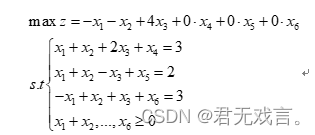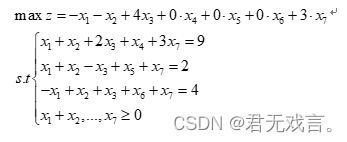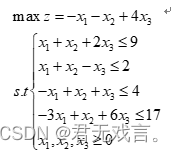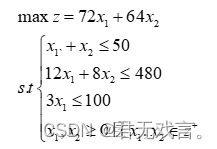| 一、实验目的: 1. 掌握用MATLAB、LINGO 、EXCEL优化工具箱解线性规划的方法; 2. 练习建立实际问题的线性规划模型; 3. 掌握线性规划灵敏度分析原理; 4. 预习线性规划的灵敏度分析原理及方法。 | ||||||||
| 二、实验内容 题目1:求解线性规划问题,并进行灵敏度分析。
数学模型: (1)
(2)
程序代码: (1) MODEL: MAX=4*x1+2*x2+x3+0*x4+0*x5; x1+x2+x3+x4=6; 2*x1-x2+x5=4; END (2) MODEL: MAX=-x1+2*x2+x3+0*x4+0*x5; x1+x2+x3+x4=6; 2*x1-x2+x5=4; END 程序执行结果: (1)
(2)
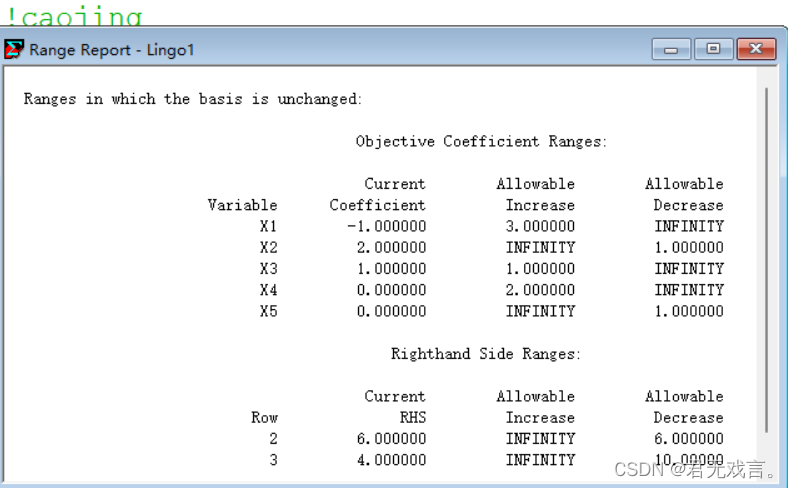
结果解释: 由-1变为 4时,新问题的最优解为Z=18.66667(第一问答案),其中,x1=3.333333,x2=2.666667,x3=x4=x5=0。 reduced cost结果解释(2): 变量x1对应的reduced cost值为3,表示当非基变量x1的值从0变为 1时(此时假定其他非基变量保持不变),最优目标值为 z= 18.66667+3 = 21.66667。同理(以下均其他非基变量保持不变),X3增加一个单位时,最优目标值增加1,4增加一个单位时,最优目标值增加2,X2,x5的值变化对最优值无影响。 Slack or Surplus结果解释(2): Slack or Surplus值为给出的松驰变量值,可以看出对于约束1(即第一个不等式)松弛变量为12,约束2和约束3中的变量值刚好达到约束条件。 Dual price结果解释(2): Dual price值为对偶价格,表示当对应约束有微小变动时, 目标函数的变化率。 显然,第一个约束的右端值增加1个单位目标将增加1个单位,对于约束二,右端值增加1个单位目标值将增加2个单位,对于约束三,对偶价格为0 目标函数系数和约束条件右端常数项的灵敏度分析: Objective Coefficient Ranges(2)结果分析: 对于x1来说,目标函数中原来的系数为-1,允许增加(Allowable Increase)3、或者允许减少(Allowable Decrease)到无穷小,说明当它在[-∞,-1+3]=[ -∞,2]范围变化时,最优基保持不变。同理,x2系数 在(第二问答案),x3系数在 ,x4系数在 ,x5系数在 时,最优解不变。 Right hand Side Ranges (2)结果分析: Row=2的行Current RHS值为6即第2行约束中右端项,当它在[6-6,6+∞] = [0,+∞]范围变化时,最优基保持不变。同理,第三行约束右端项在[-6,+∞] 最优基保持不变 题目2:求解线性规划问题,并进行灵敏度分析。
若右端向量从 ,求新问题的最优解。 数学模型:
程序代码: MODEL: MAX=-x1-x2+4*x3; x1+x2+2*x3+x4=3; x1+x2-x3+x5=2; -x1+x2+x3+x6=3; END 程序执行结果:
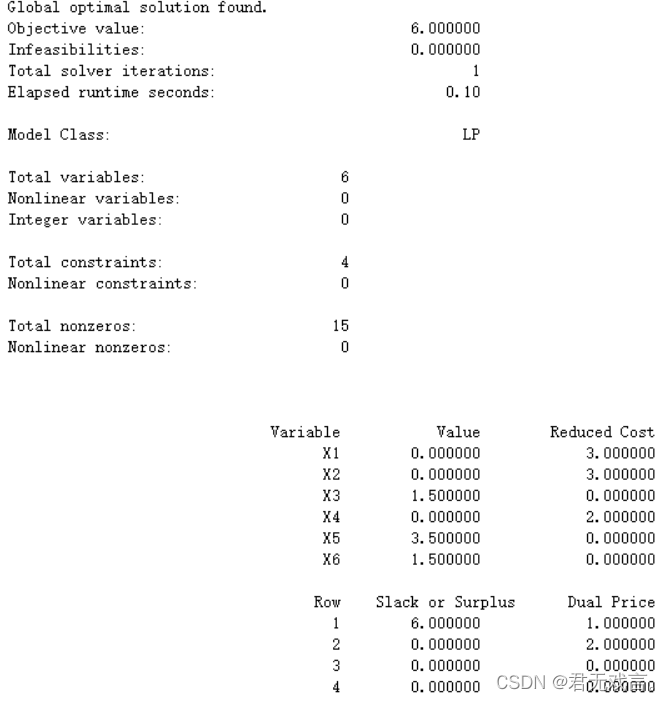
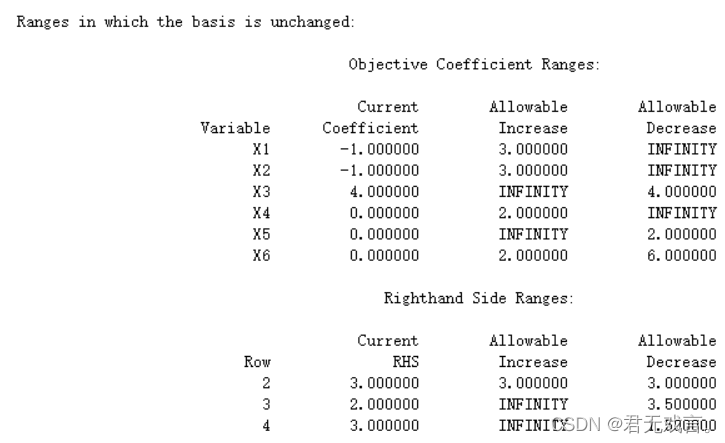
结果解释: 由题目1分析同理可知,当x3=1.5,x5=3.5,x6=1.5,x1=x2=x4=0时,取得最优值Z=6(问题答案) reduced cost结果解释: x1增加一个单位最优目标值增加3,x2增加一个单位最优目标值增加3,x4增加一个单位时,最优目标值增加2。X3,x5,x6的值变化对最优值无影响。 Slack or Surplus结果解释: 可以看出对于约束1松弛变量为6,约束2,3,4中的变量值刚好达到约束条件。 Dual price结果解释: 第一个约束的右端值增加1个单位目标将增加1个单位,对于约束二,右端值增加1个单位目标值将增加2个单位,对于约束3,4,对偶价格为0 目标函数系数和约束条件右端常数项的灵敏度分析: Objective Coefficient Ranges结果分析:
Right hand Side Ranges 结果分析:
题目3:求解线性规划问题,并进行灵敏度分析。
现增加一个新变量 数学模型:
程序代码: MODEL: MAX=-x1-x2+4*x3+3*x7; x1+x2+2*x3+x4+3*x7=9; x1+x2-x3+x5+x7=2; -x1+x2+x3+x6-3*x7=4; END 程序执行结果:
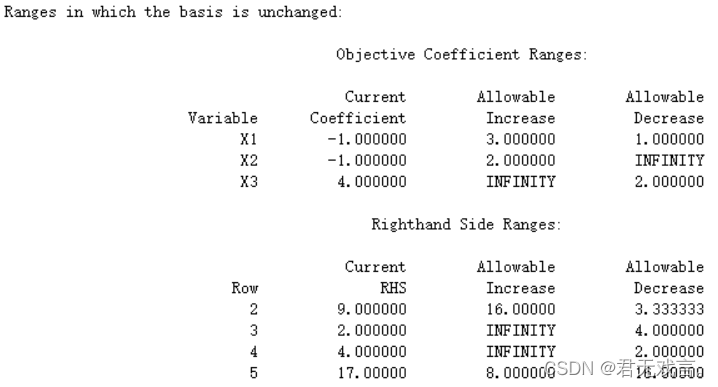
结果解释: 由题目1分析同理可知,当x3=4.33333,x5=6.222222,x7=0.1111111,x1=x2=x4=x6=0时,取得最优值Z=17.66667(问题答案) reduced cost结果解释: x1增加一个单位最优目标值增加2,x2增加一个单位最优目标值增加3.333333,x4增加一个单位最优目标值增加1.666667 ,x6增加一个单位最优目标值增加0.666667。X3,x5,x7的值变化对最优值无影响。 Slack or Surplus结果解释: 可以看出对于约束1松弛变量为17.667,约束2,3,4中的变量值刚好达到约束条件。 Dual price结果解释: 第一个约束的右端值增加1个单位目标将增加1个单位,对于约束二,右端值增加1个单位目标值将增加1.666667个单位,对于约束四,右端值增加1个单位目标值将增加0.666667个单位,对于约束3对偶价格为0 目标函数系数和约束条件右端常数项的灵敏度分析: Objective Coefficient Ranges结果分析:
Right hand Side Ranges 结果分析:
题目4:求解线性规划问题,并进行灵敏度分析。
现增加新约束: 数学模型:
程序代码: MODEL: MAX=-x1-x2+4*x3; x1+x2+2*x3<9; x1+x2-x3<2; -x1+x2+x3<4; -3*x1+x2+6*x3<17; END 程序执行结果:
结果解释: 同理可知,当x1=1.666667,x2=0,x3=3.666667时,取得最优值Z=13。(问题答案) reduced cost结果解释: x2增加一个单位最优目标值增加2。x1,x3的值变化对最优值无影响。 Slack or Surplus结果解释: 可以看出对于约束1松弛变量为13,对于约束3松弛变量为4,对于约束4松弛变量为2,约束2,5中的变量值刚好达到约束条件。 Dual price结果解释: 第一个约束的右端值增加1个单位目标将增加1个单位,对于约束二,右端值增加1个单位目标值将增加0.5个单位,对于约束五,右端值增加1个单位目标值将增加0.5个单位,对于约束三和约束四对偶价格为0 目标函数系数和约束条件右端常数项的灵敏度分析:
题目5: 建立模型并求解:一奶制品加工厂用牛奶生产A1,A2两种奶制品,1桶牛奶可以在甲车间用12小时加工成3公斤A1,或者在乙车间用8小时加工成4公斤A2。根据市场需求,生产的A1,A2全部能售出,且每公斤A1获利24元,每公斤A2获利16元。现在加工厂每天能得到50桶牛奶的供应,每天正式工人总的劳动时间480小时,并且甲车间每天至多能加工100公斤A1,乙车间的加工能力没有限制。试为该厂制订一个生产计划,使每天获利最大,并进一步讨论以下3个附加问题: (1)若用35元可以买到1桶牛奶,应否作这项投资?若投资,每天最多购买多少桶牛奶? (2)若可以聘用临时工人以增加劳动时间,付给临时工人的工资最多是每小时几元? (3)由于市场需求变化,每公斤A1的获利增加到30元,应否改变生产计划? 数学模型:设用x1桶牛奶制成了3x1公斤的A1,用x2桶牛奶制成了2x2公斤的A2,其中x1和x2均为整数。 (1)
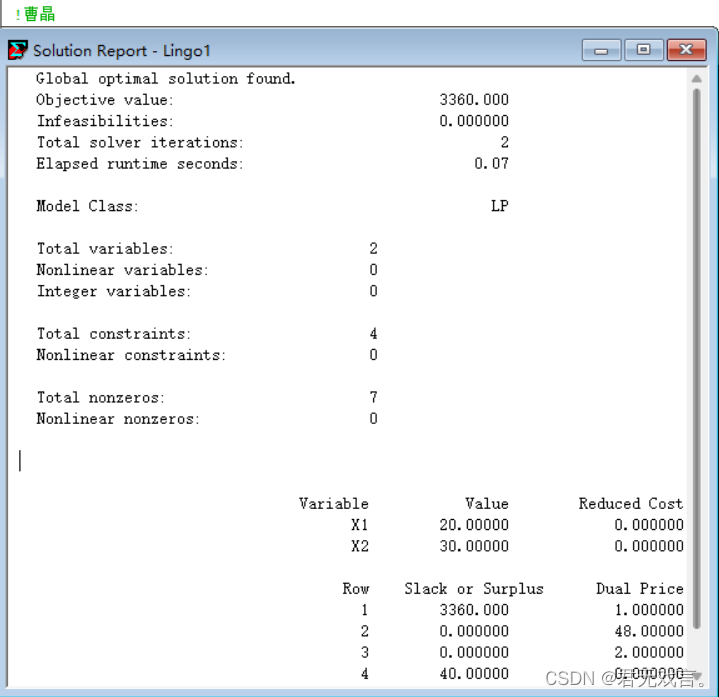
程序代码: MODEL: MAX=72*x1+64*x2; x1+x2<50; 12*x1+8*x2<480; 3*x1<100; END 程序执行结果:
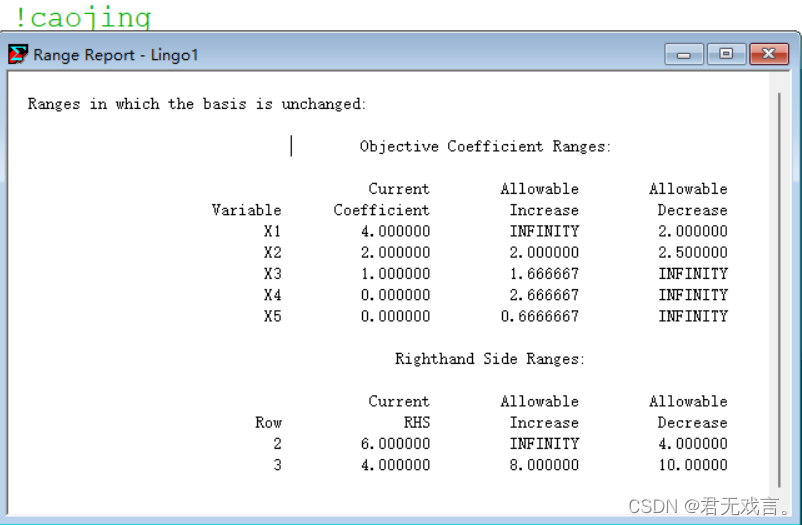
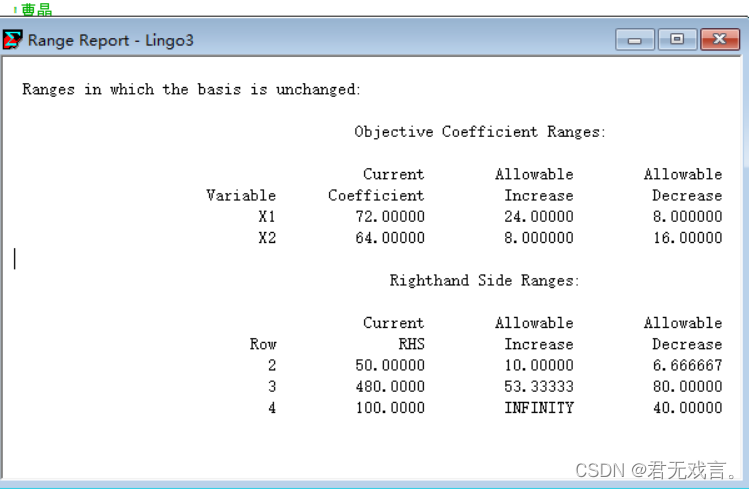
结果解释: X1,x2分别为20、3桶时,可使得利润达到最大,最大利润为3360元; reduced cost结果解释: 变量x1对应的reduced cost值为-72,表示x1减少一桶时,利润减少72元。同理,x2减少一桶时,利润减少64元。 Slack or Surplus结果解释: Slack or Surplus值为给出的松驰变量值,可以看出每天供应牛奶桶数和每天工人总的劳动时间都达到了上限,低于甲车间加工能力上限40公斤。 Dual price结果解释: 1.增加每天供应牛奶桶数1单位可利润增加48元, 2.增加每天工人总的劳动时间1单位可利润增加2元。 35<48由此可见 ,若用35元可以买到1桶牛奶,应作这项投资。(第一个问题答案) 由于增加1个小时总劳动时间利润仅增加2元,所以最多付给工人每小时两元。(第二个问题答案) 目标函数系数和约束条件右端常数项的灵敏度分析: Objective Coefficient Ranges(系数价格变化)结果分析: 对于x1来说,目标函数中原来的系数为72,允许增加(Allowable Increase)24、或者允许减少(Allowable Decrease)8,说明当它在[72-8,72+24]=[ 64,96]范围变化时,最优基保持不变。同理,对于x2来说,目标函数中原来的系数为64,允许增加(Allowable Increase)8、或者允许减少(Allowable Decrease)16,说明当它在[64-16,64+8]=[ 48,72]范围变化时,最优基保持不变。 又由每公斤A1获利30元,则用一桶牛奶生产x1获利90元,即x1系数为90,在[64,96] 区间内,所以不需要改变生产计划。(第三个问题答案) Right hand Side Ranges (约束中右端项变化)结果分析: 每天供应牛奶桶数(桶数为整数)在区间[43.33333,60]内,每天工人总的劳动时间在区间[400,533.33333]内时,最优基保持不变。(由于目标函数中费用系数发生了变化,所以最优值会变化)。所以此时投资牛奶最多购买60-50=10桶牛奶(第一个问题答案)。 | ||||||||
| 分析与讨论:
“Reduced Cost”表示当变量有微小变动时, 目标函数的变化率。其中基变量的reduced cost值应为0,对于非基变量 Xj, 相应的 reduced cost值表示当某个变量Xj 增加一个单位时目标函数增加的量。例如变量x1对应的reduced cost值为3,表示当非基变量x1的值从0变为 1时(此时假定其他非基变量保持不变),最优目标值为 z= 18.66667+3 = 21.66667。
“Slack or Surplus”给出松驰变量的值:例如题目5Slack or Surplus值为给出的松驰变量值,可以看出每天供应牛奶桶数和每天工人总的劳动时间都达到了上限,低于甲车间加工能力上限40公斤。
Dual Price(对偶价格)表示当对应约束有微小变动时, 目标函数的变化率。输出结果中对应于每一个约束有一个对偶价格。 若其数值为p, 表示对应约束中不等式右端项若增加1 个单位,目标函数将增加p个单位(max型问题)。
对于x1来说,目标函数中原来的系数为72,允许增加(Allowable Increase)24、或者允许减少(Allowable Decrease)8,说明当它在[72-8,72+24]=[ 64,96]范围变化时,最优基保持不变。同理,对于x2来说,目标函数中原来的系数为64,允许增加(Allowable Increase)8、或者允许减少(Allowable Decrease)16,说明当它在[64-16,64+8]=[ 48,72]范围变化时,最优基保持不变。
虽然限制量在最终得到的一个区间里变化,最优基保持不变,但由于此时约束没有变化(只是目标函数中某个费用系数发生变化),所以最优基保持不变的意思也就是最优解不变。并且由于目标函数中费用系数发生了变化,所以最优值会变化。 |
最优化系列 之 线性规划问题的灵敏度分析(1/6)
news2026/2/13 2:26:43
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如若转载,请注明出处:http://www.coloradmin.cn/o/679070.html
如若内容造成侵权/违法违规/事实不符,请联系多彩编程网进行投诉反馈,一经查实,立即删除!相关文章
【spring cloud学习】2、Eureka服务注册与发现
前言
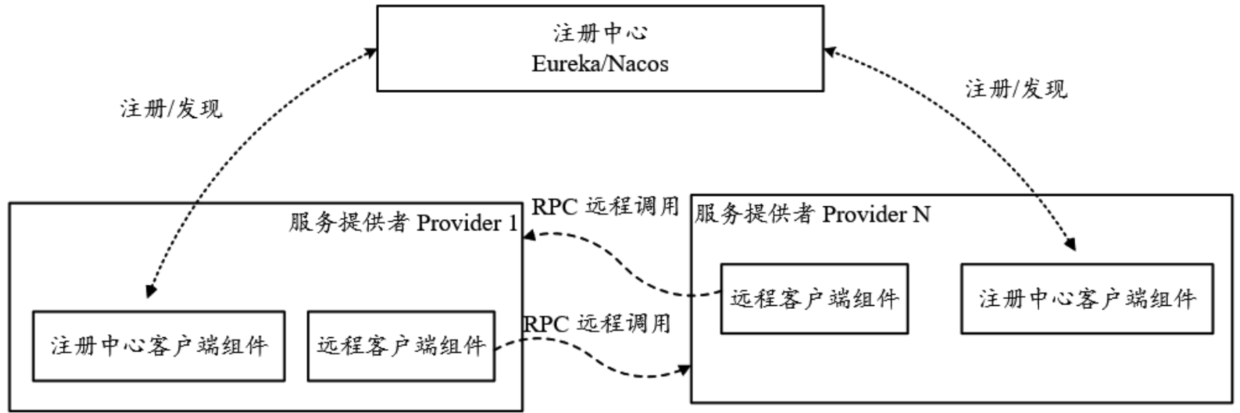
一套微服务架构的系统由很多单一职责的服务单元组成,而每个服务单元又有众多运行实例。由于各服务单元颗粒度较小、数量众多,相互之间呈现网状依赖关系,因此需要服务注册中心来统一管理微服务实例,维护各服务实例的健康状态…
Linux用户信息关键文件详解
passwd文件说明
/etc/passwd文件记录了Linux所有用户的信息,是系统的关键文件之一。 文件格式内容如上图。
文件中的条目以“:”为分隔符,各个字段记录的信息依次为:
第一个字段:记录用户名
第二个字段:值x表示该用…
如何做一份干净的git提交记录
背景
毕业工作有一些年头了,之前在写工作代码或者给开源项目贡献的时候,提交代码都不是很规范,甚至可以说十分的随意,想到什么就提交什么,根本没有管理提交记录的概念或者想法(当你身边的人都不怎么在意的…
基于SpringBoot+SpringCloud+vue的智慧养老平台设计与实现
博主介绍: 大家好,我是一名在Java圈混迹十余年的程序员,精通Java编程语言,同时也熟练掌握微信小程序、Python和Android等技术,能够为大家提供全方位的技术支持和交流。 我擅长在JavaWeb、SSH、SSM、SpringBoot等框架…
大数据企业开发全套流程
大数据企业开发基础流程
Linux命令
1 Hadoop(HDFSYarn)单机版环境搭建 Hadoop 是一个开源的分布式计算框架,由 HDFS(Hadoop Distributed File System)和 YARN(Yet Another Resource Negotiator)两个核心组件组成。HD…
网络安全的含义及特征
网络安全从其本质上讲就是网络上的信息安全,指网络系统的硬件、软件及数据受到保护。不遭受破坏、更改、泄露,系统可靠正常地运行,网络服务不中断。从用户的角度,他们希望涉及到个人和商业的信息在网络上传输时受到机密性、完整性…
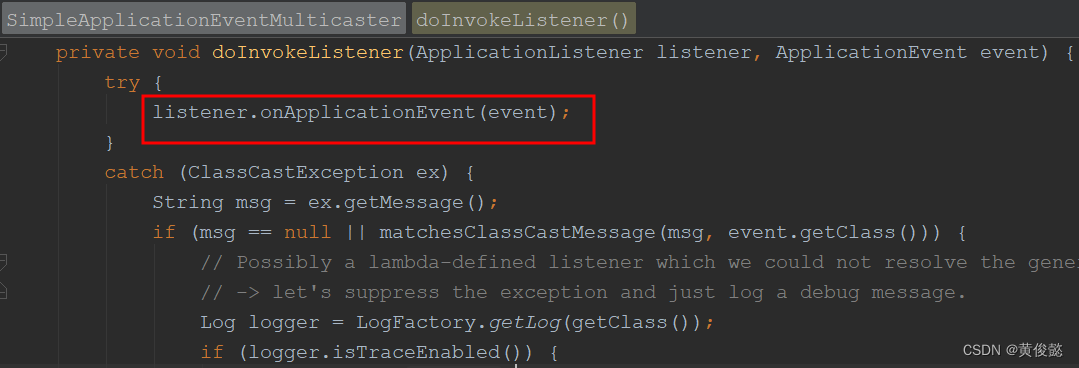
人人都能看懂的Spring源码解析,spring的事件监听机制
人人都能看懂的Spring源码解析,spring的事件监听机制 原理解析事件监听机制ApplicationEventPublisher、ApplicationEventMulticaster、ApplicationEvent、ApplicationListenerAbstractApplicationContext发布的事件类型 代码走读总结 往期文章:
人人都…
大数据Doris(四十八):Steam Load案例和注意事项
文章目录
Steam Load案例和注意事项
一、Steam Load案例
1、准备数据
2、创建 Doris 表
3、创建 Stream Load 导入任务
4、查看任务
5、查询Doris 表结果
二、注意事项 Steam Load案例和注意事项
一、Steam Load案例
下面以导入Linux节点本地磁盘数据到Doris为例&…
Python小游戏集合(开源、开源、免费下载)
Python小游戏集合 0. 前言1. 为什么用Python做游戏2. 小游戏集合及源代码(整理不易,一键三连)2.1 外星人小游戏2.2 塔防小游戏2.3 三国小游戏2.4 打飞机游戏2.5 飞机大战小游戏2.6 玛丽快跑小游戏2.7 涂鸦跳跃小游戏2.8 猜数字小游戏2.9 坦克…
金蝶云星空财务账套数据库中了.locked勒索病毒的解密步骤和预防方式
最近,金蝶云星空财务账套的数据库遭到了一次严重的勒索病毒攻击,导致数据库中重要数据被加密。这种攻击对企业来说是一种巨大的威胁,因为数据是企业的核心资产之一。而此次攻击的病毒为.locked后缀勒索病毒,而locked勒索病毒在本月…
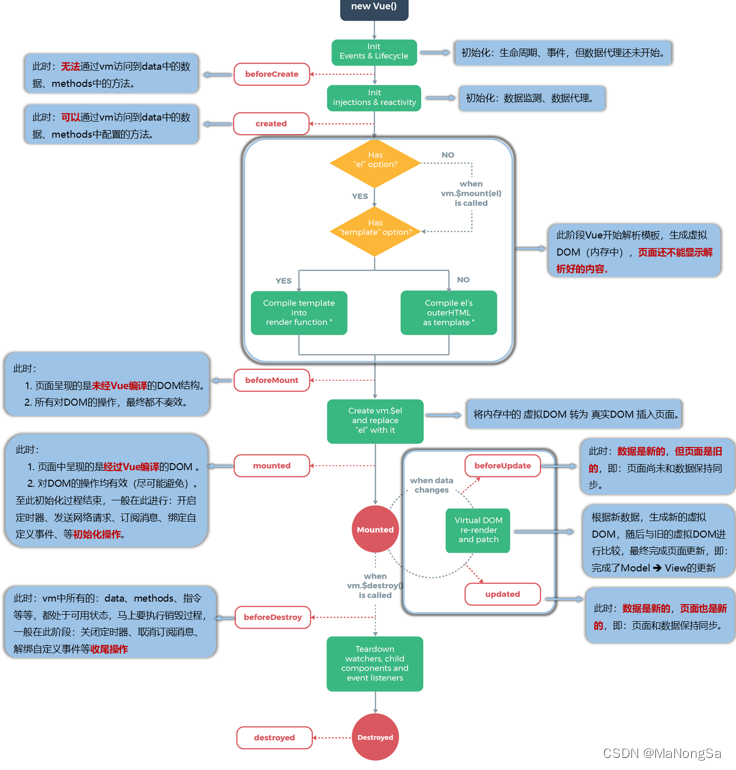
VUE L 生命周期 ⑩①
目录 文章有误请指正,如果觉得对你有用,请点三连一波,蟹蟹支持✨ V u e j s Vuejs Vuejs初见生面周期分析生命周期生命周期总结总结 文章有误请指正,如果觉得对你有用,请点三连一波,蟹蟹支持✨ ⡖⠒⠒⠒⠤⢄…
Spring 项目过程及如何使用 Spring
文章目录 1.创建 Spring 项目步骤1.1 创建 Maven 项目1.2添加 Spring 框架支持1.3 添加启动项2.如何使用 Spring2.1 存储 Bean 对象2.1.1 创建 Bean对象2.1.2 将 Bean对象注册到容器中 2.2 获取并使用 Bean对象2.2.1 使用 ApplicationContext 获取对象2.2.2 使用 BeanFactory 获…
五、Docker镜像发布到阿里云/私有库
学习参考:尚硅谷Docker实战教程、Docker官网、其他优秀博客(参考过的在文章最后列出) 目录 前言一、本地镜像发布到阿里云1.1 流程图1.2 注册阿里云创建容器服务个人实例1.3 创建命名空间1.4 创建镜像仓库1.5 将镜像推送到阿里云本地仓库 二、从阿里云仓库拉去自己推…
Matlab统计分析 -- 聚类算法模型
统计分析 – 聚类算法模型
距离分析 数据标准化
欧氏距离与量纲有关,因此,有时需要对数据进行预处理, 如标准化等。 在MATLAB中的命令是zscore,调用格式
Z zscore(X)
输入X表示N行p列的原始观测矩阵,行为个体&…
Nginx-反向代理详解
本文已收录于专栏 《中间件合集》 目录 概念说明什么是Nginx什么是反向代理 功能介绍配置过程1.修改nginx配置文件修改全局模块修改工作模块修改HTTP模块 2.保存配置文件3.重启配置文件4.查看配置文件是否重启成功 配置反向代理的好处总结提升 概念说明
什么是Nginx Nginx 是一…
你真的会写 HelloWorld 吗?
目录
Hello World
写一个批处理命令行脚本
关于include
关于程序的入口
输出充定向
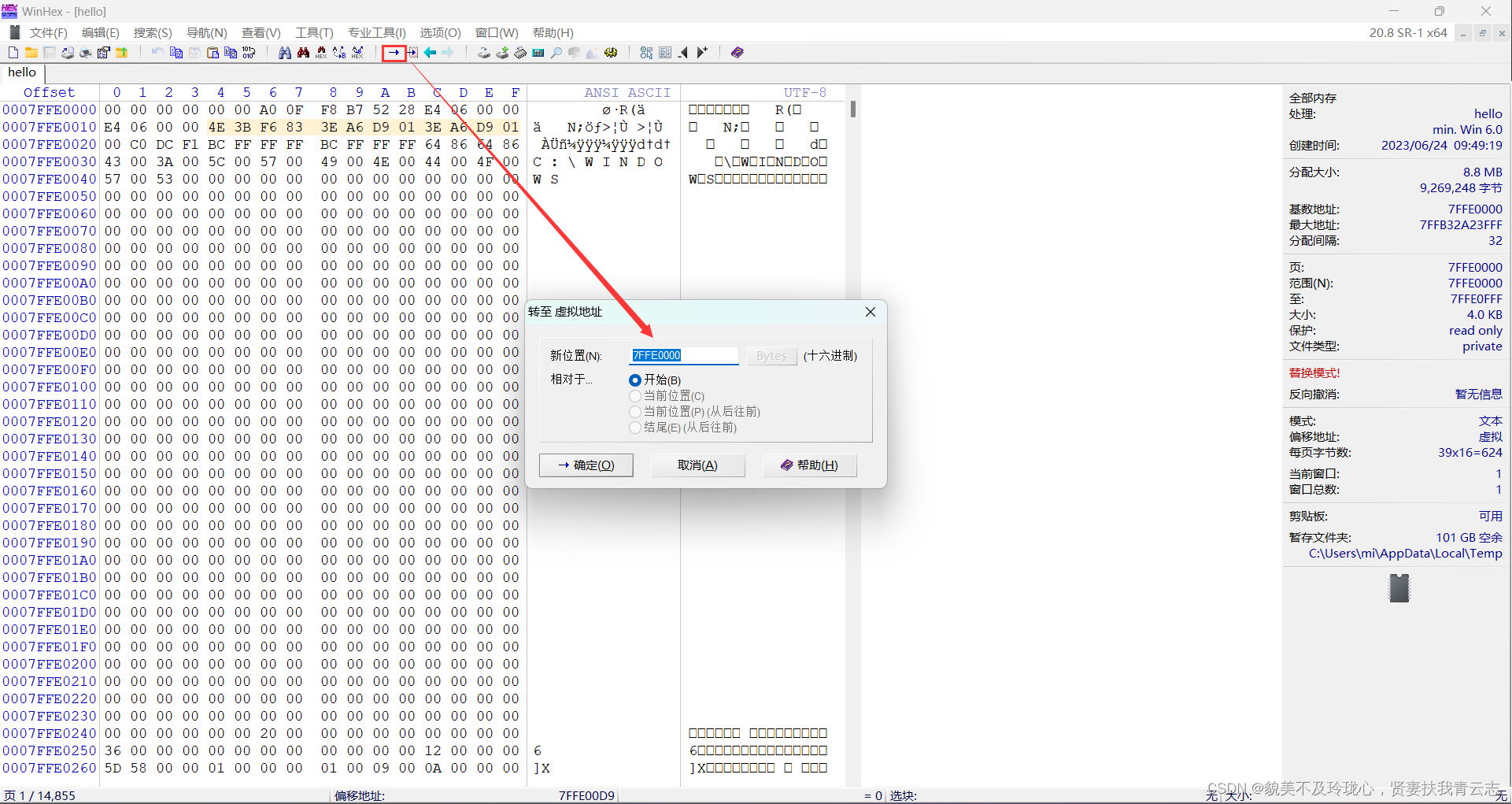
在内存的存储详情
WinHex工具介绍 初学C语言时,第一个程序一定是Hello World!。但是Hello World的具体实现细节你真的了解吗? Hello World
C语言代码如下&#…
SSM国内热门景点推荐系统的开发-计算机毕设 附源码83762
SSM国内热门景点推荐系统的开发 摘 要 为了方便用户快速定位自己感兴趣的国内热门旅游景点信息,国内热门景点推荐系统应运而生。本系统的前端界面主要实现页面的美观和动态效果使之符合广大群众的审美观,后台主要使用的技术主要有Java编程语言࿰…
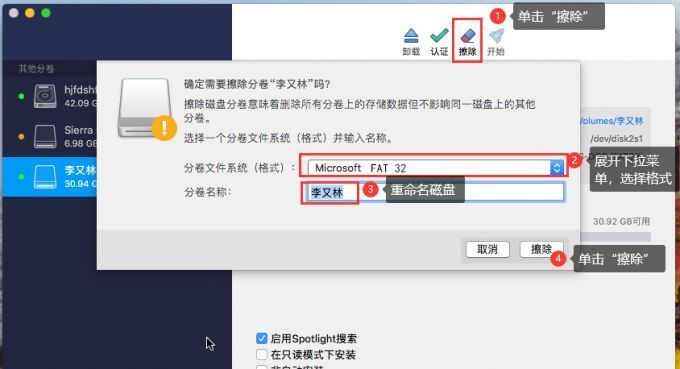
Paragon NTFS2023Mac读取、写入外置移动硬盘软件
在我们日常使用电脑时常常会出现NTFS格式分区,那你知道NTFS For Mac是什么?简单的理解就是让你在mac系统下,可以正常读写Windows的Ntfs格式的分区。其中还包括Windows NT 4,2000,XP,2003,Vista&…
springboot 新农村信息化管理与服务平台-计算机毕设 附源码83372
springboot 新农村信息化管理与服务平台 目 录 摘要 1 绪论 1.1新农村信息化概念 1.2研究内容 1.3springboot框架介绍 1.4论文结构与章节安排 2 新农村信息化管理与服务平台系统分析 2.1 可行性分析 2.1.1 技术可行性分析 2.1.2 经济可行性分析 2.1.3 法律可行性分析…