一.线索二叉树的结点结构:
| lchild | ltag | data | rtag | rchild |
ltag = 0, lchild域指示结点的左孩子
ltag = 1, lchild域指示结点的前驱
rtag = 0, rchild域指示结点的右孩子
rtag = 1, rchild域指示结点的后继
这里用char型作为树的数据域类型
//定义线索二叉树的结构体
typedef struct ThreadNode
{
char data;
struct ThreadNode *lchild,*rchild;
int ltag,rtag;
}ThreadNode,*ThreadTree;二.如何找寻结点的前驱和后继
先将二叉树进行遍历然后根据遍历结构来找前驱和后继
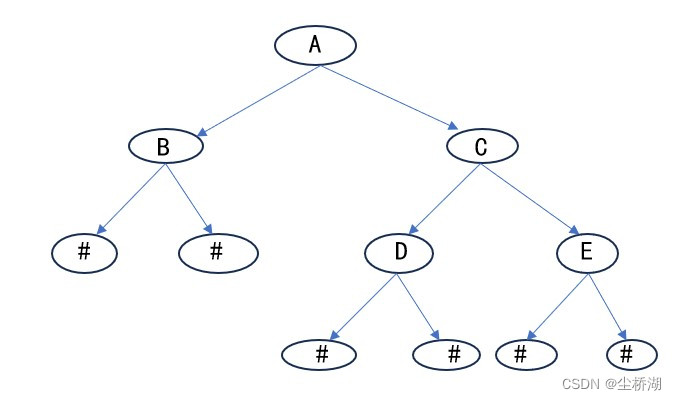
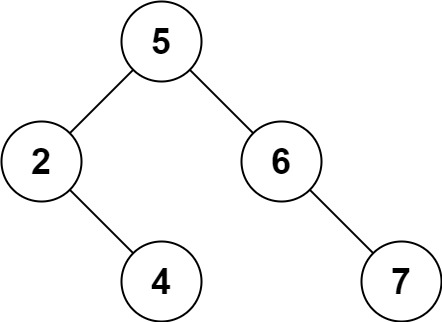
以该例子的中序来表示,该二叉树的中序遍历为:BADCE
B的前驱结点为NULL,后继结点为A
A的前驱结点为B,后继结点为D
D的前驱结点为A,后继结点为C
C的前驱结点为D,后继结点为E
E的前驱节点为C,后继结点为NULL
由上图可以看出有的结点的指针域是空的,这样可以利用这些空的指针域,若左孩子指针域为空可以指向该结点的前驱结点;若右孩子为空,可以指向该结点的后继结点

红色线表示前驱指向前驱结点,黄色线表示指向后继结点
三.二叉树线索化过程
1.先通过字符串为二叉树赋值
字符串结构体
//定义字符串的结构体
typedef struct SString
{
char ch[Maxsize];
int length;
}SString;
串赋值操作
//串的赋值操作
void StrAssign(SString &S, char *chars)
{
if(strlen(chars) > Maxsize)
exit(-1);
S.length = strlen(chars);
S.ch[0] = S.length;
for(int i = 1; i <= S.length; ++i )
{
S.ch[i] = *(chars+i-1);
}
}构造二叉树
//先创造一棵树,将chars元素赋值给树
void CreatTree(ThreadTree &T)
{
char ch = S.ch[i++];
if(ch == '#')
T = NULL;
else
{
T = (ThreadTree)malloc(sizeof(ThreadNode));
if(T == NULL)
{
printf("动态内存分配失败,结束程序!\n");
exit(-1);
}
T->data = ch;
CreatTree(T->lchild);
if(T->lchild != NULL)
T->ltag = 0;
CreatTree(T->rchild);
if(T->rchild != NULL)
T->rtag = 0;
}
}
2.中序遍历线索二叉树
//中序遍历二叉树,一边遍历一边线索化
void InThread(ThreadTree &T)
{
if(T != NULL)
{
InThread(T->lchild);//中序遍历左子树
Visit(T);//访问结点
InThread(T->rchild);//中序遍历右子树
}
}访问结点函数
//访问节点
void Visit(ThreadNode *p)
{
if(p->lchild == NULL)//如果左子树为空,建立前驱线索
{
p->lchild = Pre;
p->ltag = 1;
}
if(Pre != NULL && p->rchild == NULL)//建立后继线索
{
p->rchild = Pre;
p->rtag = 1;
}
Pre = p;
}中序线索化二叉树
//中序线索化二叉树
void CreatInThread(ThreadTree &T)
{
Pre = NULL;//初始时Pre为NULL
if(T != NULL)//非空二叉树才能够线索化
{
InThread(T);//中序线索化
if(Pre->rchild == NULL)
Pre->rtag = 1;//处理遍历的最后一个结点
}
}3.找前驱结点
首先是找到以P为根结点的的子树中,最后一个被中序遍历的结点
//中序线索二叉树找中序前驱,线索二叉树中序遍历中,以P为根结点,则P的前驱肯定是在P的左子树中最右下结点
//找到以P为根结点的的子树中,最后一个被中序遍历的结点
ThreadNode *LastNode(ThreadNode *P)
{
while(P->rtag == 0)
P = P->rchild;
return P;
}左子树最右下结点
//在中序线索二叉树中找到结点P的前驱结点
ThreadNode *Prenode(ThreadNode *P)
{//左子树中最右下结点
if(P->ltag == 0)
return LastNode(P->lchild);
else
return P->lchild;
}4.找后继结点
找左子树最左下结点
//中序线索二叉树找中序后继,在中序线索二叉树中,若是找根结点的后继节点,那么肯定是右子树中第一个遍历的结点
//右子树的最左下结点
ThreadNode *firstnode(ThreadNode *P)
{
while(P->ltag == 0)
P = P->lchild;
return P;
}
右子树最左下结点
//在中序遍历的线索二叉树中,以P为根节点,找P结点的中序遍历后继结点
ThreadNode *nextnode(ThreadNode *P)
{//右子树最左下结点
if(P->rtag == 0)
return firstnode(P->rchild);
else
return P->rchild;
}
结果

5.二叉树先序遍历线索化
//先序遍历线索化,一边遍历一边线索化
void PreThread(ThreadTree T)
{
if(T != NULL)
{
Visit(T);//先访问根结点
if(T->ltag == 0)//防止因为线索而导致一直循环
PreThread(T->lchild);//访问左子树
PreThread(T->rchild);//访问右子树
}
}
//创造先序线索化二叉树
void CreatPreThread(ThreadTree T)
{
Pre = NULL;
if(T != NULL)
{
PreThread(T);
if(Pre->rchild == NULL)
Pre->rtag = 1;//处理最后一个结点
}
}完整代码
#include<stdio.h>
#include<stdlib.h>
#include<malloc.h>
#include<string.h>
#define Maxsize 11
//定义线索二叉树的结构体
typedef struct ThreadNode
{
char data;
struct ThreadNode *lchild,*rchild;
int ltag,rtag;
}ThreadNode,*ThreadTree;
//定义一个全局变量
ThreadNode *Pre = NULL;
//定义字符串的结构体
typedef struct SString
{
char ch[Maxsize];
int length;
}SString;
//定义一个全局变量的字符串
SString S;
int i = 1;
//串的函数说明
void StrAssign(SString &S, char *chars);
//树的函数说明
void CreatTree(ThreadTree &T);
void InThread(ThreadTree &T);
void Visit(ThreadNode *p);
void CreatInThread(ThreadTree &T);
ThreadNode *LastNode(ThreadNode *P);
ThreadNode *Prenode(ThreadNode *P);
ThreadNode *firstnode(ThreadNode *P);
ThreadNode *nextnode(ThreadNode *P);
int main(void)
{
ThreadTree T;
StrAssign(S,"AB##CD##E##");
CreatTree(T);
ThreadNode *V1 = Prenode(T);
ThreadNode *V2 = nextnode(T);
printf("根结点的前驱结点的值为:%c\n",V1->data);
printf("根结点的后继结点的值为:%c\n",V2->data);
return 0;
}
//串的赋值操作
void StrAssign(SString &S, char *chars)
{
if(strlen(chars) > Maxsize)
exit(-1);
S.length = strlen(chars);
S.ch[0] = S.length;
for(int i = 1; i <= S.length; ++i )
{
S.ch[i] = *(chars+i-1);
}
}
//先创造一棵树,将chars元素赋值给树
void CreatTree(ThreadTree &T)
{
char ch = S.ch[i++];
if(ch == '#')
T = NULL;
else
{
T = (ThreadTree)malloc(sizeof(ThreadNode));
if(T == NULL)
{
printf("动态内存分配失败,结束程序!\n");
exit(-1);
}
T->data = ch;
CreatTree(T->lchild);
if(T->lchild != NULL)
T->ltag = 0;
CreatTree(T->rchild);
if(T->rchild != NULL)
T->rtag = 0;
}
}
//中序遍历二叉树,一边遍历一边线索化
void InThread(ThreadTree &T)
{
if(T != NULL)
{
InThread(T->lchild);//中序遍历左子树
Visit(T);//访问结点
InThread(T->rchild);//中序遍历右子树
}
}
//访问节点
void Visit(ThreadNode *p)
{
if(p->lchild == NULL)//如果左子树为空,建立前驱线索
{
p->lchild = Pre;
p->ltag = 1;
}
if(Pre != NULL && p->rchild == NULL)//建立后继线索
{
p->rchild = Pre;
p->rtag = 1;
}
Pre = p;
}
//中序线索化二叉树
void CreatInThread(ThreadTree &T)
{
Pre = NULL;//初始时Pre为NULL
if(T != NULL)//非空二叉树才能够线索化
{
InThread(T);//中序线索化
if(Pre->rchild == NULL)
Pre->rtag = 1;//处理遍历的最后一个结点
}
}
//中序线索二叉树找中序前驱,线索二叉树中序遍历中,以P为根结点,则P的前驱肯定是在P的左子树中最右下结点
//找到以P为根结点的的子树中,最后一个被中序遍历的结点
ThreadNode *LastNode(ThreadNode *P)
{
while(P->rtag == 0)
P = P->rchild;
return P;
}
//在中序线索二叉树中找到结点P的前驱结点
ThreadNode *Prenode(ThreadNode *P)
{//左子树中最右下结点
if(P->ltag == 0)
return LastNode(P->lchild);
else
return P->lchild;
}
//中序线索二叉树找中序后继,在中序线索二叉树中,若是找根结点的后继节点,那么肯定是右子树中第一个遍历的结点
//右子树的最左下结点
ThreadNode *firstnode(ThreadNode *P)
{
while(P->ltag == 0)
P = P->lchild;
return P;
}
//在中序遍历的线索二叉树中,以P为根节点,找P结点的中序遍历后继结点
ThreadNode *nextnode(ThreadNode *P)
{//右子树最左下结点
if(P->rtag == 0)
return firstnode(P->rchild);
else
return P->rchild;
}
//先序遍历线索化,一边遍历一边线索化
void PreThread(ThreadTree T)
{
if(T != NULL)
{
Visit(T);//先访问根结点
if(T->ltag == 0)//防止因为线索而导致一直循环
PreThread(T->lchild);//访问左子树
PreThread(T->rchild);//访问右子树
}
}
//创造先序线索化二叉树
void CreatPreThread(ThreadTree T)
{
Pre = NULL;
if(T != NULL)
{
PreThread(T);
if(Pre->rchild == NULL)
Pre->rtag = 1;//处理最后一个结点
}
}