一、说明

        PageRank是经典的网页热度评分算法，在自然语言的热词提取也有同样的意义（TextRank）；本文详细叙述该算法的原理，配合部分代码演示其原理。        

二、PageRank算法的启发因素

2.1 算法兴起

        PageRank (PR) 是 Google 搜索使用的一种算法，用于在其搜索引擎结果中对网页进行排名。1996 年由Page和Brin提出，它以“网页”一词和联合创始人拉里佩奇的名字命名。 PageRank 是一种衡量网站页面重要性的方法。这个算法后被NLP采用，作为词热度的算法如TextRank,本篇专门研究这个算法。

        PageRank 可以定义在任意有向图上，而与之类似的问题都可以用此模型，因而被应用到社会影响力分析、文本摘要等多个问题，成了越来越被关注的经典算法。

2.2 算法的理论依据

        PageRank算法的基本想法是在有向图上定义一个随机游走模型，即一阶马尔可夫链，描述随机游走者沿着有向图随机访问各个结点的行为。在一定条件下，极限情况访问每个结点的概率收敛到平稳分布，这时各个结点的平稳概率值就是其PageRank值，表示结点的重要度。PageRank 是递归定义的，PageRank 的计算可以通过迭代算法进行。

2.3 关于网页热度的假设

        网页的热度究竟如何定义才算好？其实很朴素的理由决定了一个大的作d为。

        历史上，PageRank算法作为计算互联网网页重要度的算法被提出。PageRank是定义在网页集合上的一个函数，它对每个网页给出一个正实数，表示网页的重要程度，整体构成一个向量，PageRank值越高，网页就越重要，在互联网搜索的排序中可能就被排在前面。

        也就是大白话：

•         人家访问我，给我增加热度，人家热度不变；
•         我访问人家，给人家增加热度。我的热度不变

2.4 有向图的崛起

        AI研究者应该对有向图敏感起来，对于许多类网络模型，实际上都有意义。

        在实际应用中许多数据都以图（graph）的形式存在，比如，互联网、社交网络都可以看作是一个图。图数据上的机器学习具有理论与应用上的重要意义。 PageRank 算 法是图的链接分析（link analysis）的代表性算法，属于图数据上的无监督学习方法。

三、PageRank算法描述

        设计本算法用到的概念是：有向图、节点出度和入度、转移矩阵、递归；

        算法：下面是实现随机漫步方法的步骤。

• 创建一个具有N个节点的有向图。
• 现在进行随机漫步。
• 现在，在随机行走过程中根据点对节点进行排序。
• 最后，将其与内置的PageRank方法进行了比较。

3.1 构建一个网络有向图

        假如一个局域网的网络环境，随着业务进行，有如下访问网络有向图。 网络可以像有向图一样表示，其中节点表示网页，边在它们之间形成链接。通常，如果节点（网页）i链接到节点j，则意味着i指的是j。

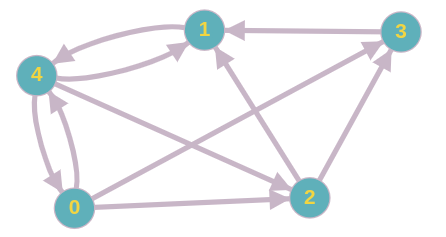
 3.2 知名度模型

        我们必须定义什么是网页的重要性。作为第一种方法，我们可以说是指引用它的网页的总数。如果我们停止使用这个标准，那么引用它的这些网页的重要性就不会被考虑在内。换句话说，一个重要的网页和一个不太重要的网页具有相同的权重。另一种方法是假设一个网页将其重要性平均分配给它链接到的所有网页。通过这样做，我们可以定义节点j的分数如下：、

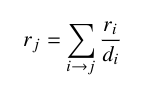
        其中rᵢ是节点i和的分数，dᵢ是i节点的出度。Σ是所有节点i，其中对j节点有出度，我们可以写出这个线性系统：

        通过把这个线性系统的右边代入左边，我们得到了一个新的线性系统，我们可以用高斯消去法求解。但这种解决方案仅限于小型图。事实上，由于这类图是稀疏的，并且高斯消去法在执行其运算时会修改矩阵，因此我们会失去矩阵的稀疏性，并占用更多的内存空间。在最坏的情况下，不能再存储矩阵。

 3.3 构成一维马尔可夫链和（Markov Chain）

        由于马尔可夫链是由初始分布和转移矩阵定义的，因此上图可以被视为具有以下转移矩阵的马尔可夫链：

        与我们的示例相对应的转换矩阵，我们注意到P转置是行随机的，这是应用马尔可夫链定理的一个条件。对于初始分布，让我们考虑它等于：

        其中n是节点的总数。这意味着随机行走器将随机选择它可以到达所有其他节点的初始节点。

        在每一步，随机行者都会根据转移矩阵跳到另一个节点。然后计算每个步骤的概率分布。这个分布告诉我们，经过一定数量的步骤后，随机游走者可能会在哪里。概率分布使用以下公式计算：

        马尔可夫链的平稳分布是π=Pπ的概率分布π。这意味着一步之后分布不会改变。需要注意的是，并不是所有的马尔可夫链都允许平稳分布。

        如果马尔可夫链是强连通的，这意味着任何节点都可以从任何其他节点到达，那么它允许平稳分布。我们的问题就是这样。因此，经过无限长的步行，我们知道概率分布将收敛到平稳分布π。

3.4 计算方法

        （以上我们已经清楚知道这个模型的设计方法，其它就是个算法问题了） 

        我们注意到π是特征值为1的矩阵P的特征向量。我们使用Frobenius-Perron定理，而不是计算P的所有特征向量并选择对应于特征值1的特征向量。

        根据Frobenius-Perron定理，如果矩阵a是一个平方正矩阵（它的所有项都是正的），则它有一个正的特征值r，如|λ|<r，其中λ是a的特征值。具有特征值r的A的特征向量v是正的，并且是唯一的正特征向量。

        在我们的例子中，矩阵P是正的和平方的。平稳分布π必然是正的，因为它是一个概率分布。我们得出π是P的主特征向量，其主特征值为1。

        为了计算π，我们使用幂法迭代，这是一种计算给定矩阵a的主特征向量的迭代方法。从可以随机初始化的主特征向量b的初始近似开始，该算法将使用以下算法更新它直到收敛：

四、实验代码

1）对一个具体图的迭代算法。此为原理性伪代码。

2）更正规的代码，对任意有向图进行迭代收敛：见本文title的上传资源（80行python）。