上节说到了相机模型,那么这节说说相机的畸变
如果有手机爱好者,听到很多测评进行测评的时候,都会提到一个词,广角防畸变,啥意思,举个栗子
来看下信号塔,是不是已经开始歪了,这就是0.6倍,超广角模式下的畸变(其实一倍也畸变,小声BB)
为啥会畸变呢,仔细看镜头,镜头是曲面的,光从镜头射入的时候和射入平面玻璃的时候,路径是不一样的,玩过放大镜和哈哈镜的都有印象吧.
小时候拿些放大镜对着太阳烧东西,你烧通老爹的几次裤衩,又挨了老爹多少次的暴打.
所以畸变不可避免,但是可以后期修补.
镜头的畸变分为径向畸变和切向畸变两类
径向畸变
由透镜的形状引起的畸变称为径向畸变
曲率大的(比较圆)镜头比曲率小的(比较平)镜头畸变大(我喜欢圆的,嘿嘿嘿)
咳咳(严肃脸),这个是因为构造导致的,无法避免
径向畸变分为枕形畸变和桶形畸变
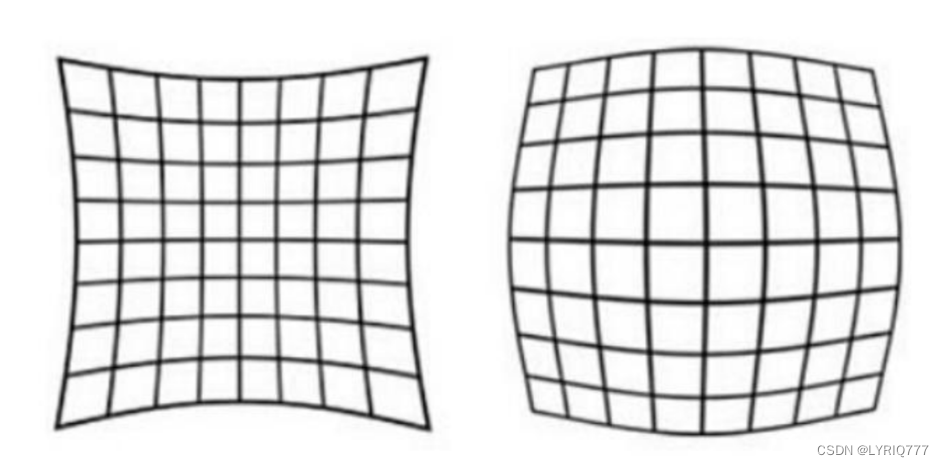
左图为枕形畸变(凹面),右图为桶形畸变(凸面)
切向畸变
切向畸变是由于透镜本身与相机传感器平面(成像平面)或图像平面不平行而产生的.这种情况多是由于透镜被粘贴到镜头模组上的安装偏差导致.
这种纯是品控问题,这里点名某国内粗粮厂,品控极差!
畸变矫正

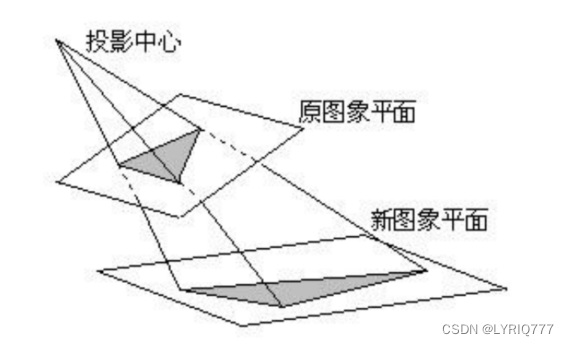
透视变换(Perspective Transformation)
透视变换是将图片投影到一个新的视平面(Viewing Plane),也称作投影映射(Projective Mapping)。
我们常说的仿射变换是透视变换的一个特例。
透视变换的目的就是把现实中为直线的物体,在图片上可能呈现为斜线,通过透视变换转换成直线的变换。
仿射变换(Affine Transformation或 Affine Map),又称为仿射映射,是指在几何中,图像进行从一个向量空间进行一次线性变换和一次平移(有没有很熟悉),变换为到另一个向量空间的过程。
怎么做?
找四个对应点的坐标
A(x1y1)→A1(x11,y11)
B(x2,y2)→B1(x21,y21)
C(x3,y3)→C1(x31,y31)
D(x4,y4)→D1(x41,y41)
然后计算出一个对应关系,然后依照该对应关系进行全图变换






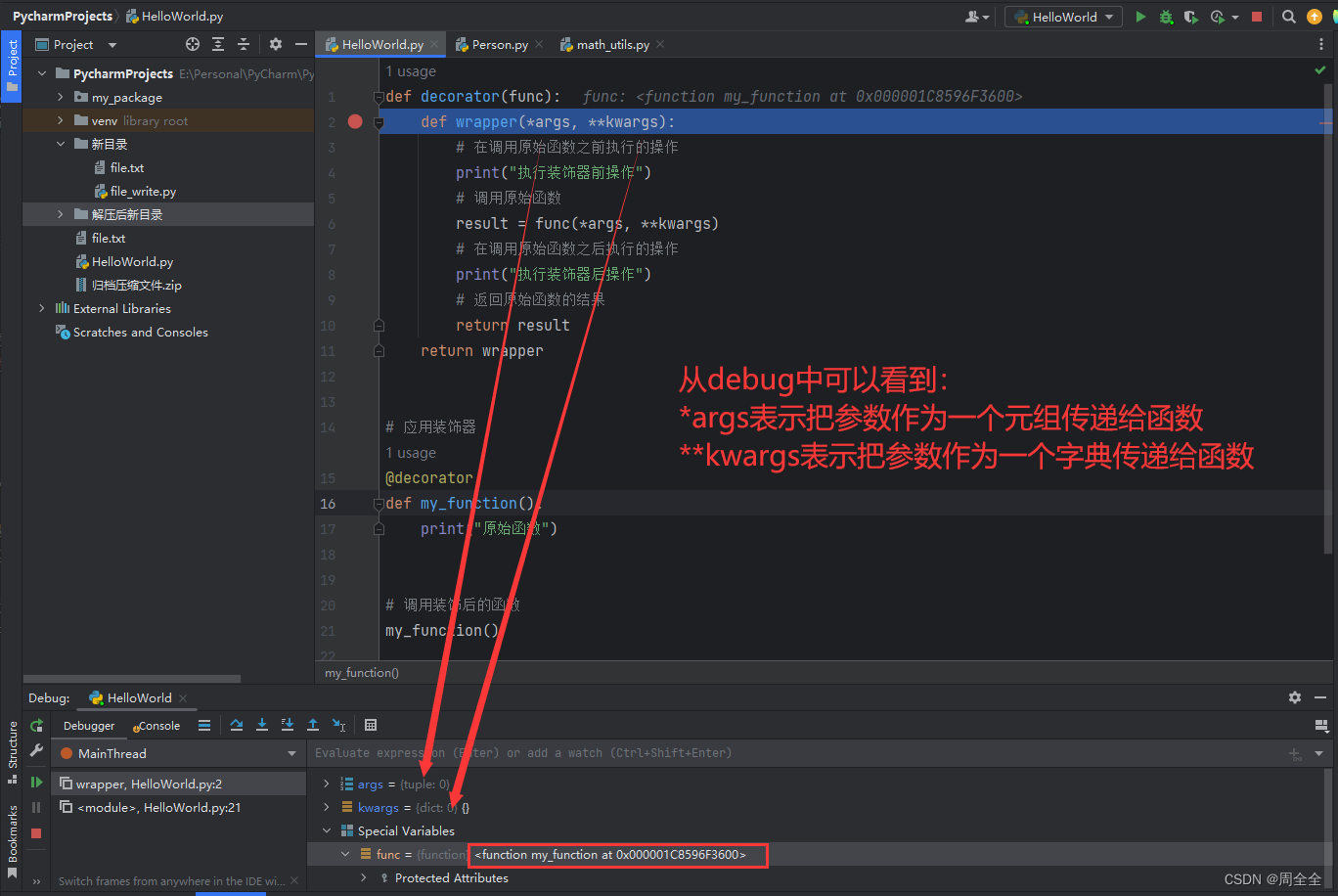
![[英语单词] gated; cycle gated](https://img-blog.csdnimg.cn/63e58cf028754107bb7984e2717c8228.png#pic_center)