PID控制算法 – 0、PID原理

news2024/11/15 9:17:54

1、开局一张图

很多地方都觉得PID的控制结构示意图是这样的：

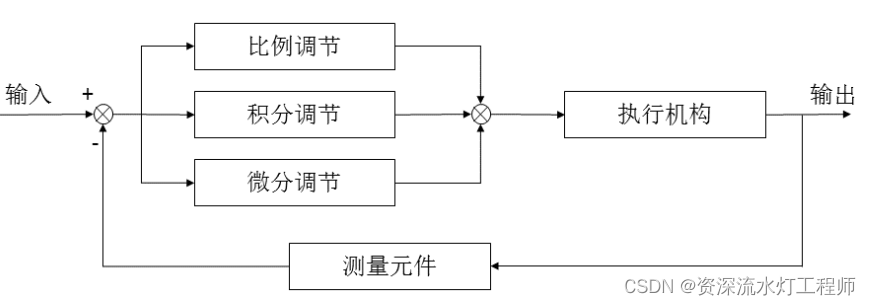
2、目标值（Setpoint）、输入值（Input）、误差（Error）

其实把上图那个输入改为目标值（Setpoint）更合适，因为不管是什么控制系统，都应该有个目标值，比如水位控制系统，水位的高度就是目标值；温度控制系统，想要的温度就是目标值；速度控制系统，想要的速度就是目标值。目标值是所有控制系统的前提，所以PID控制结构示意图应该改为这样：

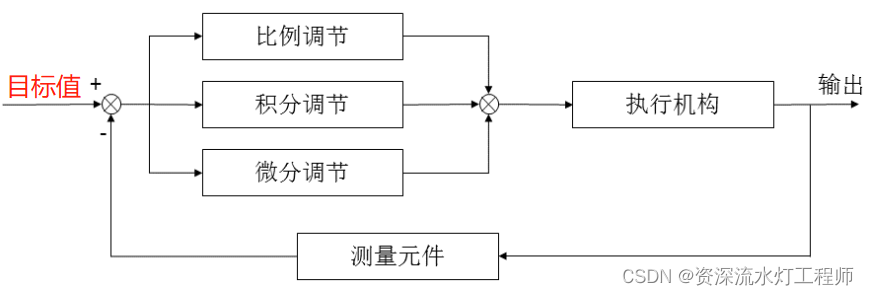
要想知道你的控制系统是否达到你的目标值，你需要干什么？当然是不断地看结果，比如温度控制系统，你通过加热的方式把一个铁块的温度控制在60℃，要想知道有没有达到这个目标温度，就需要搞一个温度传感器来测量铁块的温度，这个温度传感器就是测量元件。

温度传感器测量铁块温度的目的是什么？就是看铁块的温度是否到60℃了。怎么看，就是把这个测量值与目标值作比较，比大小，比出来的结果就叫误差。温度传感器测出来的温度就是反馈值，因为反馈值是不断地送到控制系统的，所以这个反馈值叫做输入更合适。

误差值 = 目标值 - 输入值

也可以写成这样： $Error = Setpoint - Input$

一般把 $Error$ 写成 $e$ ，也就是 $e = Setpoint - Input$

某个时刻的误差值可以写成 $e(t)$ , 也就是 $e(t) = Setpoint - Input$

控制系统的计算核心就是根据这个误差 $e(t)$ 来展开的,这个后面来展开。

比如温度传感器检测出来的温度是50摄氏度，误差Error = 60 - 50 = 10℃，这就表示温度还不够，还得继续加热，这个加热机构就是执行机构，这个执行机构可以是烧柴火，也可以是烧煤气，也可以是电加热条、电加热块......

不管是火、还是煤气、还是电，都只是个媒介，我们要的是控制思想。如果温度传感器测出来的温度是10度，远低于60℃，该怎么办，当然是把火烧旺点，电流加大点；如果温度传感器测出来的温度超过60℃，超过目标值了该怎么办，当然是把火或者电给关了。

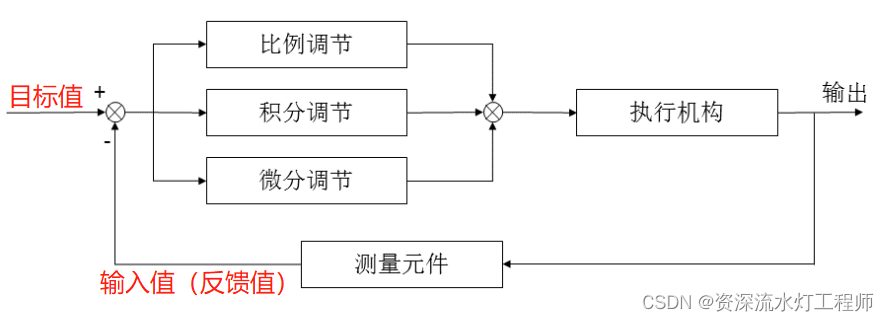
执行机构执行之后，也就是烧火，或者烧电之后，应该有个结果，这个结果就是铁块的温度，我们通过温度传感器来采集这个结果，并作为反馈值（输入值）送给控制机构，所以那个控制结构示意图还是有些欠妥，应该改为：

3、控制核心

前面说的温度比目标值小就加火加电，温度比目标值大就停火停电，这个加和停就是控制，要烧多大的火或者要放多大的电，这个量就是输出，PID控制就是控制这个火的大小，电的大小，从而达到控制温度的目的，所以，那个控制结构示意图应该这样标注：

PID的控制核心就是算一下该输出多大的火力或者电力，或者其他什么，反正都叫做输出（Output）。

现在大家应该都理解目标值、输入值（反馈值）、结果、输出、误差这些概念了，那个经典的公式应该可以出来了：

$Output = K_{p}*e(t) + K_{i}*\int e(t)d_{t} + K_{d}*\frac{de(t)}{d_{t}}$

这个 $Output$ 就是经过计算之后，应该输出的火力大小；

这个 $e(t)$ 就是前面所说的误差： $e(t) = Setpoint - Input$

比例、积分、微分

上面的经典公式又引入了3个新东西

这个 $K_{p}$ 就是比例系数（它是什么，要它干啥）

这个 $K_{i}$ 就是积分系数（它是什么，要它干啥）

这个 $K_{d}$ 就是微分系数（它是什么，要它干啥）

PID相关参数讲解：1、比例系数Kp与静态误差_资深流水灯工程师的博客-CSDN博客

PID代码实现

把这位外国网友的代码拿来分析一下，Arduino的某个PID库就是这哥们写的，原文链接如下

PID « Project Blog (brettbeauregard.com)

PID的开局都是这个公式：

$Output = K_{p}*e(t) + K_{i}*\int e(t)d_{t} + K_{d}*\frac{de(t)}{d_{t}}$

$e(t) = Setpoint - Input$

上面的公式是理想的情况，在代码实现的时候，需要将其离散化。

PID算法调用时间的分析

积分与微分与时间是直接相关的，咱也不提什么采样周期的事了，就是随机的调用PID算法，记录每次调用PID算法的时间间隔（timeChange）。

这个时间间隔（timeChange）就等于当前的时间减去上一次调用PID算法的时间：

$d_{t} = \Delta t = now-lastTime = timeChange$

所以累计

误差errSum

$errSum = \int e(t)d_{t}= e(0)*d_{t0} + e(1)*d_{t1} +e(2)*d_{t2}+...+e(t)*d_{t}$

用C语言表示累计误差可以是这样：

errSum += (error * timeChange);

误差的微分dErr,等于本次的误差减去上次一PID计算时的误差，除以时间间隔：

$dErr=\frac{de(t)}{d_{t}} =(error - lastErr)/timeChange$

综上，公式 $Output = K_{p}*e(t) + K_{i}*\int e(t)d_{t} + K_{d}*\frac{de(t)}{d_{t}}$ 用C语言表示出来可以是这样的：

Output = kp * error + ki * errSum + kd * dErr;

因为是随机的调用PID算法，所以需要记录每次PID计算时的时间点和误差

   lastErr = error;
   lastTime = now;

比例系数、积分系数、微分系数的设置函数实现

void SetTunings(double Kp, double Ki, double Kd)
{
   kp = Kp;
   ki = Ki;
   kd = Kd;
}

完整的PID实现代码如下所示

/*working variables*/
unsigned long lastTime;
double Input, Output, Setpoint;
double errSum, lastErr;
double kp, ki, kd;
void Compute()
{
   /*How long since we last calculated*/
   unsigned long now = millis();
   double timeChange = (double)(now - lastTime);

   /*Compute all the working error variables*/
   double error = Setpoint - Input;
   errSum += (error * timeChange);
   double dErr = (error - lastErr) / timeChange;

   /*Compute PID Output*/
   Output = kp * error + ki * errSum + kd * dErr;

   /*Remember some variables for next time*/
   lastErr = error;
   lastTime = now;
}

void SetTunings(double Kp, double Ki, double Kd)
{
   kp = Kp;
   ki = Ki;
   kd = Kd;
}

这个Compute（）函数是被不定期的调用，一般情况下效果也可以，能正常的工作起来，但距离工业应用还差的很远，还需要解决下面一系列的问题：