文档总目录

英文原文(Solving Sparse Linear Systems)

在Eigen中，有多种方法可用于求解稀疏系数矩阵的线性系统。由于此类矩阵的特殊表示，必须特别小心以获得良好的性能。有关Eigen中稀疏矩阵的详细介绍，请参见“[稀疏矩阵操作](#5.1 稀疏矩阵操作)”。本页列出了Eigen中可用的稀疏求解器。还介绍了所有这些线性求解器共同的主要步骤。根据矩阵的属性、所需的准确度，最终用户可以调整这些步骤以提高其代码的性能。请注意，并不需要深入了解这些步骤背后的内容：最后一节介绍了一个基础例程，可轻松使用以获取所有可用求解器的性能洞察。

稀疏求解器列表

Eigen 目前提供了一组广泛的内置求解器，以及外部求解器库的包装器。它们总结在下表中：

内置直接求解器

类及头文件	求解器种类	矩阵种类	与性能相关的功能	备注
SimplicialLLT #include<Eigen/SparseCholesky>	直接LLt分解	对称正定(SPD)	通过对矩阵的重排列、消元等操作，来减少生成的新元素，以减少计算时间和空间。（Fill-in reducing）	SimplicLDLT 通常更可取
SimplicialLDLT #include<Eigen/SparseCholesky>	直接 LDLt 分解	对称正定(SPD)	Fill-in reducing	推荐用于非常稀疏且不太大的问题（例如，2D 泊松方程）
SparseLU #include<Eigen/SparseLU>	LU 分解	方阵	快速的密集代数运算，包括基于GPU的加速、多线程优化、并行计算等。（Leverage fast dense algebra）、Fill-in reducing	针对不规则模式的大小问题进行了优化
SparseQR #include<Eigen/SparseQR>	QR 分解	矩形阵	Fill-in reducing	推荐用于最小二乘问题，具有基本的秩显示特性。

内置迭代求解器

类及头文件	求解器种类	矩阵种类	默认支持的预处理器	备注
ConjugateGradient #include<Eigen/IterativeLinearSolvers>	经典共轭梯度法（CG）	SPD	IdentityPreconditioner, [DiagonalPreconditioner], IncompleteCholesky	推荐用于大型对称问题（例如 3D 泊松方程）
LeastSquaresConjugateGradient #include<Eigen/IterativeLinearSolvers>	矩形阵最小二乘问题的 CG	矩形阵	IdentityPreconditioner, [LeastSquareDiagonalPreconditioner]	求解 $min
BiCGSTAB #include<Eigen/IterativeLinearSolvers>	迭代稳定双共轭梯度	方阵	IdentityPreconditioner, [DiagonalPreconditioner], IncompleteLUT	要加速收敛，请尝试使用 IncompleteLUT 预调节器。

• 共轭梯度法：（Conjugate Gradient method，简称CG），它是一种迭代求解线性方程组的方法。CG方法通常用于解决大规模稀疏对称正定线性方程组，具有高效、收敛快等优点。在Classic iterative CG中，每次迭代会得到一个新的解向量，同时利用前一次的残差和搜索方向来求解下一次的迭代解。

• 稳定双共轭梯度法：是求解非对称矩阵线性方程组（Ax = b）的迭代算法。与传统的共轭梯度法不同，稳定双共轭梯度法可以处理非对称矩阵的情况，并且在求解过程中，该方法可以保持数值稳定性，避免出现数值震荡等问题。该方法的主要思路是采用两条共轭的方向（与传统共轭梯度法相同）来求解线性方程组，但在每次迭代过程中，引入了一个稳定因子，该稳定因子的作用是保持迭代过程的数值稳定性。该稳定因子可以通过计算残差向量和搜索方向向量之间的内积来确定。

外部求解器的包装器

类	模块	求解器类型	矩阵类型	与性能相关的功能	依赖/证书	备注
PastixLLT PastixLDLT PastixLU	PaStiXSupport	Direct LLt, LDLt, LU factorizations	SPD SPD 方阵	Fill-in reducing, Leverage fast dense algebra, Multithreading	Requires the PaStiX package, CeCILL-C	针对棘手问题和对称模式进行了优化
CholmodSupernodalLLT	CholmodSupport	Direct LLt factorization	SPD	Fill-in reducing, Leverage fast dense algebra	Requires the SuiteSparse package, GPL
UmfPackLU	UmfPackSupport	Direct LU factorization	方阵	Fill-in reducing, Leverage fast dense algebra	Requires the SuiteSparse package, GPL
KLU	KLUSupport	Direct LU factorization	方阵	Fill-in reducing, suitted for circuit simulation	Requires the SuiteSparse package, GPL
SuperLU	SuperLUSupport	Direct LU factorization	方阵	Fill-in reducing, Leverage fast dense algebra	Requires the SuperLU library, (BSD-like)
SPQR	SPQRSupport	QR factorization	矩形阵	fill-in reducing, multithreaded, fast dense algebra	Requires the SuiteSparse package, GPL	推荐用于最小二乘问题，具有基本的秩显示特性。
PardisoLLT PardisoLDLT PardisoLU	PardisoSupport	Direct LLt, LDLt, LU factorizations	SPD SPD 方阵	Fill-in reducing, Leverage fast dense algebra, Multithreading	Requires the Intel MKL package, Proprietary	针对棘手问题模式进行了优化，另请参阅将 MKL 与 Eigen 结合使用
AccelerateLLT AccelerateLDLT AccelerateQR	AccelerateSupport	Direct LLt, LDLt, QR factorizations	SPD SPD 方阵	Fill-in reducing, Leverage fast dense algebra, Multithreading	Requires the Apple Accelerate package, Proprietary

这里SPD的意思是对称正定。

稀疏求解器概念

所有这些求解器都遵循相同的一般概念。这是一个典型且普遍的例子：

#include <Eigen/RequiredModuleName>
// ...
SparseMatrix<double> A;
// fill A
VectorXd b, x;
// fill b
// solve Ax = b
SolverClassName<SparseMatrix<double> > solver;
solver.compute(A);
if(solver.info()!=Success) {
  // decomposition failed
  return;
}
x = solver.solve(b);
if(solver.info()!=Success) {
  // solving failed
  return;
}
// solve for another right hand side:
x1 = solver.solve(b1);

对于 SPD 求解器，第二个可选模板参数允许指定使用哪个三角形部分，例如：

#include <Eigen/IterativeLinearSolvers>
 
ConjugateGradient<SparseMatrix<double>, Eigen::Upper> solver;
x = solver.compute(A).solve(b);

在上面的例子中，仅考虑输入矩阵A的上三角部分进行求解。相反的三角形可能为空，也可能包含任意值。

如果必须解决具有相同稀疏模式的多个问题，则“计算”步骤可以分解如下：

SolverClassName<SparseMatrix<double> > solver;
solver.analyzePattern(A);  // for this step the numerical values of A are not used
solver.factorize(A);
x1 = solver.solve(b1);
x2 = solver.solve(b2);
...
// modify the values of the nonzeros of A, the nonzeros pattern must stay unchanged
A = ...; 
solver.factorize(A);
x1 = solver.solve(b1);
x2 = solver.solve(b2);
...

compute() 方法相当于同时调用 analyzePattern() 和 factorize()。

每个求解器都提供一些特定的功能，例如行列式、对因子的访问、迭代的控制等。更多详细信息可在相应类的文档中找到。

最后，大多数迭代求解器也可以在无矩阵上下文中使用，请参阅以下示例。

计算步骤

solve() 函数计算具有一个或多个右侧的线性系统的解。

X = solver.solve(B);

在这里，B可以是一个向量或一个矩阵，其中列组成不同的右侧。solve() 函数也可以被多次调用，例如当所有的右侧不是一次性提供的时候。

x1 = solver.solve(b1);
// Get the second right hand side b2
x2 = solver.solve(b2); 
//  ...

对于直接方法，解是以机器精度计算的。有时候，解不需要太精确。在这种情况下，迭代方法更加适用，并且可以在解步骤之前使用setTolerance()设置所需的精度。有关所有可用函数，请参阅迭代求解器模块的文档。

基准测试例程

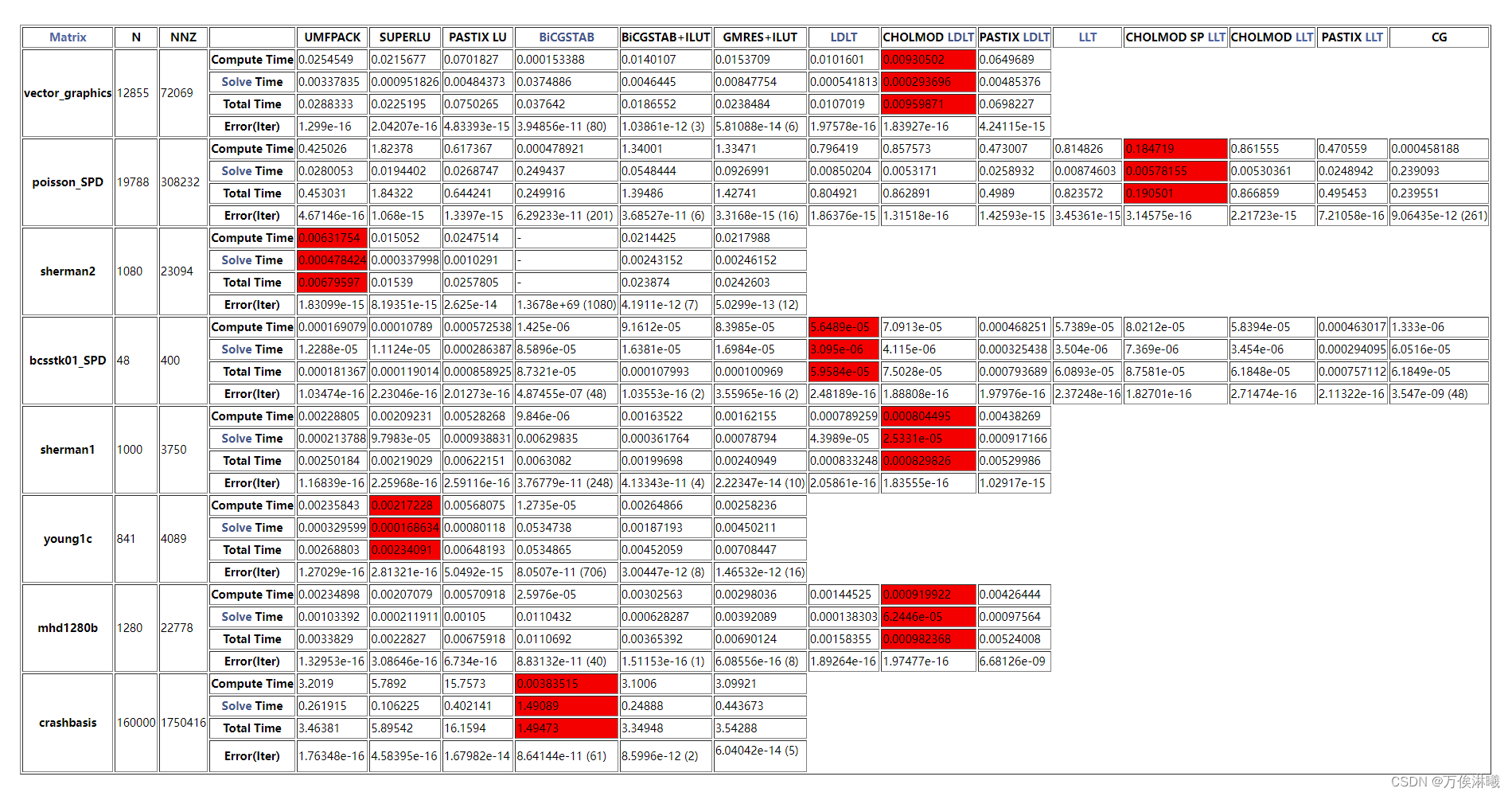
大多数情况下，只需要知道求解系统需要多长时间，以及希望使用哪种最适合的求解器。在Eigen中，提供了一个可用于此目的的基准测试例程。在构建目录中，切换到 bench/spbench 并通过键入 make spbenchsolver 来编译该例程。使用 --help 选项运行它以获取所有可用选项的列表。基本上，要测试的矩阵应该遵循 MatrixMarket 坐标格式，并且该例程返回Eigen中所有可用求解器的统计信息。

要以 MatrixMarket 格式导出矩阵和右侧向量，可以使用不受支持的 SparseExtra 模块：

#include <unsupported/Eigen/SparseExtra>
...
Eigen::saveMarket(A, "filename.mtx");
Eigen::saveMarket(A, "filename_SPD.mtx", Eigen::Symmetric); // if A is symmetric-positive-definite
Eigen::saveMarketVector(B, "filename_b.mtx");

下表给出了来自几个 Eigen 内置和外部求解器的 XML 统计信息的示例：