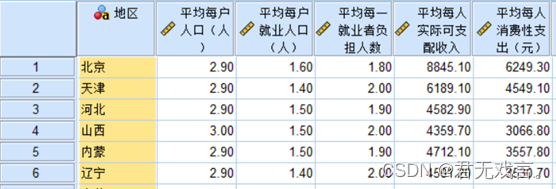
| 实验目的: 1.掌握主成分分析的基本思想; 2.熟悉掌握SPSS软件进行主成分分析的基本操作; 3.利用实验指导的实例数据,上机熟悉主成分分析方法. 实验内容: 下表是我国2005年第1、2季度各地区城镇居民家庭收支基本情况的统计数据。根据这些数据进行主成分分析,并依据分析结果对地区城镇居民家庭收支情况进行排序和分类。
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 实验前预习: 主成分分析的基本思想; SPSS软件进行主成分分析的基本操作; | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
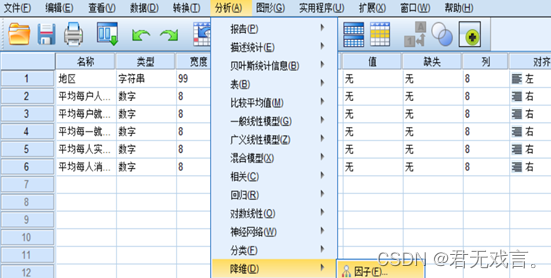
| 程序测试、运行结果及分析: 主成分分析 (我国2005年第1、2季度各地区城镇居民家庭收支基本情况) 操作步骤:
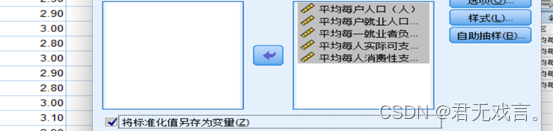
勾选“将标准化值另存为变量”
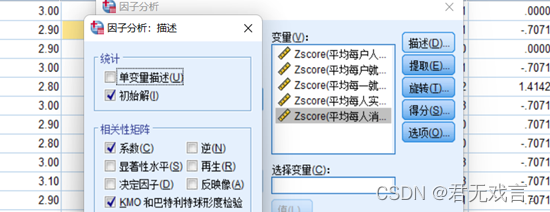
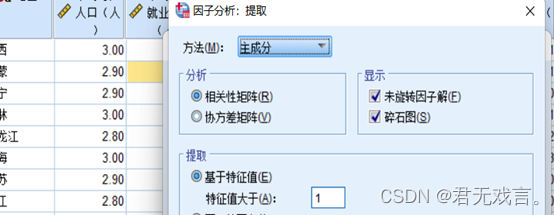
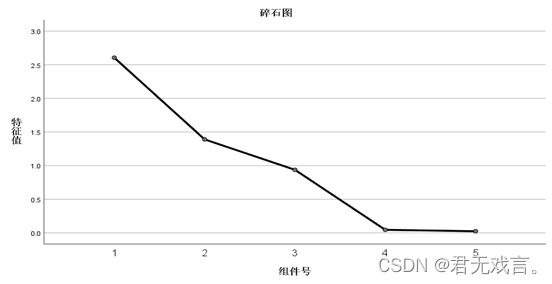
点击提取,方法选择为主成分,勾选碎石图。
最后点击继续和确定。 运行结果与分析:
由KMO 和巴特利特检 由KMO 和巴特利特检验p值小于0.05则表示有显著性,而KMO取样适切性量数。大于0.6比较适合,但其值为0.377所以数据不适合做主成分分析。
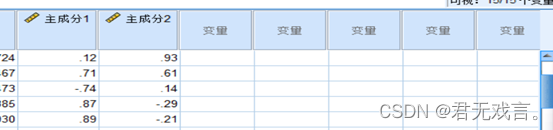
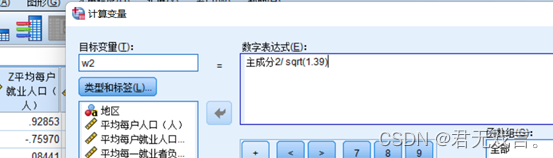
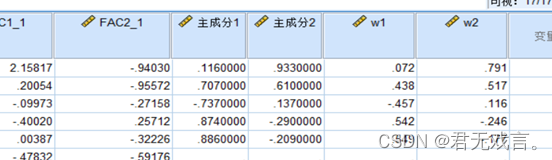
主成分得分公式为f=w1*x1+w2*x2+…+wn*xn其中wj=为主成分矩阵的值与该成分特征值(2.605和0.390)的开根值,代表权重。每个主成分矩阵的值都要除以该成分特征值的开根值得到主成分公式的系数。 再次输入成分矩阵的系数数据
最终的到主成分F1和F2的系数w1和w2
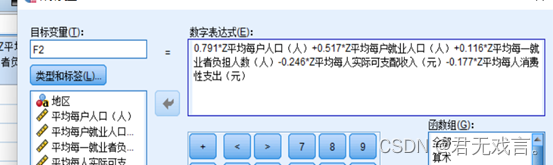
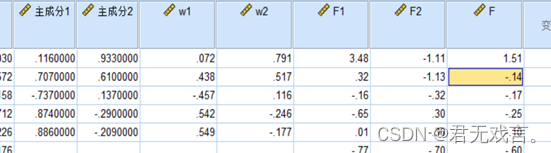
所以主成分方程为: F1=0.072*x1 +0.438*x2-0.457*x3+0.542*x4 +0.549*x5 F2=0.791*x1+0.517*x2 +0.116*x3-0.246*x4-0.177*x5 综合得分为:(其系数来源于两个主成分对总体的贡献度) F=0.521*F1+0.278*F2 然后通过spss计算F的具体数值
对最后F值进行排序,便可以对对应城市进行排序,最终得到如下城市排名:
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 讨论:
1、主成分分析能降低所研究的数据空间的维数。即用研究m维的Y空间代替p维的X空间(m <p),而低维的Y空间代替高维的x空间所损失的信息很少。 2、有时可通过因子负荷的结构,弄清X变量间的某些关系。 3、多维数据的一种图形表示方法。 4、由主成分分析法构造回归模型。把各主成分作为新自变量代替原来自变盈X做回归分析。 5、用主成分分析筛选回归变量。回归变量的选择有着重的实际意义,为了使模型本身易于做结构分析、控制和预报,好从原始变量所构成的子集合中选择最佳变量,构成最佳变量集合。用主成分分析筛选变量,可用较少的计算量来选择量,获得选择最佳变量子集合的效果。
主成分得分公式为f=w1*x1+w2*x2+…+wn*xn其中wj=为主成分矩阵的值与该成分特征值(2.605和0.390)的开根值,代表权重。每个主成分矩阵的值都要除以该成分特征值的开根值得到主成分公式的系数。 最后的综合得分为每个主成分与其对总体的贡献度百分比的乘积之和即(其系数来源于两个主成分对总体的贡献度)F=a1*F1+a2*F2+…+an*Fn对综合得分进行排序便可以对最终所对应的数据进行排名。 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
基于spss的多元统计分析 之 主成分分析(5/8)
news2026/2/11 12:30:19
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如若转载,请注明出处:http://www.coloradmin.cn/o/673886.html
如若内容造成侵权/违法违规/事实不符,请联系多彩编程网进行投诉反馈,一经查实,立即删除!相关文章
【C++篇】OOP中部分:继承和派生
友情链接:C/C系列系统学习目录 知识总结顺序参考C Primer Plus(第六版)和谭浩强老师的C程序设计(第五版)等,内容以书中为标准,同时参考其它各类书籍以及优质文章,以至减少知识点上的…
2023年05月份青少年软件编程Python等级考试试卷六级真题(含答案)
2023-05 Python六级真题 分数:100 题数:38 测试时长:60min
一、单选题(共25题,共50分)
1. 明明每天坚持背英语单词,他建立了英语单词错题本文件“mistakes.txt”,将每天记错的单词增加到该文件中&#x…
ROS:launch文件演示
目录 前言一、添加launch文件夹二、新建launch文件三、编辑launch内容四、 执行文件 前言
一个程序中可能需要启动多个节点,比如:ROS 内置的小乌龟案例,如果要控制乌龟运动,要启动多个窗口,分别启动 roscore、乌龟界面节点、键盘…
【数据分享】1929-2022年全球站点的逐日降雪深度数据(Shp\Excel\12000个站点)
气象数据是在各项研究中都经常使用的数据,气象指标包括气温、风速、降水、能见度等指标,说到气象数据,最详细的气象数据是具体到气象监测站点的数据!
对于具体到监测站点的气象数据,之前我们分享过1929-2022年全球气象…
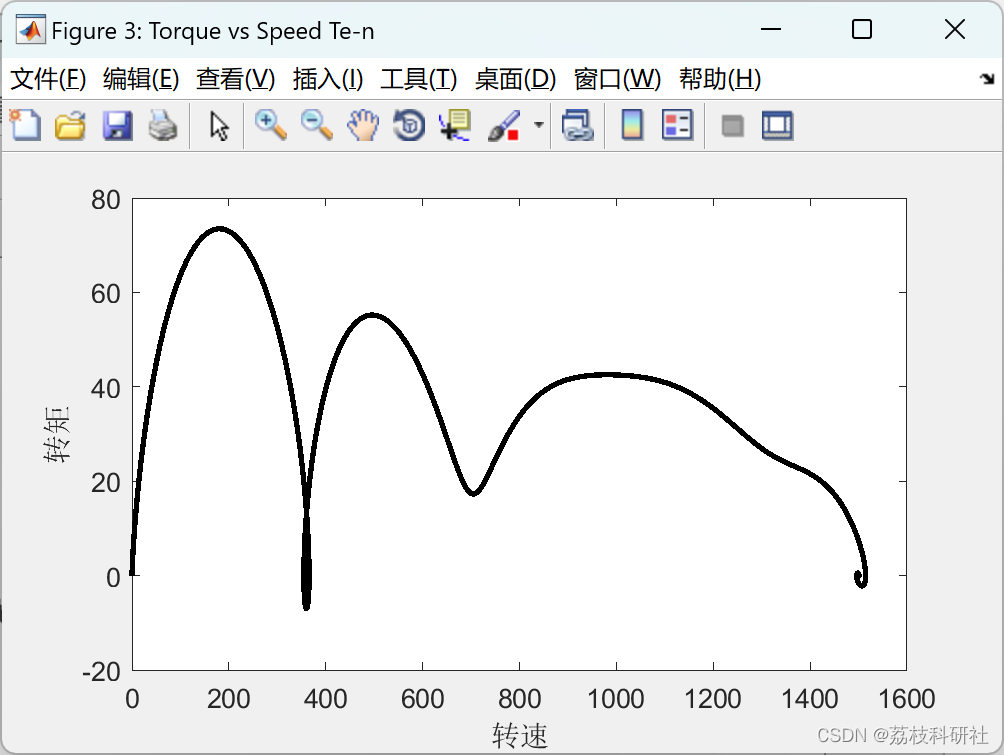
感应电动机起动动态计算(Matlab代码实现)
💥💥💞💞欢迎来到本博客❤️❤️💥💥 🏆博主优势:🌞🌞🌞博客内容尽量做到思维缜密,逻辑清晰,为了方便读者。 ⛳️座右铭&a…
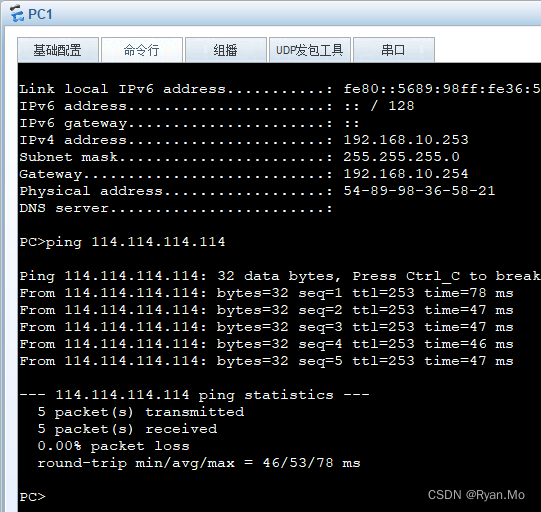
#家庭网络配置(华为路由与交换机)
#家庭网络配置 #三层交换机配置 #打开HDCP功能 #进入系统视图 <Huawei>system-view #关闭系统提示信息 [Huawei]undo info-center enable #打开DHCP 使能 [Huawei]dhcp enable #创建vlan 10 vlan 20 vlan 2 [Huawei]vlan batch 2 10 20 #进入 vlan 并配置ip 与 dhcp […
【机器学习】十大算法之一 “神经网络”
作者主页:爱笑的男孩。的博客_CSDN博客-深度学习,活动,python领域博主爱笑的男孩。擅长深度学习,活动,python,等方面的知识,爱笑的男孩。关注算法,python,计算机视觉,图像处理,深度学习,pytorch,神经网络,opencv领域.https://blog.csdn.net/Code_and516?typeblog个…
使用Postman模拟文件上传和下载
介绍
Postman是一款强大的HTTP请求模拟工具,它可以帮我们在没有前端界面的情况下模拟发送HTTP请求,非常适合API开发和测试。在本篇文章中,我将向你展示如何使用Postman进行文件的上传和下载。
文件上传 启动Postman,点击“新建请…
Linux的基础操作
0.前言
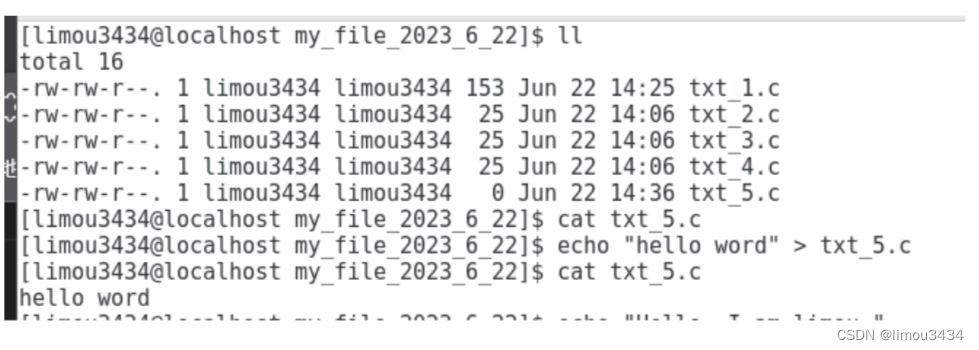
您好,这里是limou3434的一篇关于Linux基础操作的博文。感兴趣的话,可以看看我的其他博文系列。本次我给您带来的是Linux下的几个基础命令,学会这些命令您就可以开始在Linux管理和操作一些文件了。
注意:本次演示环境是在…
【HTML】常用标签
文章目录 1.标题字标签h1-h62.段落标签p3.换行标签br4.格式化标签5.图片标签6.超链接标签a7.表格标签单元格合并行合并列合并 8.无序列表9.有序列表10.自定义列表11.表单标签11.1 form标签11.2 表单控件11.2.1 input标签11.2.2 label标签11.2.3 select标签11.2.4 textarea标签 …
2023年为什么你需要学习GPU?
2023年为什么你需要学习GPU?掌握这一绝对重要的技能,开启你的未来之旅! 亲爱的朋友们,时光飞逝,2023年已经悄然而至。在这个充满机遇和挑战的数字时代,学习GPU成为了你无法忽视的重要任务。为什么呢&#x…
《大话设计模式》笔记
1. 简单工厂模式
1.1 面向对象的好处
考虑通过封装、继承、多态把程序的耦合度降低,使用设计模式使得程序更加的灵活,容易修改,并且易于复用。
1.2 复制 Vs 复用
有人说初级程序员的工作就是 CtrlC 和 CtrlV,这其实是非常不好…
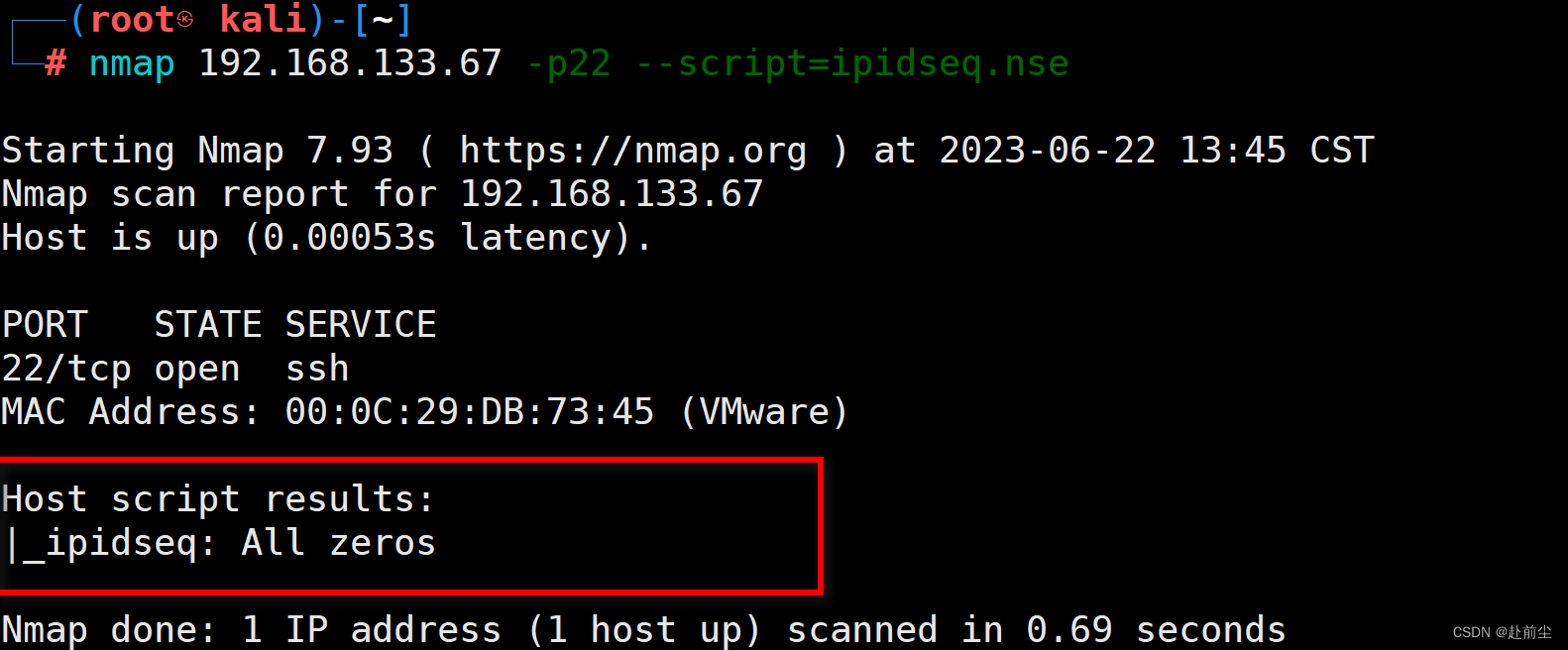
通过僵尸扫描判断目标主机端口开放状态
环境准备 使用scapy工具发包 攻击主机IP: 192.168.133.66 僵尸主机IP: 192.168.133.67 ,僵尸主机不主动与任何机器通信,且满足IP数据包ID自增** 注:用nmap 判断主机是否满足僵尸主机条件,一般早期的windwos XP系统IP数据包ID…
MySQL优化--主从同步,分库分表
目录
MySQL主从同步原理 MySQL主从复制的核心就是二进制日志
面试回答
分库分表
分库分表的时机
分库分表的策略
垂直分库
垂直分表
水平分库
水平分表
分库分表的策略
分库之后的问题
面试回答 MySQL主从同步原理
如果项目上线了,通常情况下…
【Python开发】FastAPI 11:构建多文件应用
以往的文件都是将对外接口写在一个文件里边,而作为应用来说,接口是不可避免分散到多个文件中的,比如某文件负责注册登录模块,某文件负责内管模块,某文件负责业务模块等。FastAPI 也提供了APIRouter 这一工具来进行灵活…
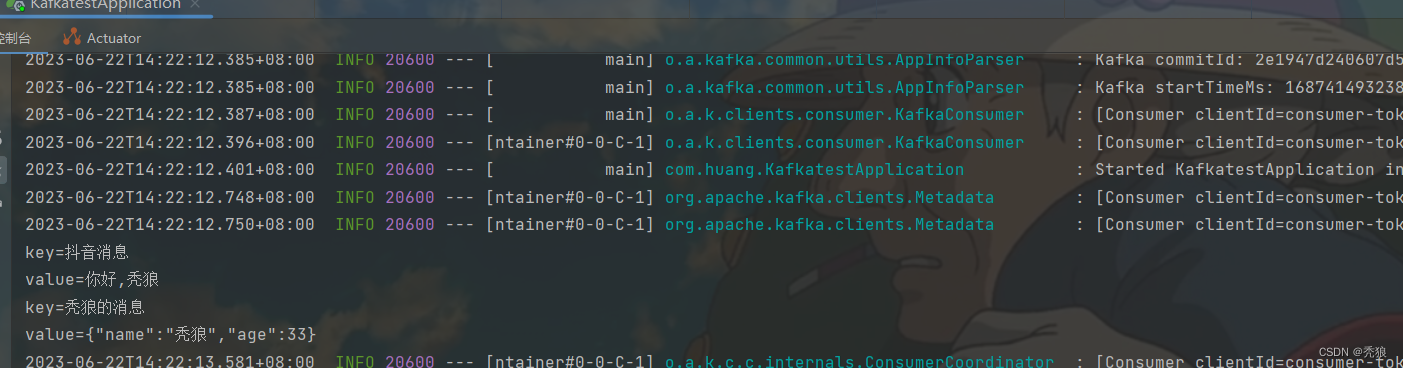
kafka消息队列的初步探索
消息队列的作用就是提高运行速度,防止线程堵塞。
kafka的作用 异步 通过在消息队列发送消息的方式,将对应的业务作为监听者,此时我们只需要考虑发送消息的时间即可,大大提高了运行的速度。 解耦 如果使用原来的直接调用对应业务的…
【libdatachannel】pycharm运行streamer的信令服务及streamer与js客户端联调
启动py服务器
ssl必须额外指定 # Usage: ./server.py [[host:]port] [SSL certificate file]文档给出了服务的启动命令: python3 -m http.server --bind 127.0.0.1 8080 直接运行: python的信令服务 #!/usr/bin/env python
#
# Python signaling server…
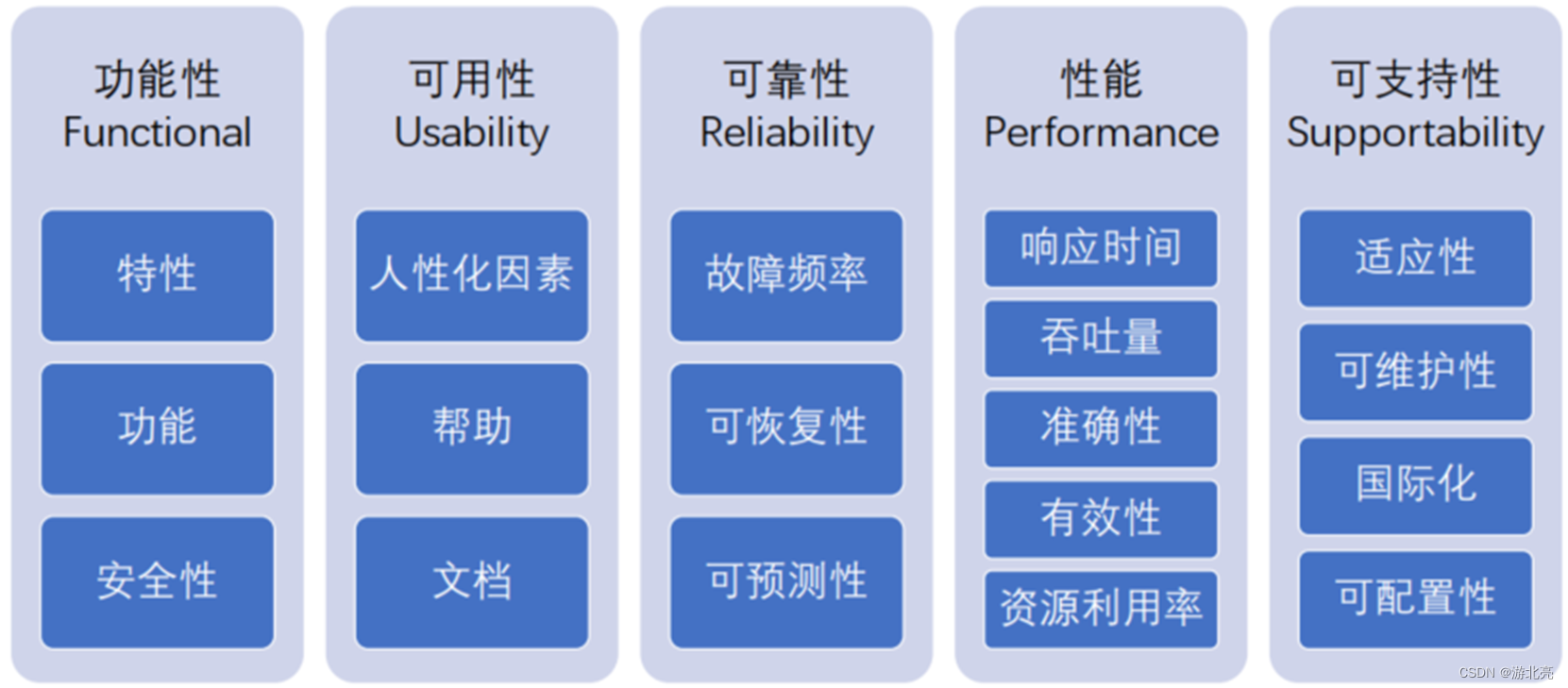
需求分析引言:架构漫谈(二)非功能性需求
上一篇文章,简要介绍了架构的概念和架构设计流程,并简单介绍了需求分析的内容, 并在最后指出:需求分析的产出物,要包括非功能性需求,常见的非功能性需求如下:
完成任务的速度结果的精度操作的安…
MySQL实战解析底层---为什么表数据删掉一半,表文件大小不变
目录
前言
参数innodb_file_per_table
数据删除流程
重建表
Online 和 inplace 前言 数据库占用空间太大,我把一个最大的表删掉了一半的数据,怎么表文件的大小还是没变?这与数据库表的空间回收有关这里还是针对MySQL中应用最广泛的InnoD…
结构型设计模式07-享元模式
🧑💻作者:猫十二懿 ❤️🔥账号:CSDN 、掘金 、个人博客 、Github 🎉公众号:猫十二懿 享元模式
1、享元模式介绍
享元模式是一种结构型设计模式,旨在**通过共享对象来减少内存使…