一、介绍

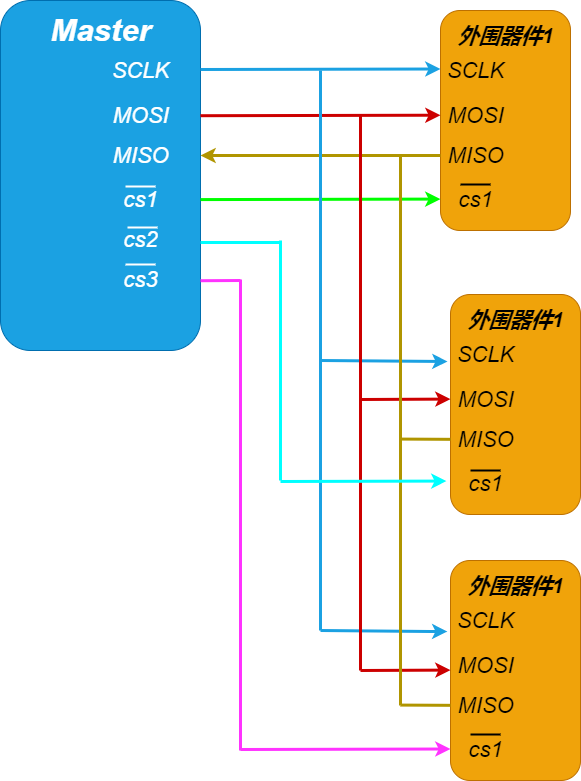
只能观察范围信息的传感器无法通过单次检测提供对物体状态的完整了解。此外，当以笛卡尔坐标系表示时，仅范围测量的不确定性是非高斯的，并产生凹形。对于具有窄视场（FOV）的仅范围传感器，角度不确定性很小，可以通过椭球体（即高斯分布）近似。然而，对于具有宽视场的仅范围传感器，当以笛卡尔框架表示时，不确定性由凹环形状描述，这不容易用椭球体近似。如下图所示。

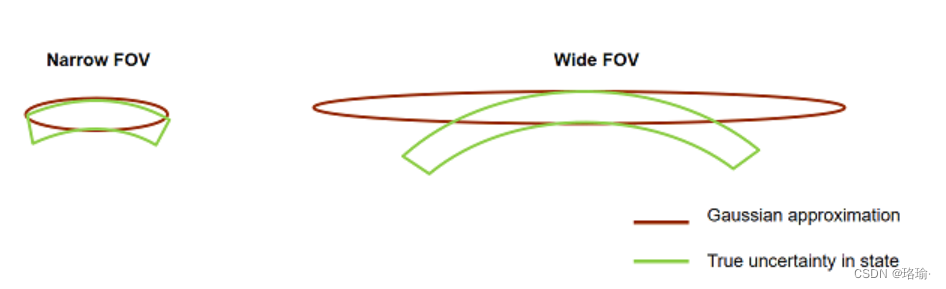
这种现象在远程雷达中也观察到，它们提供方位角和距离信息。当每个方位角分辨率像元的 FOV 跨越空间中的大区域时，状态的分布变为非高斯分布。在这些情况下，通常采用远程校正等技术来使用高斯滤波器，如扩展卡尔曼滤波器和无迹卡尔曼滤波器。

在此示例中，将学习如何使用粒子滤波器和高斯和滤波器来表示由大型 FOV 传感器的范围测量引起的状态中的非高斯不确定性。

二、定义方案

该场景模拟了在 X-Y 平面中以恒定速度行进的单个对象。该物体穿过三个间距相等的传感器的覆盖区域，方位角的FOV为60度。传感器 FOV 重叠，当对象穿过重叠区域时，这增强了可观察性。每个传感器报告测量范围测量值，测量精度为 5 厘米。

三、使用粒子过滤器进行跟踪

在本节中，粒子过滤器用于跟踪对象。跟踪由单假设跟踪器使用执行。跟踪器负责维护轨道，同时减少误报的数量。

该函数初始化等速粒子滤波器，但限制了从 [-180 180] 到本问题中已知传感器 FOV 的方位角和 [-90 90] 仰角 [-90 90]的角度。

粒子沿仅范围测量弧的状态具有非高斯不确定性，直到目标被下一个传感器检测到。当目标穿过传感器覆盖区域的边界时，与其他粒子相比，边界处出现粒子的可能性增加。这种可能性的增加触发了粒子过滤器中的重采样步骤，粒子坍缩到真正的目标位置。

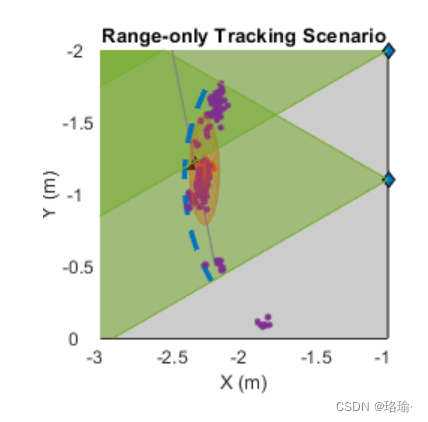
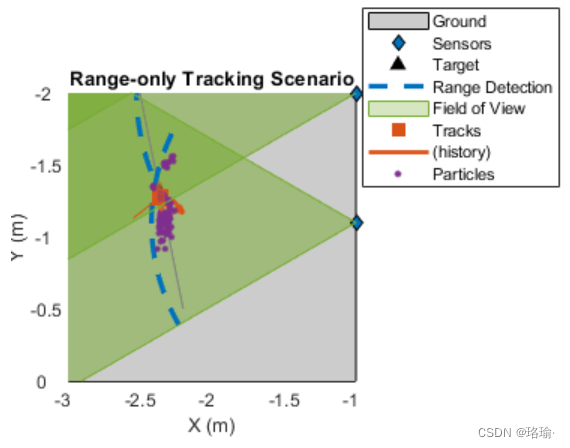
使用粒子过滤器，跟踪器在方案期间维护跟踪。

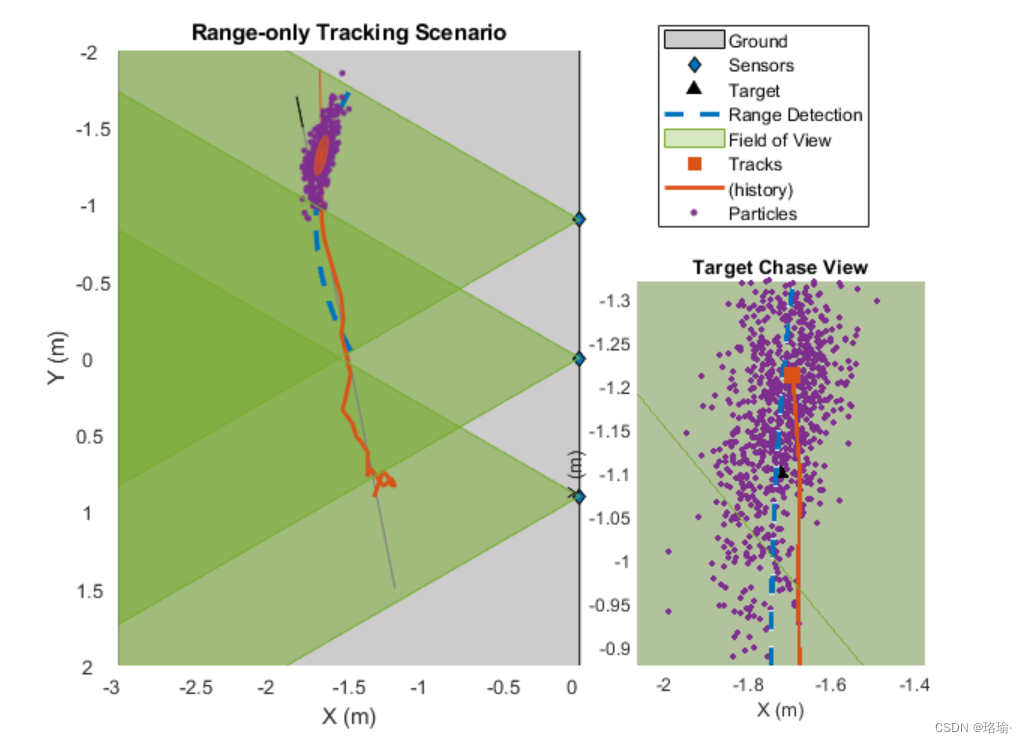
四、使用高斯和滤波器进行跟踪

在本节中，高斯和滤波器用于跟踪对象。对于仅范围测量，可以使用初始化。该函数初始化角度参数化扩展卡尔曼滤波器。此示例中定义的函数修改该函数以跟踪缓慢移动的对象。

可以使用属性来查看每个扩展卡尔曼滤波器的状态。在下图中由“单个滤镜”表示，请注意滤光片如何沿着仅范围测量生成的弧线对齐，直到目标到达重叠区域。越过边界后，滤波器在边界处的可能性立即增加，轨道会收敛到该单个滤波器。与最接近边界的滤波器相比，其他单个滤波器的权重下降，并且它们对状态估计的贡献减小。

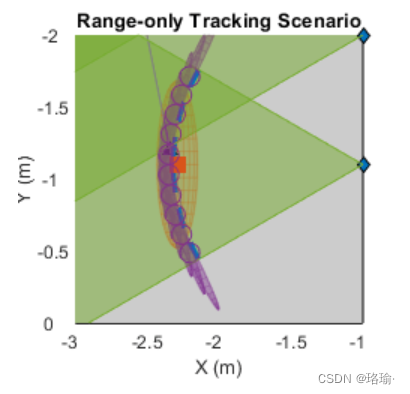
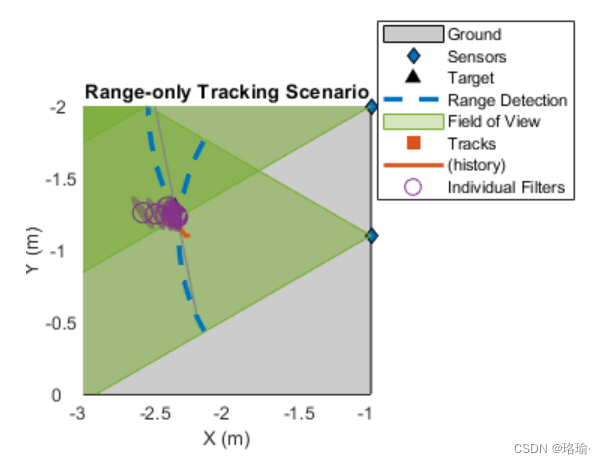
使用高斯和滤波器，跟踪器在方案期间维护跟踪。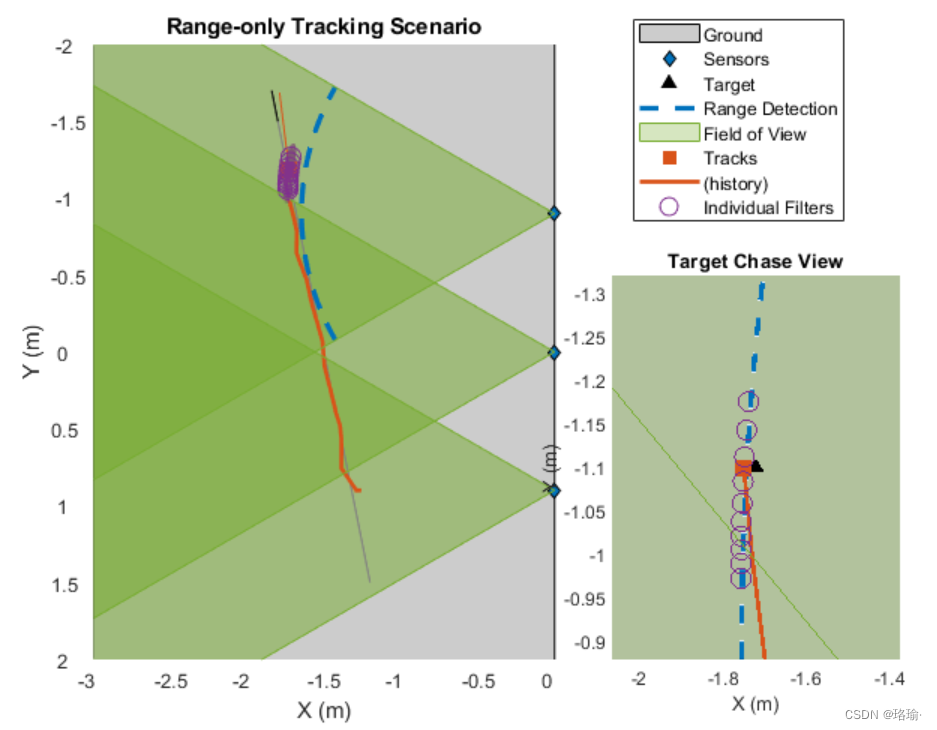

五、总结

在此示例中，学习了如何使用粒子滤波器和高斯和滤波器来跟踪使用仅范围测量值的对象。粒子滤波器和高斯和滤波器都提供了跟踪遵循非高斯状态分布的对象的功能。高斯和滤波器通过高斯分量的加权和近似分布，而粒子滤波器则通过一组样本表示这种分布。粒子过滤器提供了一种更自然的方法来表示任何任意分布，只要可以从中生成样本。然而，为了完美地表示分布，可能需要大量的粒子，这增加了使用过滤器的计算要求。由于状态由样品描述，粒子滤波器结构允许使用任何过程噪声分布以及测量噪声。相比之下，高斯和滤波器对每个分量使用高斯过程和测量噪声。颗粒的主要缺点之一是“样品贫乏”的问题。重采样后，粒子可能会坍缩到可能性很高的区域，不允许过滤器从“不正确”的关联中恢复。由于在高斯和滤波器中不执行重采样，并且每个状态都是高斯的，因此高斯和滤波器提供了一些从这种关联中恢复的能力。然而，这种恢复通常取决于每个高斯分量的权重和协方差。