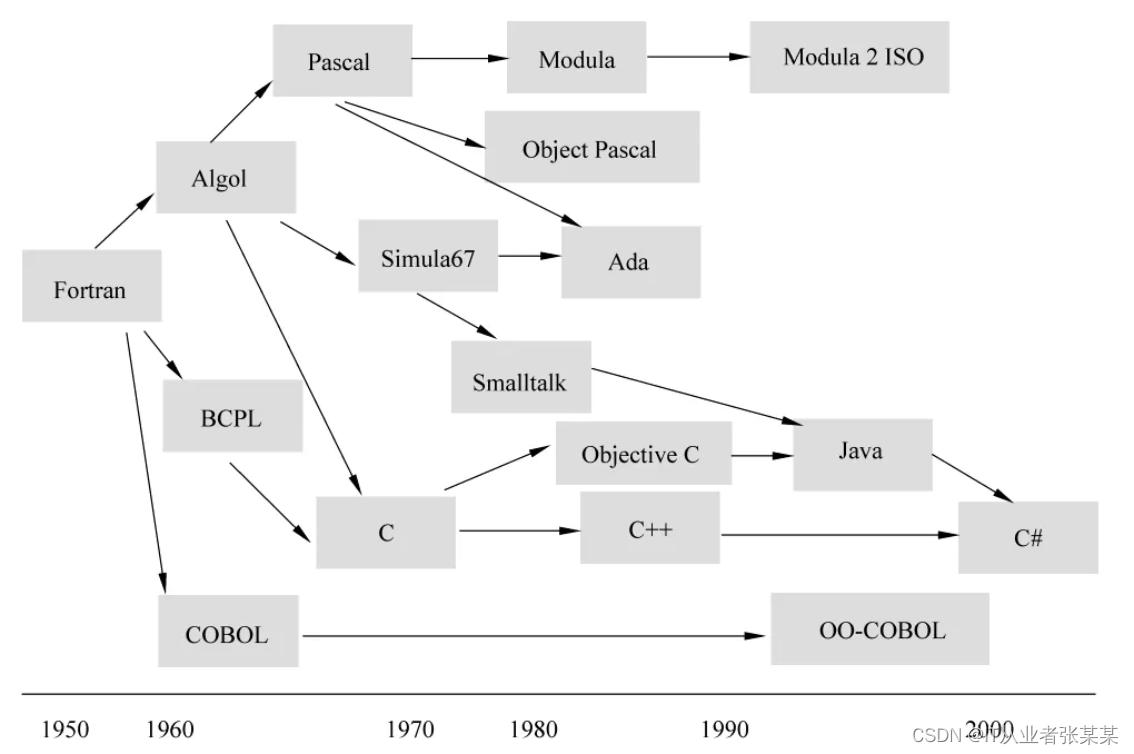
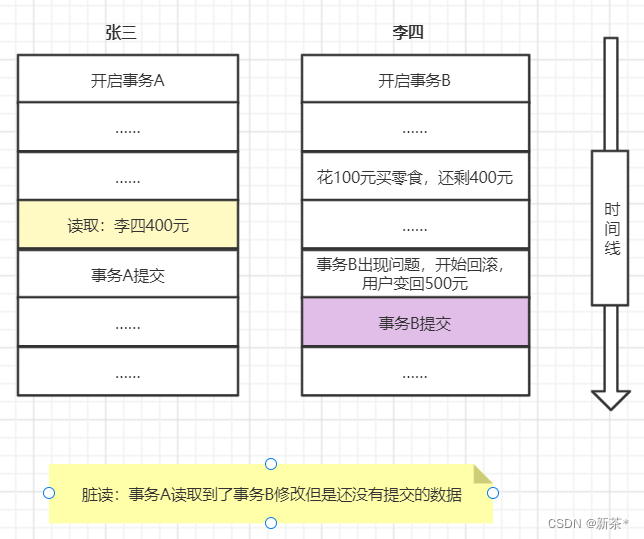
下图为串扰的电路模型，动态线与静态线之间通过互容与互感联系，这样也说明了动态线的信号耦合到静态线上的条件是存在di/dt或者dv/dt时，也就是说只在信号边沿上产生串扰，当电压或者电流为常数的时候静态线上就不会有串扰的信号。

信号前沿可以看作导线的电流源，在整个前沿的时刻，流经互容的总电流为：

                                                   Ic=Cm*dV / dt

Cm为上升沿时间段长度的耦合电容，dt为上升沿时间，dV为信号电压。

又有Cm=Cml*△X = Cml*v*RT，Cml为单位长度的互容，v为信号的传输速度，RT为信号的上升边沿，那么在整个容性耦合电流就为：

                                                   Ic= Cml*v*V

从上面的表达式可以看出容性耦合电流的大小与信号的上升时间是没有关系的，我们常常会认为上升沿越短，dV / dt越大容性耦合电流也就越大，这其实是错误的，因为上升沿短会使上升沿时间段长度的耦合电容Cm变小，所以容性耦合电流是和单位长度的互容直接相关的。

以此类推可以知道感性耦合电压为：

                                                   VL= Lml *v*I

Lml为单位长度的互感，v为信号的传输速度，I为信号的电流。

综上我们可以得出：

1>瞬时的容性耦合电流噪声、感性耦合的电压噪声大小都直接取决于信号的强度，信号越强，耦合的噪声就越大。

2>单位长度的互感或者互容越大，耦合的噪声就越大。

3>信号的传输速度越快，上升沿时间段的耦合长度就越大，耦合到的噪声越大。

4>耦合噪声的强弱和信号的上升沿时间没有关系。因为上升沿短了以后，上升沿时间段的耦合长度也变短了，耦合长度短了以后，这段长度的总互感、互容也变小了。