一、题目分析
问题描述
麦克结婚后,在上个月他胖了70磅。因为手指上的脂肪过多,使他连给他最亲密的朋友斯拉夫克写一个电子邮件都很困难。
每晚麦克都详细地描述那一天他所吃的所有东西,但有时当他只想按一次某键时往往会按了不止一次,并且他的胖手指还会碰到他不想要按的键,麦克也知道自己的手指有问题,因此他在打字的时候很小心,以确保每打一个想要的字符时误打的字符不超过3个,误打的字符可能在正确字符之前也可能在其之后。
当斯拉夫克多次收到读不懂的电子邮件后,他总是要求麦克将电子邮件发3遍,使他容易读懂一点。
问题分析
本题要求解三个序列的最长公共子序列。
二、功能的设计与思路
根据题意,麦克每打一个想要的字符时,误打的字符不超过3个,误打的字符可能在正确字符之前也可能在其之后。因此,两个正确的字符之间最多间隔六个错误的字符。用f[i][j][k]表示三个字符串到达[i][j][k]位置时的最长字符,如果ijk位置的字符相同,从[i-7][j-7][k-7]的位置开始循环,求出此间最长公共子序列,再加上当前的字符即可。
求最长公共子序列,在应用分治思想,将大问题分解成几个部分之后,因为对同样问题的重复计算,即递归效率太低,故采用动态规划,其具体步骤为:
Step1:找出最优解的性质,并刻划其结 构特征。
Step2:递归地定义最优值。
Step3:以自底向上的方式计算出最优值。
Step4:根据计算最优值时得到的信息,构造最优解。
- 算法设计与分析
假设S1= {1…n},S2 = {1…m}(m,n不一定相等,C= {1…i}是最长公共子串。
如果S1[n] = S2[m],则有S1[n] = S2[m] = C[i];所以 C[1…i] = C[1…i-1] +1;
如果S1[n] != S2[m],分三种情况讨论:
S1[n] = C[i],S2[m] != C[i], 所以C是S2={1…m-1}的子串。
S1[n] != C[i],S2[m] = C[i], 所以C是S1={1…n-1}的子串。
S1[n] != C[i],S2[m] != C[i], 所以C是S2={1…m-1}与S1={1…n-1}的子串。
所以C{1…i} = Max最长子串(S1={1…n-1},S2={1…m})或者是Max最长子串(S1={1…n},S2={1…m-1});
换句话说就是最长公共子串的子串一定是原字符串的某子串的最长公共子串。如果设LCS(S1,S2,i,j)表示S1[1…i]和S2[1…j]的最长公共子序列的长度,则有:
if(S1[i,j] ==S2[i,j])
C[i,j] = LCS(S1,S2,i-1,j-1);
else
C[i,j] = Max(LCS(S1,S2,i-1,j),LCS(S1,S2,i,j-1));
若用c[i][j]记录两个序列的最长公共子序列的长度。其递归结构公式为:
|
|
但是就本题而言需要对三个序列求解公共子序列,所以得对上诉结构公式进行推广
f[i][j][l]表示第一个字符串的前i个字符与第二个字符串的前j个字符以及第三个字符串前l个字符组成的最长公共子序列。
接着,我们可以得出以下结论:
(1)当i,j,l任意一者等于0时,f[i][j][l]=0。(前0个,也就是没有嘛)
(2)当A[i-1]==B[j-1]&&B[j-1]==C[l-1]时(A,B,C分别表示三个字符串),f[i][j][l]就等于A的前i-1个字符,B的前j-1个字符,C的前l-1个字符组成的最长公共子序列+1,即f[i][j][l]=f[i-1][j-1][l-1]+1。
(3)若以上两种情况都不满足,我们就可以在以下几种情况中求最大值
<1>f[i-1][j][l]
<2>f[i][j-1][l]
<3>f[i][j][-1l]
<4>f[i-1][j-1][l]
<5>f[i-1][j][l-1]
<6>f[i][j-1][l-1]
<7>f[i-1][j-1][l-1]
简单的来说,就是看哪种情况的最长公共子序列最长。
若用f[i][j][l]记录序列a和b和c的最长公共子序列的长度。
据此性质得到其递归结构的伪代码为
for (int i=1;i<=lena;i++)
for (int j=1;j<=lenb;j++)
for (int l=1;l<=lenc;l++)
f[i][j][l]="";
for (int i=1;i<=lena;i++)
for (int j=1;j<=lenb;j++)
for (int k=1;k<=lenc;k++)
if (a[i]==b[j]&&b[j]==c[k]){
f[i][j][k]=a[i];
for (int x=max(0,i-7);x<i;x++)
for (int y=max(0,j-7);y<j;y++)
for (int z=max(0,k-7);z<k;z++)
if (f[i][j][k].size()<=f[x][y][z].size()+1)
f[i][j][k]=f[x][y][z]+a[i];
if (ans.size()<=f[i][j][k].size())
ans=f[i][j][k];
}
cout<<ans<<endl;
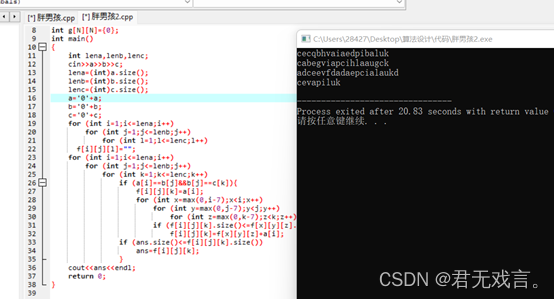
- 代码实现
#include<iostream>
#include<algorithm>
#include<cstdio>
#include<string>
using namespace std;
const int N=105;
string f[N][N][N],a,b,c,ans="";
int g[N][N]={0};
int main()
{
int lena,lenb,lenc;
cin>>a>>b>>c;
lena=(int)a.size();
lenb=(int)b.size();
lenc=(int)c.size();
a='0'+a;b='0'+b;c='0'+c;
int i,j,k;
for(i=1;i<=lena;i++)
for(j=1;j<=lenb;j++)
for(k=1;k<=lenc;k++)
f[i][j][k]="";
for(i=1;i<=lena;i++)
for(j=1;j<=lenb;j++)
for(k=1;k<=lenc;k++)
{
if(a[i]==b[j]&&b[j]==c[k]) f[i][j][k]=a[i];
for(int x=max(0,i-7);x<i;x++)
for(int y=max(0,j-7);y<j;y++)
for(int z=max(0,k-7);z<k;z++)
if(f[i][j][k].size()<=f[x][y][z].size()+1)
f[i][j][k]=f[x][y][z]+a[i];
if(ans.size()<=f[i][j][k].size())
ans=f[i][j][k];
}
cout<<ans<<endl;
return 0;
}
- 运行结果与分析