人工智能(pytorch)搭建模型13-pytorch搭建RBM(受限玻尔兹曼机)模型，调通模型的训练与测试

大家好，我是微学AI，今天给大家介绍一下人工智能(pytorch)搭建模型13-pytorch搭建RBM(受限玻尔兹曼机)模型，调通模型的训练与测试。RBM(受限玻尔兹曼机)可以在没有人工标注的情况下对数据进行学习。其原理类似于我们人类学习的过程，即通过观察、感知和记忆不同事物的特点，从而形成对这些事物的认知模型。本文将介绍RBM（受限玻尔兹曼机）模型的原理，并使用PyTorch框架实现一个简单的RBM模型。我们将介绍如何构建模型，加载样例数据进行训练，以及在训练完成后进行测试。

文章目录结构：

RBM模型简介
RBM模型原理
使用PyTorch搭建RBM模型
数据样例及加载
模型训练
模型测试
总结

1. RBM模型简介

受限玻尔兹曼机（RBM）是一种生成式随机神经网络，广泛应用于图像识别、语音识别、推荐系统等领域。RBM能够学习到数据的潜在表示，是深度学习的重要组成部分。

RBM 由一些可见变量和一些隐藏变量组成。它的基本思想是用一个二分图表示这些变量之间的关系。可见变量与隐藏变量之间没有边相连，而可见变量与其他可见变量、隐藏变量与其他隐藏变量之间都存在边相连。这种二分图结构使得 RBM 可以很好地对输入数据进行建模。

在训练阶段，RBM 的目标是学习一个能量模型，使得训练数据的概率最大化。为了实现这个目标，通常使用下降梯度的方法来最小化负对数似然函数（Negative Log-Likelihood，NLL），从而得到隐含层向量和可见层向量之间的权重和偏置值。当模型参数学习完成后，我们可以使用 RMB 对新的数据进行生成、降噪等处理。

RBM 能够有效地应用于很多领域，例如语音识别、图像处理、自然语言处理等。同时，它还是其他深度学习模型的基础，例如深度信念网络（Deep Belief Network，DBN）和深度玻尔兹曼机（Deep Boltzmann Machine，DBM）等。
在这里插入图片描述

2. RBM模型原理

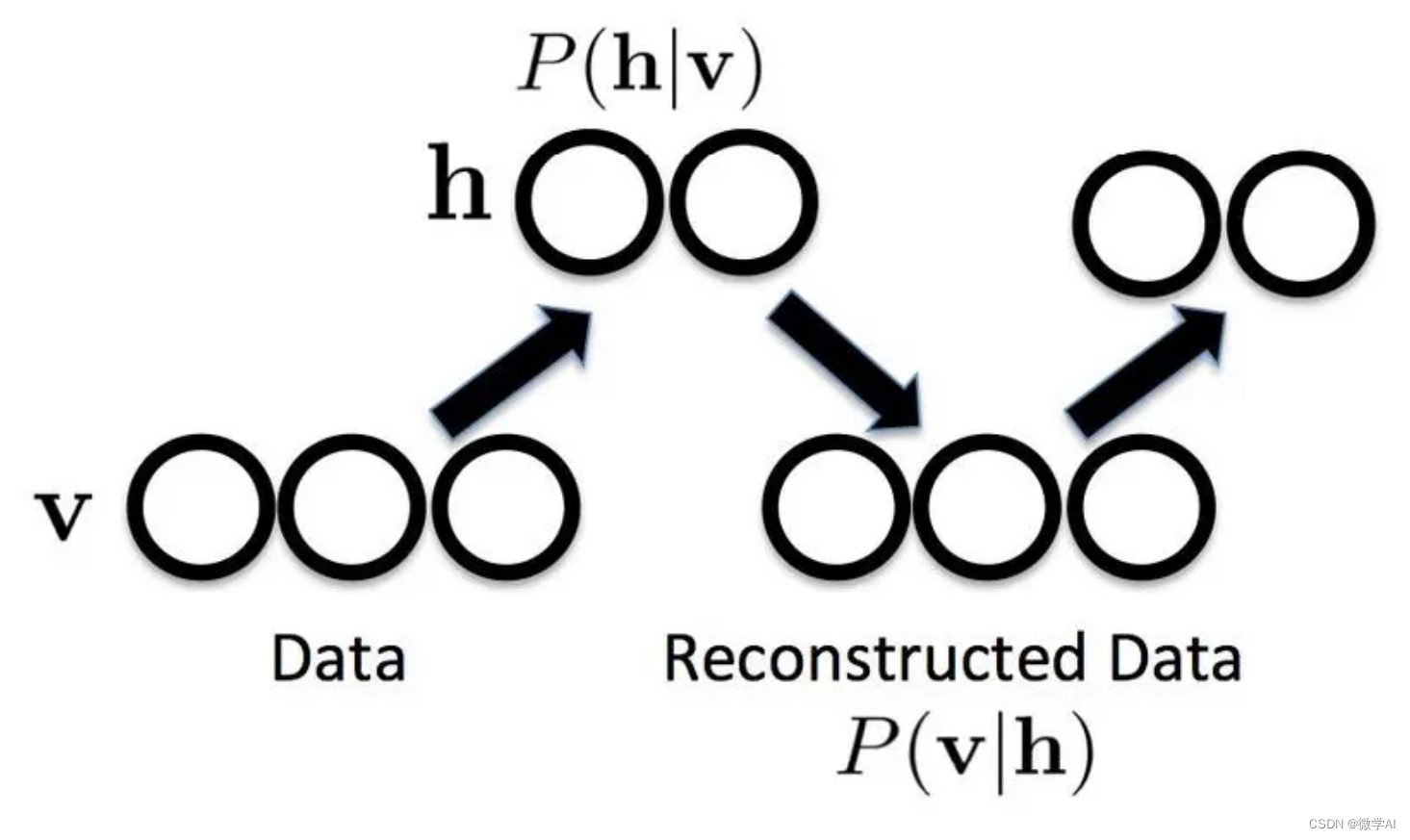
RBM是一个二部图模型，包括可见层（visible layer）和隐藏层（hidden layer），两层之间存在连接权重。可见层负责接收原始数据，隐藏层负责提取特征。与其他神经网络不同，RBM没有输出层，其学习过程是无监督的。

RBM的训练过程包括正向传播（从可见层到隐藏层）和反向传播（从隐藏层到可见层）。训练目标是最大化数据的对数似然，通过对比散度（Contrastive Divergence，简称CD）算法进行权重更新。

受限玻尔兹曼机（RBM）是一种用于无监督学习的概率生成模型。它由可见层和隐藏层组成，通过学习数据的分布来捕捉数据中的特征。

RBM的数学原理可以通过以下公式表示：

可见层的状态：
$\frac{1}{Z} \sum_h e^{-E(v,h)}$

隐藏层的状态：
$\frac{1}{Z} \sum_v e^{-E(v,h)}$

其中，$ E(v,h) $ 是能量函数，$ Z $是归一化常数。

RBM的学习过程主要包括两个步骤：正向传播和反向传播。

正向传播（Positive Phase）：

在正向传播中，给定一个可见层的输入样本，通过计算隐藏层的激活概率来更新隐藏层的状态。

$P(h_j=1|v) = \sigma\left(\sum_{i=1}^{n_v} w_{ij} v_i + c_j\right)$

其中，$ \sigma(x) $是sigmoid函数。

反向传播（Negative Phase）：

在反向传播中，通过计算可见层的激活概率来更新可见层和隐藏层的状态。

$P(v_i=1|h) = \sigma\left(\sum_{j=1}^{n_h} w_{ij} h_j + b_i\right)$

通过交替进行正向传播和反向传播，RBM可以学习到数据的分布，并用于生成新的样本。

3. 使用PyTorch搭建RBM模型

首先导入需要的库：

import torch
import torch.nn as nn
import torch.optim as optim
import numpy as np

接下来定义RBM模型：

class RBM(nn.Module):
    def __init__(self, visible_dim, hidden_dim, k=1):
        super(RBM, self).__init__()
        self.visible_dim = visible_dim
        self.hidden_dim = hidden_dim
        self.k = k
        self.W = nn.Parameter(torch.randn(visible_dim, hidden_dim) * 0.01)
        self.visible_bias = nn.Parameter(torch.zeros(visible_dim))
        self.hidden_bias = nn.Parameter(torch.zeros(hidden_dim))

    def sample_hidden(self, visible_probs):
        hidden_probs = torch.sigmoid(torch.matmul(visible_probs, self.W) + self.hidden_bias)
        return torch.bernoulli(hidden_probs)

    def sample_visible(self, hidden_probs):
        visible_probs = torch.sigmoid(torch.matmul(hidden_probs, self.W.t()) + self.visible_bias)
        return torch.bernoulli(visible_probs)

    def contrastive_divergence(self, visible):
        v0 = visible
        h0 = self.sample_hidden(v0)
        v_k = v0.clone()
        for _ in range(self.k):
            h_k = self.sample_hidden(v_k)
            v_k = self.sample_visible(h_k)
        return v0, h0, v_k

    def forward(self, visible):
        v0, h0, v_k = self.contrastive_divergence(visible)
        positive_association = torch.matmul(v0.t(), h0)
        negative_association = torch.matmul(v_k.t(), self.sample_hidden(v_k))
        return positive_association - negative_association

4. 数据样例及加载

为了简化问题，我们使用二值化的MNIST数据集作为示例。数据集包含手写数字0-9的灰度图像，每个图像的大小为28x28。我们需要将数据转换为可见层的形式。

from torchvision import datasets, transforms

def bernoulli(x):
    return torch.bernoulli(x)

transform = transforms.Compose([
    transforms.ToTensor(),
    transforms.Lambda(bernoulli)
])

mnist_train = datasets.MNIST(root='./data', train=True, download=True, transform=transform)
mnist_test = datasets.MNIST(root='./data', train=False, download=True, transform=transform)

train_loader = torch.utils.data.DataLoader(mnist_train, batch_size=5, shuffle=True, num_workers=2)
test_loader = torch.utils.data.DataLoader(mnist_test, batch_size=5, shuffle=False, num_workers=2)

5. 模型训练

接下来，我们将训练RBM模型。设置超参数，实例化RBM模型，然后使用随机梯度下降（SGD）优化器进行训练。SGD 是一种常用的优化算法，其基本思想是在每个迭代步骤中，通过计算当前样本的梯度来更新模型参数，以逐步寻找最小化损失函数的全局最优解。

visible_dim = 28 * 28
hidden_dim = 128
k = 1
learning_rate = 0.01
epochs = 10

rbm = RBM(visible_dim, hidden_dim, k)
optimizer = optim.SGD(rbm.parameters(), lr=learning_rate)

for epoch in range(epochs):
    train_loss = 0
    for i, (data, _) in enumerate(train_loader):
        data = data.view(-1, visible_dim)
        optimizer.zero_grad()
        delta_W = rbm(data)
        loss = -torch.mean(delta_W)
        loss.backward()
        optimizer.step()
        train_loss += loss.item()
    print(f"Epoch {epoch + 1}/{epochs}, Loss: {train_loss / (i + 1)}")

6. 模型测试

在模型训练完成后，我们可以将其应用于实际任务，如特征提取、分类等。这里我们简单地展示如何使用训练好的RBM模型重构测试数据。

import matplotlib.pyplot as plt

def display_reconstruction(rbm, test_loader, num_images=5):
    _, (test_data, _) = next(enumerate(test_loader))
    test_data = test_data[:num_images].view(-1, visible_dim)
    v0, _, v_k = rbm.contrastive_divergence(test_data)

    fig, axes = plt.subplots(nrows=2, ncols=num_images, figsize=(10, 4))
    for i in range(num_images):
        axes[0, i].imshow(v0[i].view(28, 28).detach().numpy(), cmap='gray')
        axes[1, i].imshow(v_k[i].view(28, 28).detach().numpy(), cmap='gray')
        axes[0, i].axis('off')
        axes[1, i].axis('off')
    plt.show()

display_reconstruction(rbm, test_loader)

运行结果：

Epoch 1/10, Loss: 0.927296216373558
Epoch 2/10, Loss: 0.9289948132250097
Epoch 3/10, Loss: 0.9284022589268146
Epoch 4/10, Loss: 0.9277208608952198
Epoch 5/10, Loss: 0.9270475412525021
Epoch 6/10, Loss: 0.9267477485059382
Epoch 7/10, Loss: 0.9266238975358176
Epoch 8/10, Loss: 0.9262511341960042
Epoch 9/10, Loss: 0.9246195605427593
Epoch 10/10, Loss: 0.9238044374525011