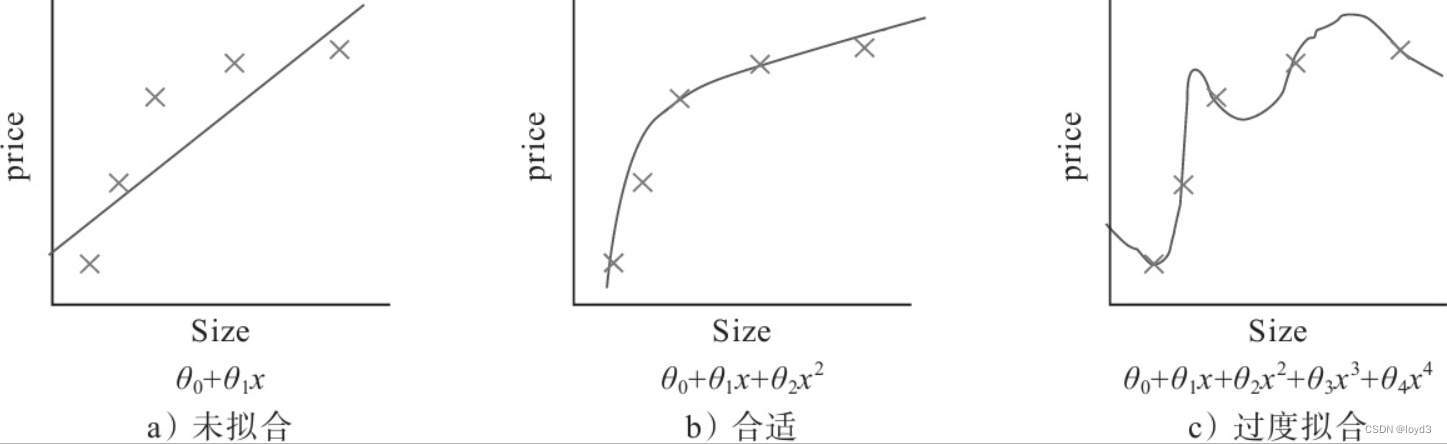
机器学习的问题中，过拟合是一个很常见的问题。过拟合指的是只能拟合训练数据，但不能很好地拟合不包含在训练数据中的其他数据的状态。机器学习的目标是提高泛化能力，即便是没有包含在训练数据里的未观测数据也希望模型可以进行正确的识别。

发生过拟合的原因，主要有以下两个：

• 模型拥有大量参数、表现力强。
• 训练数据少。

那么如何来抑制过拟合
正则化是有效方法之一，它不仅可以有效降低高方差，还有利于降低偏差。何为正则化？在机器学习中，很多被显式地用来减少测试误差的策略，统称为正则化。正则化旨在减少泛化误差而不是训练误差。
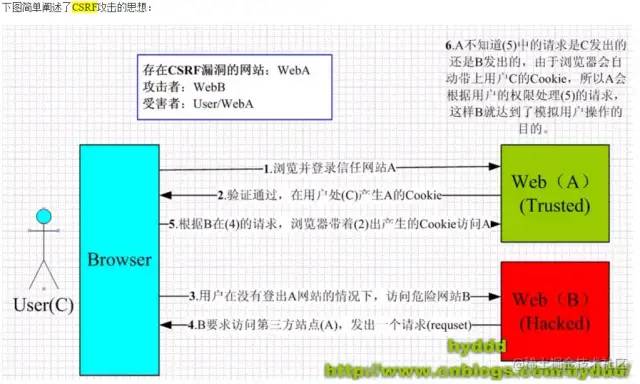
下面是几张与正则化相关的图片

权值衰减
权值衰减是一直以来经常被使用的一种抑制过拟合的方法。该方法通过在学习的过程中对大的权重进行惩罚，来抑制过拟合。很多过拟合原本就是因为权重参数取值过大才发生的。

复习一下，神经网络的学习目的是减小损失函数的值。这时，例如为损失函数加上权重的平方范数(L2范数)。这样一来，就可以抑制权重变大。
实现L2正则化时，Ω(w)的表达式为：

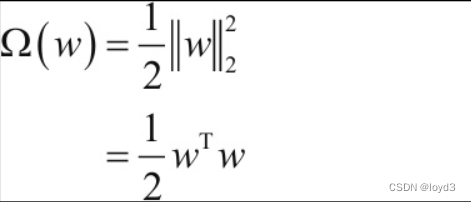
用符号表示的话，如果将权重记为，L2范数的权值衰减就是$\frac{1}{2}$ $\lambda$$W^2$，然后将这个$\frac{1}{2}$ $\lambda$$W^2$加到损失函数上。这里，$\lambda$是控制正则化强度的超参数。设置得越大，对大的权重施加的惩罚就越重。此外，开头的二分之一是用于将$\frac{1}{2}$ $\lambda$$W^2$的求导结果变成
$\lambda$$W^2$对于所有权重，权值衰减方法都会为损失函数加上$\frac{1}{2}$ $\lambda$$W^2$。因此，在求权重梯度的计算中，要为之前的误差反向传播法的结果加上正则化项的导数$\lambda$$W^2$
L2范数相当于各个元素的平方和

权值衰减的实现代码如下：

def loss(self, x, t):
    y = self.predict(x)

    weight_decay = 0
    for idx in range(1, self.hidden_layer_num + 2):
        W = self.params['W' + str(idx)]
        weight_decay += 0.5 * self.weight_decay_lambda * np.sum(W ** 2)

    return self.last_layer.forward(y, t) + weight_decay

实验代码最核心的部分是MultiLayerNet类添加了weight_decay_lambda参数，代码如下：

network = MultiLayerNet(input_size=784, hidden_size_list=[100, 100, 100, 100, 100, 100], output_size=10,
                        weight_decay_lambda=weight_decay_lambda)

其他部分和其他实验代码相差不大
得到的结果如下：

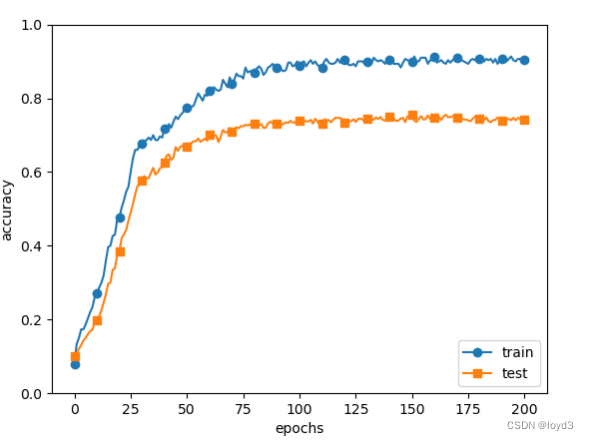
虽然训练数据的识别精度和测试数据的识别精度之间有差距，但是与没有使用权值衰减的结果相比，差距变小了。这说明过拟合受到了抑制。此外，还要注意，训练数据的识别精度没有达到100%

Dropout
Dropout是一种在学习的过程中随机删除神经元的方法。训练时，随机选出隐藏层的神经元，然后将其删除。被删除的神经元不再进行信号的传递。
训练时，每传递一次数据，就会随机选择要删除的神经元然后，测试时，虽然会传递所有的神经元信号，但是对于各个神经元的输出要乘上训练时的删除比例后再输出。

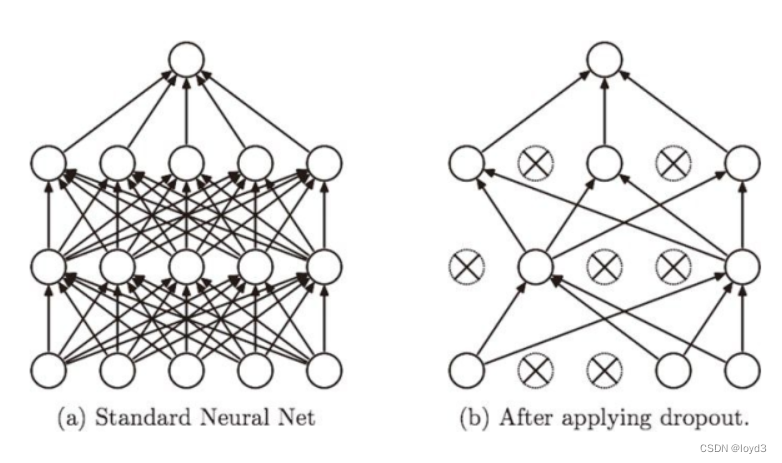
关于Dropout的实现，可以参考Chainer中的实现

class Dropout:
	def __init__(self,dropout_ratio=0.5):
		self.dropout_ratio = dropout_ratio
		self.mask = None

	def forward(self, x, train_flg = True):
		if train_flg:
			self.mask = np.random.rand(*x.shape) > self.dropout_ratio
			return x * self.mask
		else:
			return x * (1.0 - self.dropout_ratio)

	def backward(self, dout):
		return dout * self.mask

这里的要点是，每次正向传播时，self.mask中都会以False的形式保存删除的神经元。setf.mask会随机生成和x形状同的数组，并将值比dropout_ratio大的元素设为True。反向传播时的行为和ReLU相同。也就是说正向传播时传递了信号的神经元，反向传播时接原样传递信号；正向传播时没有传递信号的神经元，反向传播时信号将停在那里。

现在，我们使用MNIST数据集进行验证，代码如下：

# 省略import代码

(x_train, t_train), (x_test, t_test) = load_mnist(normalize=True)

# 为了再现过拟合，减少学习数据
x_train = x_train[:300]
t_train = t_train[:300]

# 设定是否使用Dropuout，以及比例 ========================
use_dropout = True  # 不使用Dropout的情况下为False
dropout_ratio = 0.2
# ====================================================

# 在MultiLayerNetExtend中设置是否使用Dropuout
network = MultiLayerNetExtend(input_size=784, hidden_size_list=[100, 100, 100, 100, 100, 100],output_size=10, 
use_dropout=use_dropout, dropout_ration=dropout_ratio)

trainer = Trainer(network, x_train, t_train, x_test, t_test,
                  epochs=301, mini_batch_size=100,
                  optimizer='sgd', optimizer_param={'lr': 0.01}, verbose=True)
trainer.train()

train_acc_list, test_acc_list = trainer.train_acc_list, trainer.test_acc_list

# 省略绘图代码

测试代码中使用了Trainer类来简化实现

下面是测试的结果：

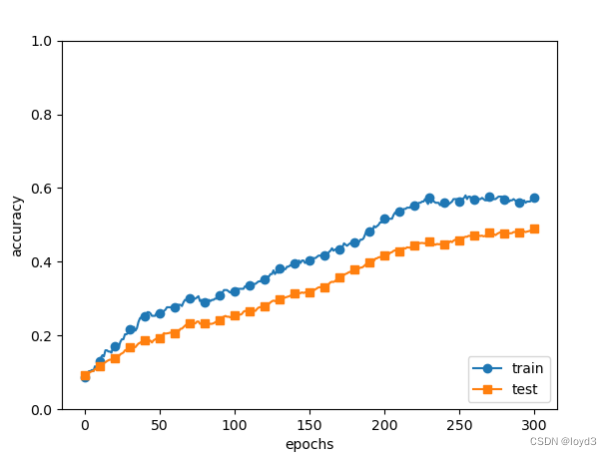
和没有使用Dropout的相比

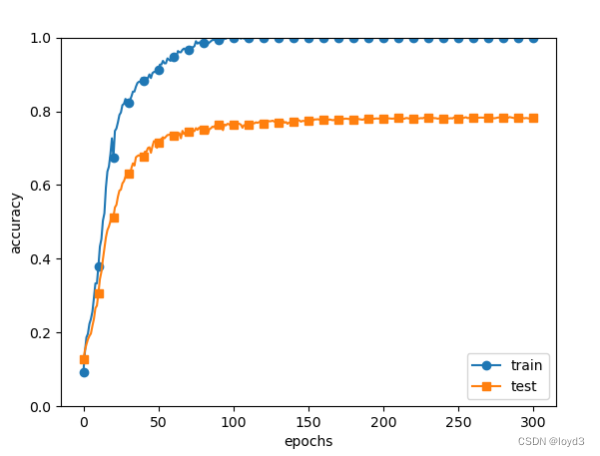
通过使用Dropout，训练数据和测试数据的识别精度的差变小了。并且，训练数据也没有到达100%的识别精度。像这样，通过使Dropout，即便是表现力强的网络，也可以抑制过拟合。

可以将Dropout理解为，通过在学习过程中随机删除神经元，从而每一次都让不同的模型进行学习。并且，推理时，通过对神经元的输出乘以删除比例(比如，0.5等)，可以取得模型的平均值。也就是说，可以理解成Dropout将集成学习的效果(模拟地)通过一个网络实现了。

如何或何时使用Dropout呢？以下是使用的一般原则：

1. 通常**丢弃率控制在20%～50%**比较好，可以从20%开始尝试。如果比例太低则起不到效果，比例太高则会导致模型的欠学习。
2. 在大的网络模型上应用。当Dropout用在较大的网络模型时，更有可能得到效果的提升，模型有更多的机会学习到多种独立的表征。
3. 在输入层和隐藏层都使用Dropout。对于不同的层，设置的keep_prob也不同，一般来说，神经元较少的层，会设keep_prob为1.0或接近于1.0的数；神经元多的层，则会将keep_prob设置的较小，如0.5或更小。
4. 增加学习速率和冲量。把学习速率扩大10～100倍，冲量值调高到0.9～0.99。
5. 限制网络模型的权重。大的学习速率往往导致大的权重值。对网络的权重值做最大范数的正则化，可以提升模型性能。