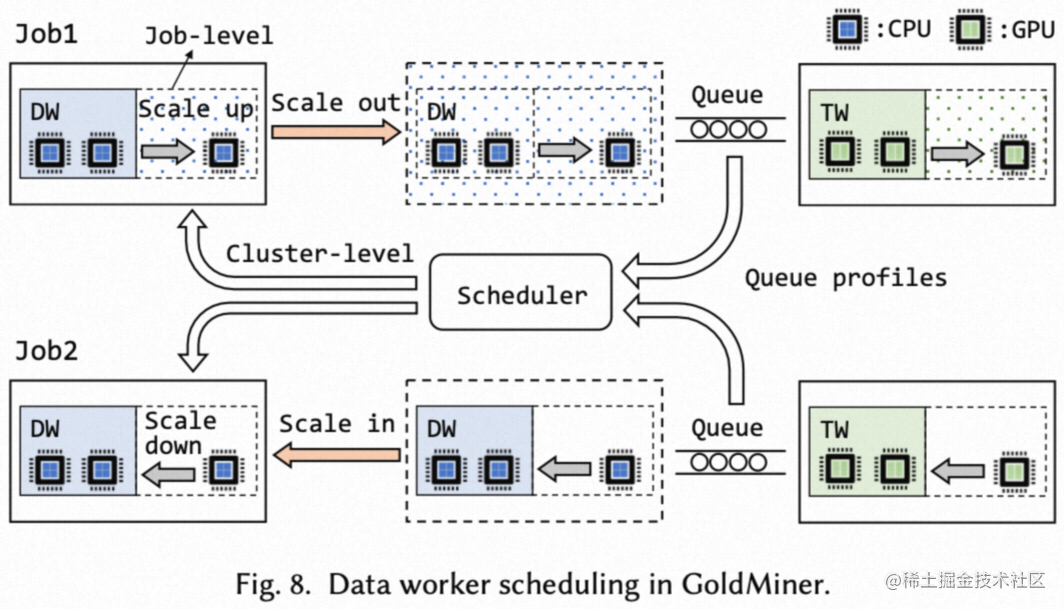
上述考虑的问题，我们会得到一个式子，即：Y=θ1·X1+θ2·X2。但该线性公式没办法拟合所有的数据点，如下图。

       这里“θ0”作为偏置项，在二维平面里，即为截距。因此，上述公式“Y=θ1·X1+θ2·X2”即可修改为“Y=θ0+θ1·X1+θ2·X2”，将常数项“θ0”添加一个“X0”，即可用矩阵形式表示该公式。这里“X0”为常数“1”，没有实际含义。

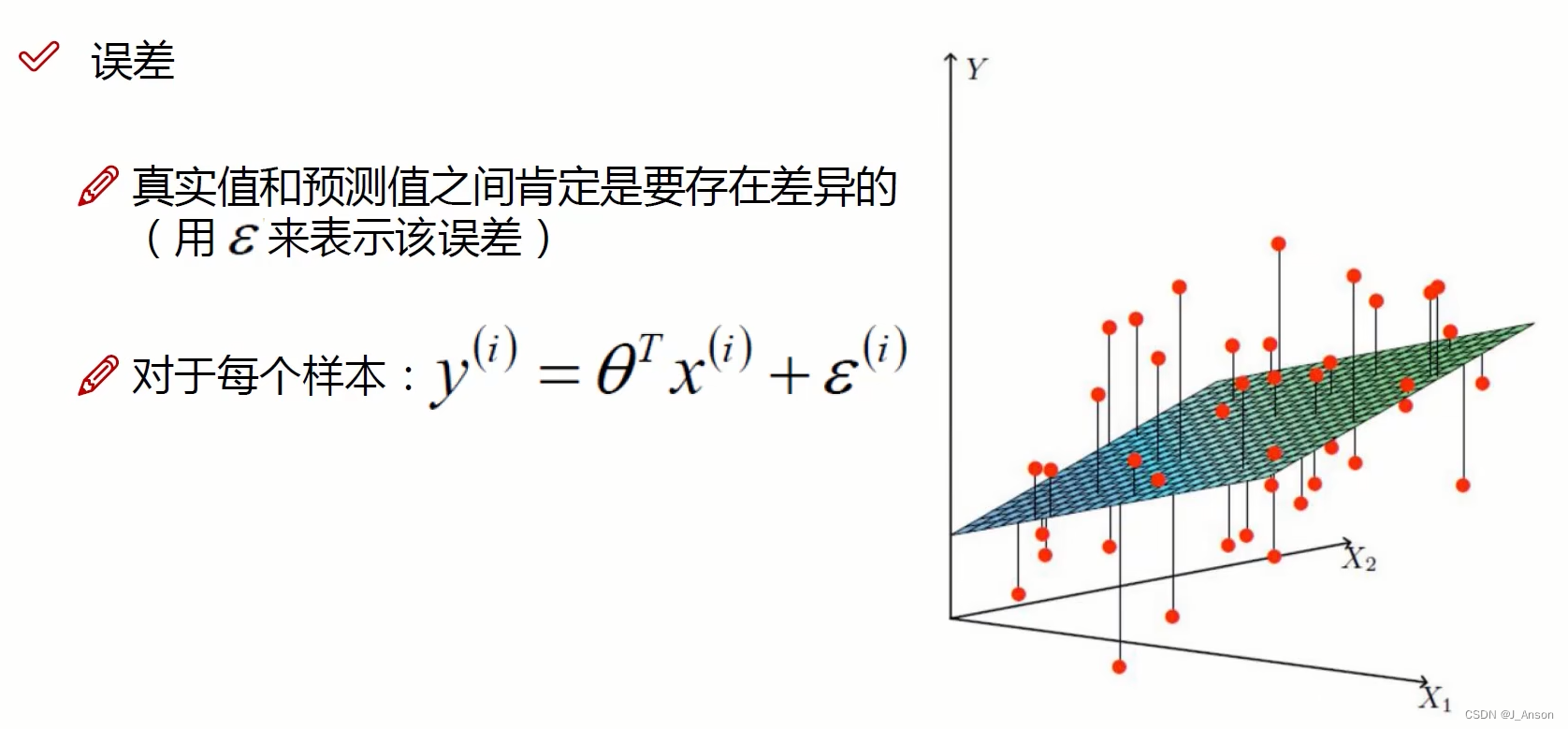
       由于误差的存在，因此上述公式，Y(i)为真实值，θT·X（i）为预测值，E(i)为误差，我们希望误差项越小越好，即损失函数的结果越小越好。

       这里的误差，每个样本的误差值之间互不干涉，互相独立；同分布针对数据集来说，即来自同一处的数据，如同一个银行的数据。

       误差符合正态分布（高斯分布），但实际数据的分布不会完美符合正态分布，但这不影响误差整体符合这类规律。

       将（1）带入（2）的所得，即为X(i)和θ的组合，成为真实值Y(i)的可能性。我们希望可能性越大越好。

       这里可以转换成加法计算的原因是：我们并不关心L(θ)的极值是多少，我们只关心使得L(θ)取得极值的极值点是多少。类比一元二次方程，我们知道极值点X=？并不会受到两边同乘或者同除A的影响（仅为影响极值的大小）。因此，我们即可对误差进行化简。

       从而求解函数。这里X，θ，Y均为矩阵。这里，XT·X（矩阵X的转置·矩阵X）的目的，是为了将X转换为对称阵（方阵），X和Y均为已知量。

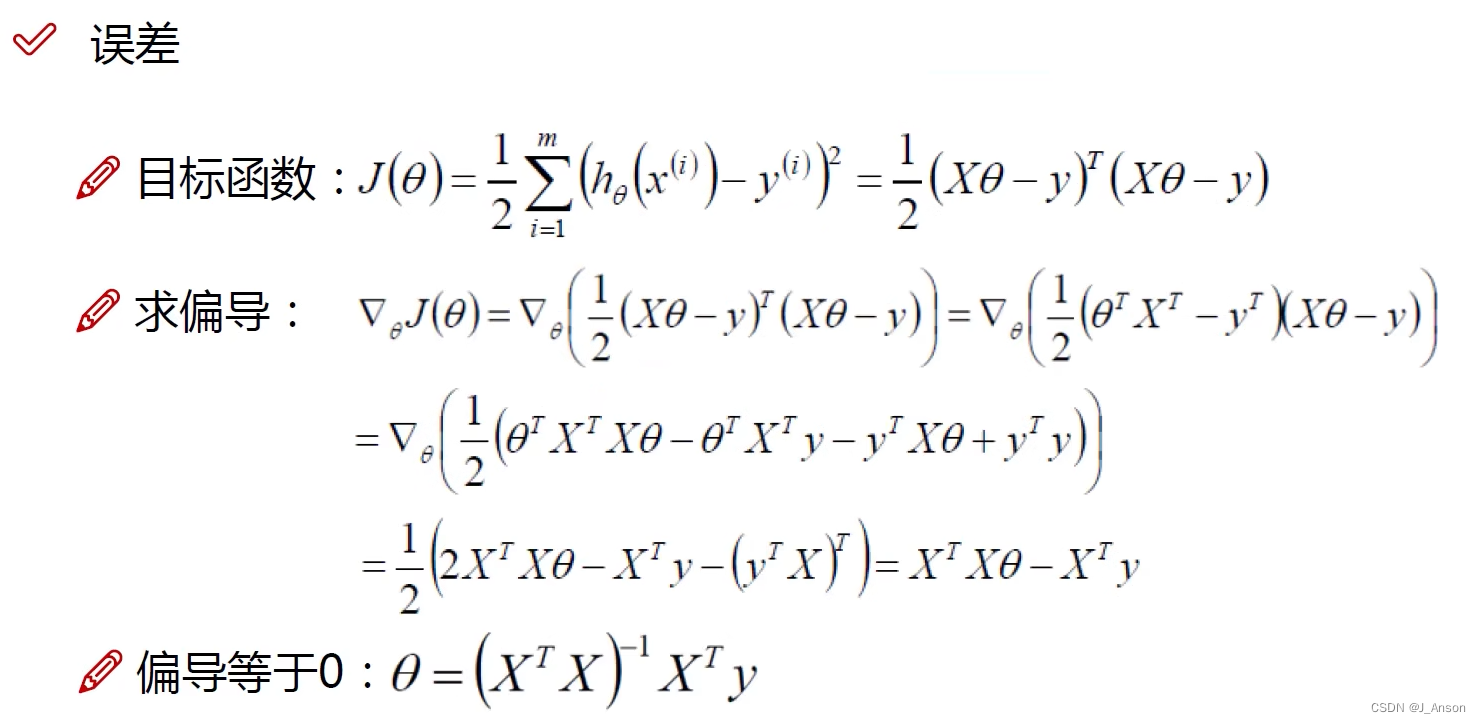
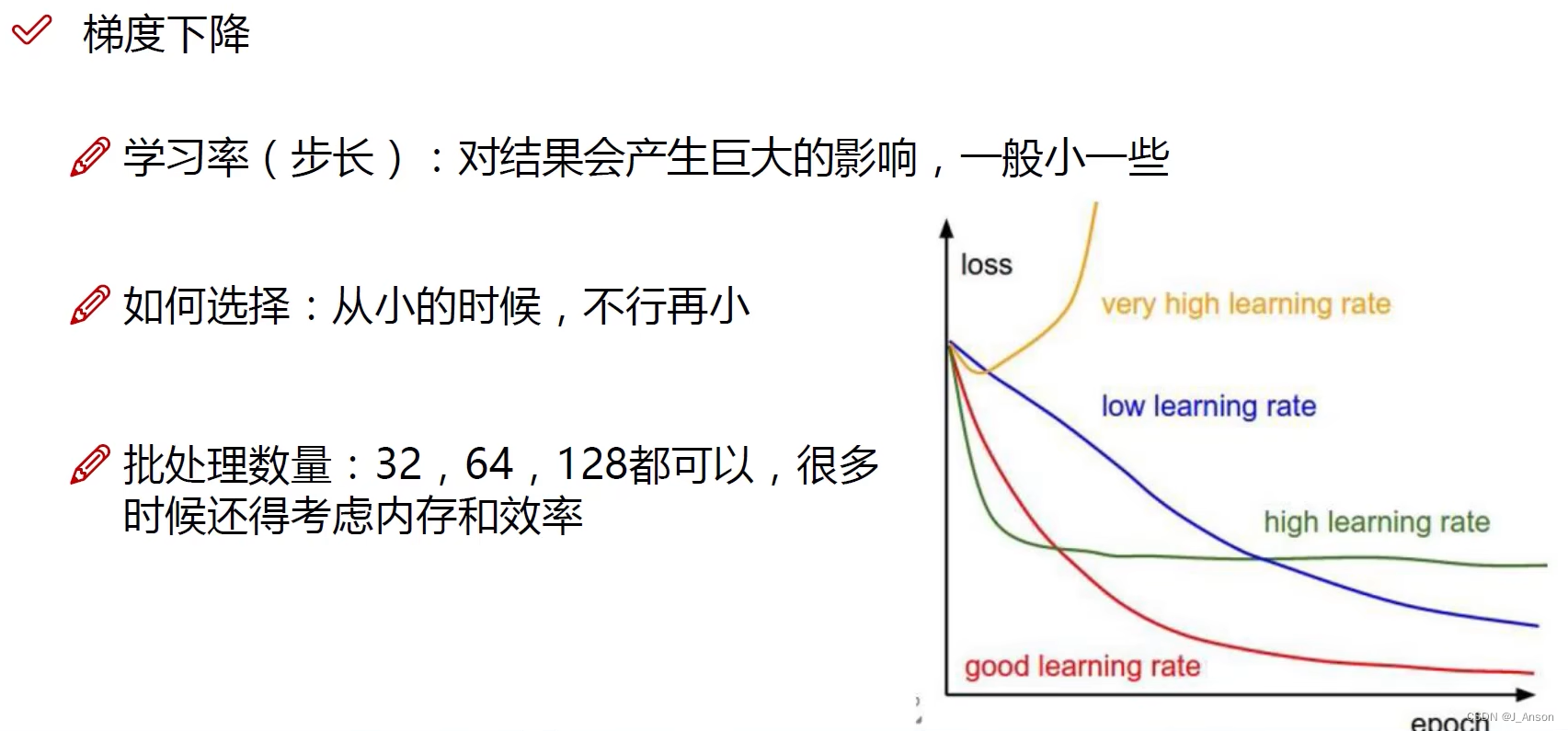
       上述虽然可以直接得到结果，但针对多数情况，我们需要学习的过程，梯度下降即为其中一种学习的方法。

       这里，由于数据样本X0和X1之间是独立的，因此优化的过程，是分别对θ0和θ1进行 优化。

       梯度方向是上升最快的方向，因此，这里的偏导结果应该取反，再加上原来θj的位置，即为更新后的位置。

       考虑数据样本的大小，批量梯度下降，每次都需要对所有样本数据求偏导在平均，因此计算量很大，梯度下降速度在数据集大的情况下慢。

       随机梯度下降由于每次找的样本是随机的，不一定是下降速度最快的方向，结果不可控。

       小批量梯度下降，综合了上述两种的优点，每次更新选区一小部分数据样本来计算（常用），受选择样本大小（batch包含样本数量的多少）的影响。

       上面公式的α即下面的学习率。