1. 前情回顾

归并排序是一个全新的排序
它不是对任意排序的优化和改进
它自成一派,并且效率非常可观
要想掌握归并的非递归版本
就要先理解归并递归版实现
详情可以跳转:归并初阶篇

掌握了非递归版将是面试时
你和别人拉开差距的重要一环
大学生特种兵,开卷!

在这里插入图片描述

2. 归并非递归基本思路

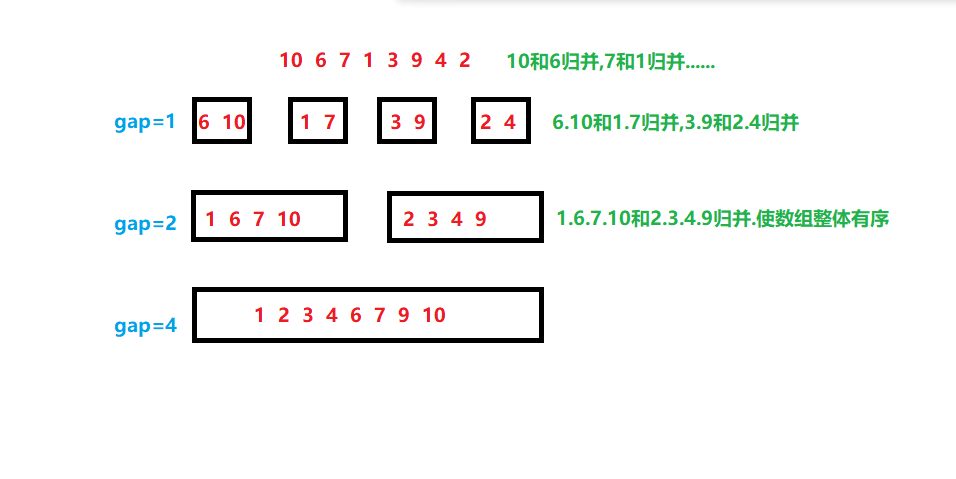
我们先定义一个无序数组:

int a[]={10,6,7,1,3,9,4,2};

对于当前数组.

我们需要做的是:

第一次循环:

将10和6这一组,7和1这一组
3和9这一组,4和2这一组归并排序
使这四组的各两个数变为有序

第二次循环:

6.10和1.7一组,3.9和2.4一组
进行归并排序,使这两组的各
四个数字都变为有序

第三次循环:

1.6.7.10和2.3.4.9一组
进行归并排序,使数组整体有序

画图理解:

在这里插入图片描述

3. 对于循环的(大/小)框架的思考

对于大框架的思考:

先来找找规律:

八个元素需要归并三次
四个元素需要归并两次
十六个元素需要归并四次

归并循环的次数K和数组元素个数n
的关系是:

2 ^ K = n

所以我们可以这样设计最外层循环:

int gap=1;
while(gap<n)
{
	//...
	gap* = 2;
}

对于小框架的思考:

循环第一次

区间 [0,0] 和区间 [1,1] 归并
区间 [2,2] 和区间 [3,3] 归并

循环第二次

区间 [0,1] 和区间 [2,3]归并
区间 [4,5] 和区间 [6,7]归并

循环第三次

区间 [0,3] 和区间 [4,7] 归并
归并结束,数组整体有序.

我们根据画图中的gap来思考:
gap从1开始,每归并一次便扩大两倍
每次循环的区间可以这样定义:

A组: [ i , i + gap - 1]
B组: [ i + gap , i + 2*gap - 1]

所以我们可以这样设计内层循环:

for(int i=0;i<n;i+=2*gap)
{
	//...
}

4. 归并排序非递归代码实现

有了前面做铺垫,直接上硬菜:

//归并排序(非递归)偶数没问题,奇数还需要改正
void MergeSortNonRE(int* a, int n)
{
	int* tmp = (int*)malloc(sizeof(int) * n);
	if (tmp == NULL)
	{
		printf("动态开辟失败");
		exit(-1);
	}
	int gap = 1;
	while (gap < n)
	{
		for (int i = 0; i < n; i = i + 2 * gap)
		{
			int begin1 = i;
			int end1 = i + gap - 1;
			int begin2 = i + gap;
			int end2 = i + 2 * gap - 1;
			int index = i;
			while (begin1 <= end1 && begin2 <= end2)
			{
				if (a[begin1] < a[begin2])
				{
					tmp[index++] = a[begin1++];
				}
				else
				{
					tmp[index++] = a[begin2++];
				}
			}
			while (begin1 <= end1)
			{
				tmp[index++] = a[begin1++];
			}
			while (begin2 <= end2)
			{
				tmp[index++] = a[begin2++];
			}
		}
		for (int i = 0; i < n; i++)
		{
			a[i] = tmp[i];
		}
		gap = gap * 2;
	}

	free(tmp);
	tmp = NULL;
}

注意:只有大小框架的设计是本节内容
归并排序具体实现(也就是后面的代码)
具体可以参考:归并排序初阶篇

5. 特殊情况下对代码的优化

对元素个数为偶数的思考:

上面的情况用到的用例的
数组元素个数都是偶数个
所以可以两两匹配,归并不会出错

先定义一个奇数个元素的数组:

int a[]={10,6,7,1,3,9,4,2,5};

对元素个数为奇数的思考:

而当数组元素个数是奇数个时
归并完4.2后.归并5和5后面的元素
然而5后面的元素不存在,或者说越界了
系统就会报错,因为有越界操作存在
这里需要优化代码解决这个问题

优化后的代码:

//归并排序(非递归完全版)
void MergeSortNonR(int* a, int n)
{
	int* tmp = (int*)malloc(sizeof(int) * n);
	if (tmp == NULL)
	{
		printf("动态开辟失败");
		exit(-1);
	}
	int gap = 1;
	while (gap < n)
	{
		for (int i = 0; i < n; i = i + 2 * gap)
		{
			int begin1 = i;
			int end1 = i + gap - 1;
			int begin2 = i + gap;
			int end2 = i + 2 * gap - 1;
			
			//处理特殊的越界情况
			// end1 越界，[begin2,end2]不存在
			if (end1 >= n)
			{
				end1 = n - 1;
			}

			//[begin1,end1]存在 [begin2,end2]不存在
			if (begin2 >= n)
			{
				begin2 = n;
				end2 = n - 1;
			}

			if (end2 >= n)
			{
				end2 = n - 1;
			}

			int index = i;
			while (begin1 <= end1 && begin2 <= end2)
			{
				if (a[begin1] < a[begin2])
				{
					tmp[index++] = a[begin1++];
				}
				else
				{
					tmp[index++] = a[begin2++];
				}
			}
			while (begin1 <= end1)
			{
				tmp[index++] = a[begin1++];
			}
			while (begin2 <= end2)
			{
				tmp[index++] = a[begin2++];
			}
		}
		for (int i = 0; i < n; i++)
		{
			a[i] = tmp[i];
		}
		gap = gap * 2;
	}

	free(tmp);
	tmp = NULL;
}