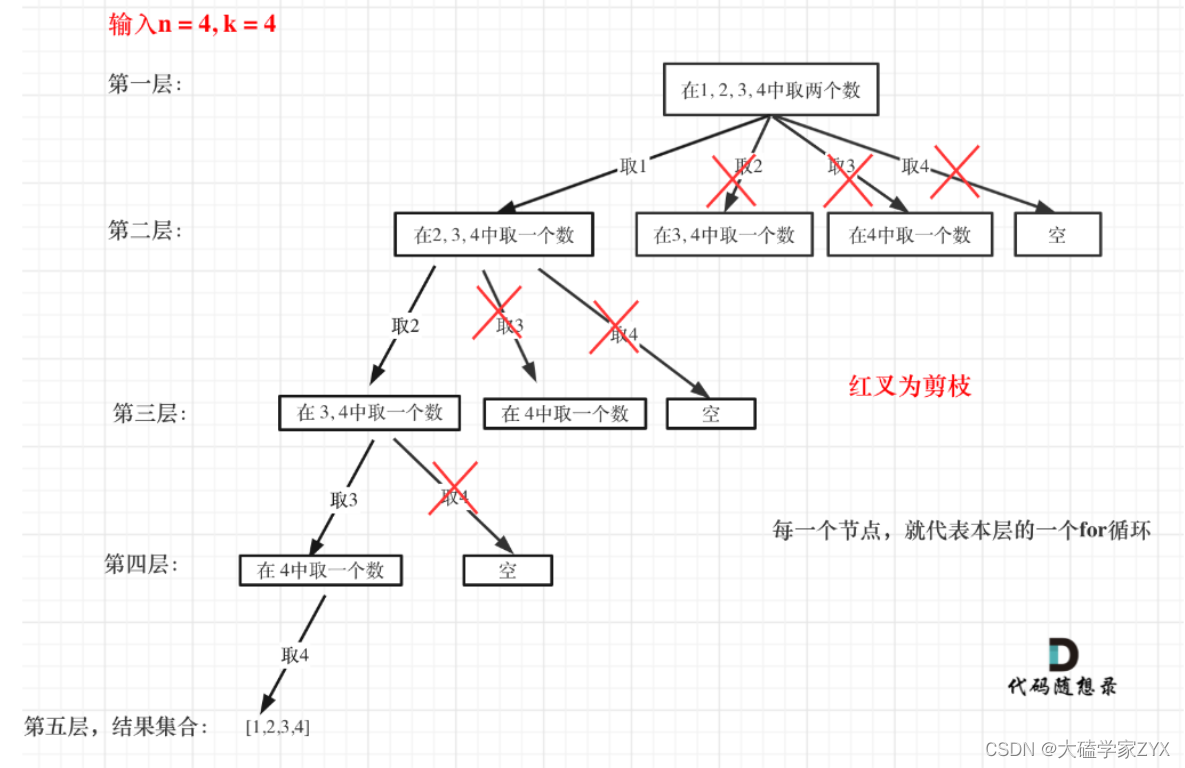
3.分治法

3.1递归

递归是指子程序（或函数）直接调用自己或通过一系列调用语句间接调用自己，是一种描述问题和解决问题的常用方法。使用递归技术往往使函数的定义和算法的描述简洁且易千理解。
递归有两个基本要素：边界条件，即确定递归到何时终止，也称为递归出口；递归模式，即大问题是如何分解为小问题的，也称为递归体。
阶乘函数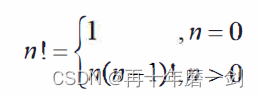：在这里插入图片描述

阶乘函数的自变量n的定义域是非负整数。递归式的第一式给出了这个函数的一个初始值，是递归的边界条件。递归式的第二式是用较小自变量的函数值来表示较大自变量的函数值的方式来定义n的阶乘，是递归体。

3.2分治法的基本思想

分治与递归就像一对李生兄弟，经常同时应用于算法设计之中，并由此产生许多高效的算法。分治法的设计思想是将一个难以直接解决的大问题分解成一些规模较小的相同问题，以便各个击破，分而治之。如果规模为n的问题可分解成K个子问题， 1<k≤n, 这些子问题互相独立且与原问题相同。分治法产生的子问题往往是原问题的较小模式，这就为递归技术提供了方便。
一般来说，分治算法在每一层递归上都有3个步骤。
(1) 分解。将原问题分解成一系列子问题。
(2) 求解。递归地求解各子问题。若子问题足够小，则直接求解。
(3) 合并。将子问题的解合并成原问题的解。

3.3 分治法的典型实例

3.3.1 归并排序算法

归并排序是成功应用分治法的一个完美的例子，其基本思想是将待排序元素分成大小大致相同的两个子序列，分别对这两个子序列进行排序，最终将排好序的子序列合并为所要求的序列。归并排序算法完全依照上述分治算法的3个步骤进行。
(1) 分解。将n个元素分成各含n/2个元素的子序列。
(2) 求解。用归并排序对两个子序列递归地排序。
(3) 合并。合并两个已经排好序的子序列以得到排序结果。

Java代码如下

public class MergeSort {
    public static void main(String[] args) {
        int[] arr = {54,87,56,36,12,7,35,27,48,98,67,72};
        sort(arr);
        System.out.println(Arrays.toString(arr));
    }
    static void sort(int[] arr) {
        sort(0, arr.length - 1, arr);
    }

    static void sort(int start, int end, int[] arr) {
        //递归终止条件
        if (start < end) {
            int mid = (start + end) / 2;
            sort(start, mid, arr);
            sort(mid + 1, end, arr);
            merge(start, mid, end, arr);
        } else {
            return; 
        }
    }

    static void merge(int start, int mid, int end, int[] arr) {
        int[] temp = new int[end - start + 1];
        int k = 0;
        int i = start;
        int j = mid + 1;
        while (i <= mid && j <= end) {
            if (arr[i] < arr[j]) {
                temp[k++] = arr[i++];
            }else {
                temp[k++] = arr[j++];
            }
        }
        //当i或j指针超出范围时
        while(i<=mid){
            temp[k++] = arr[i++];
        }
        while (j<=end){
            temp[k++] = arr[j++];
        }
        System.arraycopy(temp, 0, arr, start, end - start + 1);
    }
}

Merge显然可在O(n) 时间内完成，因此归并排序算法对n个元素进行排序所需的计算时间T(n)满足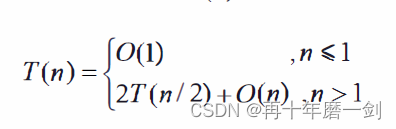：在这里插入图片描述用主方法解这个递归式得：T(n)=O(nlogn)

3.3.2 最大子段和问题

给定由n个整数（可能有负整数）组成的序列a₁,a₂,…,a_n，求该序列子段和的最大值。当序列中所有整数均为负整数时，其最大子段和为0。

java代码：

public class MaxSubSum {
    public static void main(String[] args) {
        int[] arr =  { -2, 1, -3, 4, -1, 2, 1, -5, 4 };
        System.out.println(maxSub(arr));
    }
    public static int maxSub(int[] arr) {
        return maxSub(arr, 0, arr.length - 1);
    }

    public static int maxSub(int[] arr, int left, int right) {
        if (left == right) {
            return arr[left];
        }
        int mid = left + (right - left) / 2 ;
        int leftMax = maxSub(arr, left, mid);
        int rightMax = maxSub(arr, mid + 1, right);
        int crossMax = maxCross(arr, left, right, mid);
        int max = Math.max(Math.max(leftMax, rightMax), crossMax);
        if(max >0){
            return max;
        }else {
            return 0;
        }
    }

    public static int maxCross(int[] arr, int left, int right, int mid) {
        int leftMax = Integer.MIN_VALUE;
        int rightMax = Integer.MIN_VALUE;
        int sum = 0;
        for (int i = mid; i >= left; i--) {
            sum += arr[i];
            leftMax = Math.max(leftMax, sum);
        }
        sum = 0;
        for (int i = mid + 1; i <= right; i++) {
            sum += arr[i];
            rightMax = Math.max(rightMax, sum);
        }
        return leftMax + rightMax;
    }
}

分析时间复杂度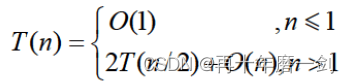：在这里插入图片描述