图神经网络的基本结构

图神经网络 (Graph Neural Network, GNN) 是一类用于处理图数据的深度学习模型。它可以对图的节点和边进行学习，适用于各种图结构的任务，如节点分类、链接预测、社区发现等。图神经网络的基本结构通常由以下两部分组成：

节点嵌入（Node Embedding）：将图中的每个节点映射为一个低维向量表示，通常使用一些线性变换、非线性激活函数和归一化等技术来实现。节点嵌入的目的是捕捉节点的特征和局部结构信息。
图卷积（Graph Convolution）：利用节点嵌入和图结构信息对节点特征进行更新，从而实现对整个图的表示学习。图卷积运算通常可以看作是一种基于局部邻域特征的聚合操作，同时考虑节点特征和局部拓扑结构信息。图卷积的主要目的是通过迭代更新节点嵌入从而实现对图结构的表示学习。

除了这两部分，图神经网络还可能包括其他一些模块，如注意力机制、池化层和分类器，用于更好地处理图数据的特点和复杂性。

需要注意的是，不同类型的图神经网络可能具有不同的节点嵌入和图卷积设计，例如，GCN使用拉普拉斯矩阵和傅里叶变换来进行图卷积，而GAT使用注意力机制来融合不同节点之间的信息。

图谱和图傅里叶变换

图谱是图的拉普拉斯矩阵的特征值。 具体来说，给定图G=(V,E)，其中V和E分别表示图G的节点集和边集，假设n表示节点数，图G的邻接矩阵A为一个n x n的矩阵，如果节点i,j之间有边相连，则A_ij=1，否则A_ij=0。图G的度矩阵为D=diag(d1, d2,…,dn)，其中di表示第i个节点在图中的度数（degree）。定义图的拉普拉斯矩阵 L = D - A，对其进行特征值分解：
在这里插入图片描述
其中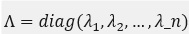，是按照特征值从小到大的顺序排列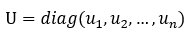，是对应的特征向量组成的正交矩阵。上述特征值集合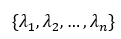即为图G的图谱。

图傅里叶变换（Graph Fourier Transform）是一种基于图信号处理的技术，类似于传统傅里叶变换，但适用于处理图数据。

在传统傅里叶变换中，将一个连续信号或离散信号通过傅里叶变换转换到频域中，这个频域展现了信号的频率特征，通常用于对信号进行滤波、去噪、压缩等操作。在图傅里叶变换中，类似的，我们把一个图信号（Graph Signal）通过傅里叶变换转换到图频域中，用于进行图结构分析、滤波等操作。

图傅里叶变换的计算方式和传统傅里叶变换存在显著的区别，它需要先将图转换为拉普拉斯矩阵（Laplacian Matrix），然后使用拉普拉斯矩阵对应的特征向量和特征值进行傅里叶变换。具体来说，假设有一个n个节点的图G，邻接矩阵为A，度数矩阵为D，则可以通过以下方式计算得到Laplacian Matrix：L = D - A。

将L的特征向量组成的矩阵记为U，特征值组成的向量记为λ，则可以得到图傅里叶变换：

f̂ = U^T * f，其中f是原始图信号，f̂是其在图傅里叶变换中的频域表示。

图傅里叶变换可以用于信号恢复、图形压缩、图像分析等多种应用，尤其适用于处理规则和不规则的图结构。

基于频谱域的GNN和基于空间域的GNN的比较

基于频谱域的GNN和基于空间域的GNN是目前两种主流的GNN模型。二者有着不同的特点和适用场景，下面进行简要比较：

原理

基于频谱域的GNN依靠图傅里叶变换将图信号（节点特征）转化到频域进行处理，节点特征的传播实质上是在频域上进行的。而基于空间域的GNN则通过聚合每个节点周围的邻居节点特征来更新当前节点的特征表示。

优缺点

基于频谱域的GNN具有较强的表达能力和稳定性，因为图傅里叶变换可以提供全局结构信息，能够捕捉图的本质特征。同时在一些平滑性较强的图上效果较好。但是基于频谱域的GNN存在运算量较大和具有较高的计算复杂度的问题。

基于空间域的GNN计算效率较高且易于实现，对于具有明显的局部特征的图（如社交网络、语义网络等）效果优秀。但是基于空间域的GNN难以处理全局结构信息和复杂图的边缘特征。

适用场景

基于频谱域的GNN适用于处理规则化或较平滑的图上，如Molecular Graphs（分子图结构）、Image Graphs（视觉任务图结构）等。而基于空间域的GNN适用于处理非规则化和复杂的图上，如Social Graphs（社交网络）、Textual Graphs（文本任务图结构）等。

总的来说，选择基于频谱域的GNN还是基于空间域的GNN需要根据具体应用场景和任务的特点来进行选择和评估。

图神经网络的任务需求和模型要求

任务需求

节点分类：给定一个图和部分节点的标签，预测剩余节点的标签。
链接预测：给定一个图，预测两个节点之间是否有边。
社区发现：给定一个图，把节点分为若干个社区。
图特征提取：从原始图像数据中提取出高层次的特征表示，用于后续的分类和识别。

模型要求

空间不变性：GNN应该对图中节点的排列没有偏见，即空间不变性。
局部性：对于每个节点，GNN 应该只考虑其邻居节点的信息，而不考虑整个图的信息，即局部性。
可复现性：GNN 应该能够对同一张图进行多次模型训练并得到相同的结果。
可扩展性：GNN 应该能够处理大规模的图数据，同时防止模型过拟合和欠拟合。
鲁棒性：GNN 应该能够处理缺失数据或噪声数据的情况，并保持稳定的性能。

为了满足上述要求，GNN 模型通常具有以下几个特征：

基于邻接矩阵的卷积运算，在每个节点上进行卷积、池化和全连接操作。
节点表示的更新方式通常基于节点本身的特征以及它的邻居节点的特征，用来表示节点在整个图中的上下文信息。
GNN 通常使用梯度下降算法进行训练，同时结合正则化、Dropout 等技术来避免模型过拟合。
对于大规模的图数据，GNN 通常使用采样、聚合等方法来减少计算量和存储量。
GNN 通常会采用多层模型，并多次迭代地更新节点表示以达到更好的表现效果。

图神经网络的实用框架

图神经网络目前有多种可用的实用框架，以下是其中比较流行的几个实用框架：

PyTorch Geometric（https://pytorch-geometric.readthedocs.io/en/latest/）
是使用 PyTorch 建立的一个处理图结构数据的计算库，它支持大量的传统图算法和 Graph Neural Network （GNN）算法。该框架适用于处理大规模、高维度的图结构数据。
Deep Graph Library（https://www.dgl.ai/）
是一个用于处理图结构数据的深度学习库，支持多种深度学习模型，如图卷积网络、图注意力网络等。该框架适用于处理大规模、分布式图结构数据。
GraphConv（https://github.com/mdeff/cnn_graph）
是一个使用 TensorFlow 实现的 GNN 框架，尤其适用于处理空间二维数据的图结构信息。该框架的核心是使用图卷积网络对图的节点进行卷积操作，以提取特征信息。
Deep Graph Nets（https://github.com/dsgiitr/dgmc）
是一个使用 TensorFlow 实现的动态图神经网络（Dynamic Graph Neural Networks, DGN）框架，可以对不同的图动态编辑和更新，从而适应更加复杂的场景。

以上实用框架都提供了完备的图神经网络算法模型和相应的实现方式，使用时可以根据具体需求进行选择。

GCN

对于一个输入图，他有N个节点，每个节点的特征组成一个特征矩阵X，节点与节点之间的关系组成一个邻接矩阵A，X和A即为模型的输入。

GCN是一个神经网络层，它具有以下逐层传播规则：
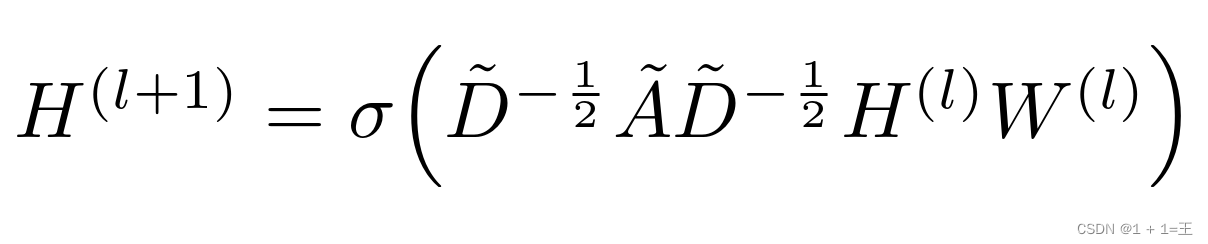
在这里插入图片描述

其中，

˜A = A + I，A为输入图的领接矩阵，I为单位矩阵。
˜D为˜A的度矩阵，˜D_ii = ∑_j ˜A_ij
H是每一层的特征，对于输入层H = X
σ是非线性激活函数
W为特定层的可训练权重矩阵

经过多层GCN逐层传播，输入图的特征矩阵由X变为Z，但邻接矩阵A始终保持共享，如下图：
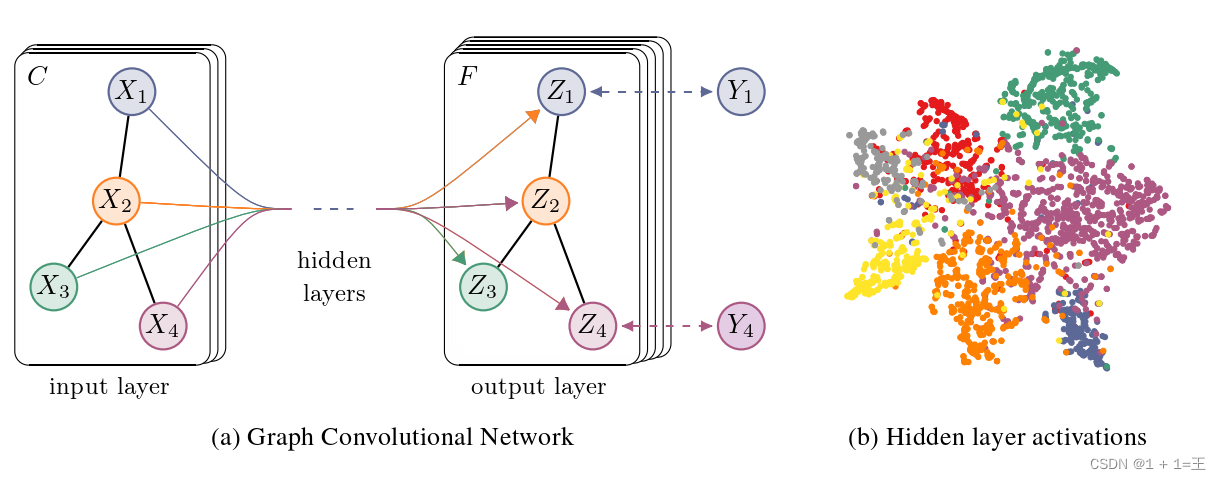在这里插入图片描述可以使用pyg（torch_geometric）搭建GCN网络：

import torch
import torch.nn as nn
from torch_geometric.nn import GCNConv
import torch.nn.functional as F


class GCN(torch.nn.Module):
    def __init__(self, in_channels, hidden_channels, out_channels):
        super().__init__()

        self.conv1 = GCNConv(in_channels, hidden_channels)
        self.conv2 = GCNConv(hidden_channels, out_channels)

    def forward(self, x, edge_index):
        x = self.conv1(x, edge_index)
        x = x.relu()
        x = F.dropout(x, p=0.5, training=self.training)
        x = self.conv2(x, edge_index)
        return x