这一节我们主要是将之前的知识穿起来,形成一个整体。如果之前的没看过可以回翻一下专栏。但是在整体回归之前,我们还需要学习一个小知识点——随机初始化
随机初始化
在神经网络中,我们大致的训练流程就是:通过前向传播得出当前 θ \theta θ下的假设结果,使用代价函数对比得到的假设结果和实际结果y,然后使用反向传播和梯度下降修正 θ \theta θ,使得 J ( θ ) J(\theta) J(θ)最小。但是在第一次进行前向传播的时候,就需要对 θ \theta θ赋予一定的初值,而简单地将所有的 θ \theta θ设置为0是不可行的。如果是这样的话,会导致所有的隐藏层都计算出同样的的结果,因此在开始之前,我们需要对一开始的 θ \theta θ进行随机初始化
很多编程语言都提供了取随机数的内置函数,我们可以规定 θ ∈ [ − ϵ , ϵ ] \theta \in [-\epsilon ,\epsilon ] θ∈[−ϵ,ϵ],比如可以这样进行随机初始化: θ = r a n d ( 0 , 1 ) ∗ ( 2 ∗ ϵ ) − ϵ \theta=rand(0,1)*(2*\epsilon)-\epsilon θ=rand(0,1)∗(2∗ϵ)−ϵ,其中rand(0,1)表示在0到1中随机取一个实数
神经网络流程整合
神经网络的流程如下:
1.选择一种架构
首先我们呢根据需要选择一种模型,决定有多少个隐藏层,每个隐藏层有多少个单元。输入层单元和样例特征有关,而输出层则和你需要分类的类别数量有关。有关于如何选择隐藏层的数目后面会介绍
2.随机初始化网络的参数
3.执行前向传播算法
通过前向传播算法,对于任意一个实例
x
(
i
)
x^{(i)}
x(i),得出其假设函数
h
θ
(
x
(
i
)
)
h_\theta(x^{(i)})
hθ(x(i)),这部分在https://blog.csdn.net/weixin_45434953/article/details/131048661的2.2
3.使用计算出的结果计算代价函数
使用各个实例的y和计算出来的
h
θ
(
x
(
i
)
)
h_\theta(x^{(i)})
hθ(x(i))根据公式计算出代价函数
J
(
Θ
)
J(\Theta)
J(Θ),这部分和下面的4.都在https://blog.csdn.net/weixin_45434953/article/details/131210254
4.使用反向传播计算出 ∂ ∂ Θ i j ( l ) J ( Θ ) \frac{\partial}{\partial\Theta_{ij}^{(l)}}J(\Theta) ∂Θij(l)∂J(Θ)
5.使用梯度检测检查梯度下降是否正常
当反向传播和数值估计所得到的导数值近似的时候,才能保证梯度下降正常工作,这一部分在https://blog.csdn.net/weixin_45434953/article/details/131171613,检查结束后记得关闭梯度检测
6.使用最优化算法得出最优的
θ
\theta
θ
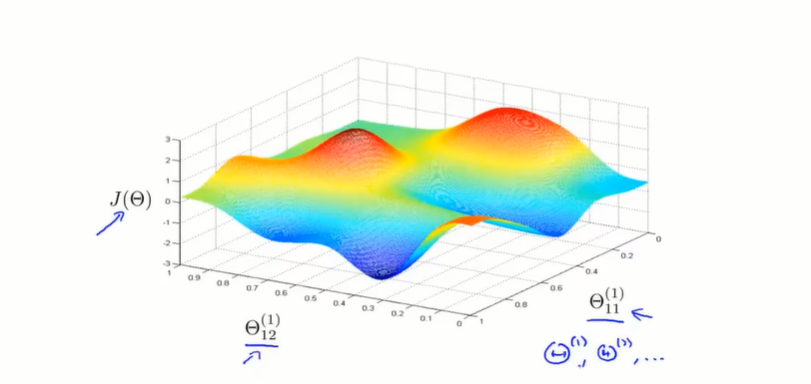
使用最优化算法,比如梯队下降,并且结合梯度下降来最小化假设函数
J
(
θ
)
J(\theta)
J(θ),得到最小化假设函数后的
θ
\theta
θ则是局部最优的参数取值,之所以是局部最优是因为假设函数图像也许拥有多个局部最优值