​

什么是树状数组？

树状数组是类似线段树的一个数据结构，支持单点修改、查询，区间修改、查询等操作，当你用查分TLE时，你就可以用树状数组解决。

树状数组和线段树的区别

树状数组代码简单适合用于简单一点的题目，而线段树结构复杂，代码较长，用于难题更为方便。

树状数组的结构

树状数组形似二叉树，却不是树形结构，其本质在于它每一个节点的的父节点，不是根据当前节点编号/2或除以2-1来确定的（注：这是二叉树的性质），而是通过计算lowbit值来确定（下文会讲到含义及计算方法）。

元素个数为8的序列的树状数组结构呈现是这样的：

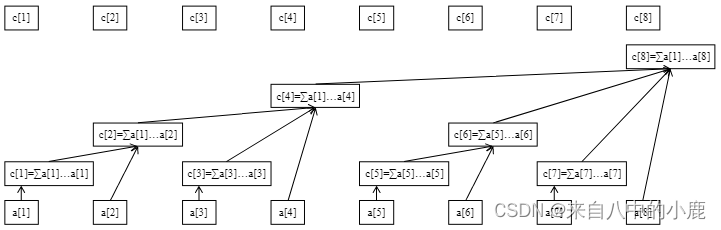
什么是lowbit

lowbit是树状数组中计算一个节点指向另外哪一个节点的函数。就如图1号节点指向的是2号节点是因为1的lowbit值为2，而6号节点指向8号节点是因为6的lowbit值为8.

lowbit如何计算

很简单，只需要计算一下x&-x就行了。

举个例子：6

6的二进制编码为1110，而它的反码（即-6的二进制）为1001，进行&运算得：1000，即8的二进制编码。

代码实现：

int lowbit(int x) {
  return x & -x;
}

​

补充知识——&，|，^运算

&

当遇到两个二进制数数（若不是二进制数就转换为二进制数）分别比较每一位，若都为1，则结果为1，否则结果为0.

|

若两个数中，有一个数为1，结果为1，否则为0。

^

即|的逆运算（取反），也就是，若两个数中，若有一个数为，结果为0，否则为1

注意：

以上运算最好是二进制数或bool类型，若不是，请先转换。

树状数组的基本操作

单点修改

单点修改非常简单，只要把包含了这个节点的所有节点都修改就行了。

while循环版代码

void add(int x, int k) {
  while (x <= n) {
    c[x] = c[x] + k;
    x = x + lowbit(x);
  }
}

for循环版代码

void add(int x, int k) {
  for(int i = x; i <= n; i+=lowbit(i){
  	c[i] = c[i] + k;
  }
}

因为我们已知每个点的父节点编号都是它的lowbit值，所以我们每次只用加lowbit，就可以轻松获取父节点编码。

单点查询

区间修改

区间查询

区间查询可以近似看做算前缀和。

int getsum(int x) {  // a[1]..a[x]的和
  int ans = 0;
  while (x > 0) {
    ans = ans + c[x];
    x = x - lowbit(x);
  }
  return ans;
}

树状数组的性质