文章目录
- 曲面
- 曲线
- 平面
- 点法式方程
- 不共线的3点确定一个平面
- 方程同解
- 平面方程的一般式
- 特别情形
- 与坐标轴平行的平面
- 与坐标轴垂直@与坐标面平行的平面
- A=B=C=0
- 例
- 截距式
- 两平面的夹角👺
- 两平面的位置关系
- 垂直关系
- 平行关系
- 例
- 点到平面的距离
- 小结
- 例
曲面
- 空间解析几何中"曲面S"的三元方程
G
:
F
(
x
,
y
,
z
)
=
0
G:F(x,y,z)=0
G:F(x,y,z)=0的关系(含义)
- S上的任意一点满足方程G
- 不在S上的点,不满足方程G
曲线
-
可以将空间曲线看作是曲面的交线
-
设2个曲面及其方程 S 1 : F ( x , y , z ) = 0 S_1:F(x,y,z)=0 S1:F(x,y,z)=0和 S 2 : G ( x , y , z ) = 0 S_2:G(x,y,z)=0 S2:G(x,y,z)=0
-
它们的交线 C C C的方程:
- F ( x , y , z ) = 0 G ( x , y , z ) = 0 F(x,y,z)=0\\ G(x,y,z)=0 F(x,y,z)=0G(x,y,z)=0
-
平面
点法式方程
-
一个平面 Π \Pi Π可以有一个位于 Π \Pi Π上的点 M 0 M_0 M0及 Π \Pi Π的法向量 n = ( A , B , C ) \boldsymbol{n}=(A,B,C) n=(A,B,C)所确定
-
平面上的任意一条直线总是和平面的法向量垂直,利用这个关系,可以构造平面的方程
-
平面上的任意一点 M ( x , y , z ) M(x,y,z) M(x,y,z), M 0 M → = ( x − x 0 , y − y 0 , z − z 0 ) \overrightarrow{M_0M}=(x-x_0,y-y_0,z-z_0) M0M=(x−x0,y−y0,z−z0)
-
则 M 0 M → ⋅ n = 0 \overrightarrow{M_0M}\cdot{\boldsymbol{n}}=0 M0M⋅n=0即
- A ( x − x 0 ) + B ( y − y 0 ) + C ( z − z 0 ) = 0 A(x-x_0)+B(y-y_0)+C(z-z_0)=0 A(x−x0)+B(y−y0)+C(z−z0)=0
-
不共线的3点确定一个平面
-
三个点可以唯一确定三维空间中的一个平面
-
设给定三个点 M 1 , M 2 , M 3 M_1,M_2,M_3 M1,M2,M3构成的向量 M 1 M 2 → , M 1 M 3 → \overrightarrow{M_1M_2},\overrightarrow{M_1M_3} M1M2,M1M3不共线,则三点确定的平面 Π \Pi Π的法向量可以由叉积确定:
-
n = M 1 M 2 → × M 1 M 3 → \boldsymbol{n}=\overrightarrow{M_1M_2}\times\overrightarrow{M_1M_3} n=M1M2×M1M3
-
再从 M 1 ∼ 3 M_{1\sim{3}} M1∼3中任选一点和 n \boldsymbol{n} n可以得到平面的点法式方程
-
方程同解
- 对于方程 F = G F=G F=G和 A = B A=B A=B,则 F + A = G + B F+A=G+B F+A=G+B或 F + B = G + A F+B=G+A F+B=G+A
平面方程的一般式
- 设方程
F
(
x
,
y
,
z
)
=
0
F(x,y,z)=0
F(x,y,z)=0,点
M
0
=
(
x
0
,
y
0
,
z
0
)
M_0=(x_0,y_0,z_0)
M0=(x0,y0,z0)满足
F
(
x
0
,
y
0
,
z
0
)
=
0
F(x_0,y_0,z_0)=0
F(x0,y0,z0)=0
- A x + B y + C z + D = 0 Ax+By+Cz+D=0 Ax+By+Cz+D=0
- A x 0 + B y 0 + C z 0 + D = 0 Ax_0+By_0+Cz_0+D=0 Ax0+By0+Cz0+D=0
- A ( x − x 0 ) + B ( y − y 0 ) + C ( z − z 0 ) = 0 A(x-x_0)+B(y-y_0)+C(z-z_0)=0 A(x−x0)+B(y−y0)+C(z−z0)=0(由1,2两式相减)
- 根据方程的性质,方程1和3是同解的,而方程3的形式是平面的点法式方程
- 方程3是过点 M 0 ( x 0 , y 0 , z 0 ) M_0(x_0,y_0,z_0) M0(x0,y0,z0)的且以 n = ( A , B , C ) \boldsymbol{n}=(A,B,C) n=(A,B,C)为法向量的平面 Π \Pi Π的点法式方程
- 可见,任意一个形如方程1的一元三次方程可以作为某个平面的方程,方程1称为平面的一般方程
特别情形
- 立体几何中
- 平面 Π \Pi Π与其外的直线 l \boldsymbol{l} l平行的充要条件是 Π \Pi Π中存在一条直线 t t t满足 t / / l t//l t//l,即 Π \Pi Π的法向量 n ⊥ l \boldsymbol{n}\perp{l} n⊥l
- 平面 Π \Pi Π与其外的直线 l \boldsymbol{l} l垂直的充要条件是 n / / l \boldsymbol{n}//\boldsymbol{l} n//l
- D = 0 D=0 D=0时,方程1(记为 E 1 E_1 E1)表示一个通过原点的平面(此时 ( 0 , 0 , 0 ) (0,0,0) (0,0,0)满足方程( E 1 ( D = 0 ) E_1(D=0) E1(D=0)))
与坐标轴平行的平面
- 这里的平行包含了坐标轴位于平面上的情形
-
A
=
0
A=0
A=0时,
E
1
E_1
E1退化为
E
1
(
A
=
0
)
:
B
y
+
C
z
+
D
=
0
E_1(A=0):By+Cz+D=0
E1(A=0):By+Cz+D=0此时方程仅剩下2个变量;此时平面上的任意点沿着
x
x
x轴平移任意距离依然位于平面上,可见
E
1
(
A
=
0
)
E_1(A=0)
E1(A=0)是一个平行于
x
x
x轴的平面
- 以平面法向量的角度来看, E 1 ( A = 0 ) E_1(A=0) E1(A=0)的法向量是 ( 0 , B , C ) (0,B,C) (0,B,C)其特点是位于坐标面 y O z yOz yOz上(和 x x x轴垂直)
- B = 0 B=0 B=0时, E 1 ( B = 0 ) E_1(B=0) E1(B=0)是一个平行于 y y y轴的平面
- C = 0 C=0 C=0时, E 1 ( C = 0 ) E_1(C=0) E1(C=0)是一个平行于 z z z轴的平面
与坐标轴垂直@与坐标面平行的平面
- 若 A , B , C A,B,C A,B,C中的2个为0,则平面平行于坐标面
- 例如A=B=0,平面的法向量为
(
0
,
0
,
C
)
(0,0,C)
(0,0,C)平行于z轴,此时平面垂直于z轴(平行于坐标面)
- 假设平面的法向量平行于z轴(设为(0,0,1),且平面过(1,1,1),方程为
z
+
D
=
0
z+D=0
z+D=0,记为
S
1
:
z
=
−
D
S_1:z=-D
S1:z=−D
- 此时,所有位于满足 z = − D z=-D z=−D的点都满足方程 S 1 S_1 S1
- 可以判断,满足 S 1 S_1 S1的所有点构成一个平行于 x O y xOy xOy坐标面的平面(或说垂直于 z z z轴的平面)
- 此时方程形如
C
z
+
D
=
0
Cz+D=0
Cz+D=0
- 假设点
(
1
,
0
,
0
)
(1,0,0)
(1,0,0)位于该平面上,则
D
=
0
D=0
D=0,因此
C
z
=
0
Cz=0
Cz=0
- 由于z=0,所以 C ∈ R C\in\mathbb{R} C∈R
- C z = 0 Cz=0 Cz=0,即 z = 0 C = 0 z=\frac{0}{C}=0 z=C0=0, z = 0 z=0 z=0表示 x O y xOy xOy坐标面
- 假设点(1,1,1)位于该平面,
C
+
D
=
0
C+D=0
C+D=0,
D
=
−
C
D=-C
D=−C,
- 平面 x O y xOy xOy的方程可以表示为 C z − C = 0 Cz-C=0 Cz−C=0,方程两边同时除以 C C C,得到 z − 1 = 0 z-1=0 z−1=0,即 z = 1 z=1 z=1
- 假设点
(
1
,
0
,
0
)
(1,0,0)
(1,0,0)位于该平面上,则
D
=
0
D=0
D=0,因此
C
z
=
0
Cz=0
Cz=0
- 假设平面的法向量平行于z轴(设为(0,0,1),且平面过(1,1,1),方程为
z
+
D
=
0
z+D=0
z+D=0,记为
S
1
:
z
=
−
D
S_1:z=-D
S1:z=−D
A=B=C=0
- 这种情况下,法向量变为 ( 0 , 0 , 0 ) (0,0,0) (0,0,0)这是个零向量,其方向是任意的,此时方程变为 0 = 0 0=0 0=0,不在表示平面
例
- 求过点
M
(
4
,
−
3
,
−
1
)
M(4,-3,-1)
M(4,−3,−1)和
x
x
x轴的平面
Π
\Pi
Π的方程
- 设平面方程一般式为 A x + B y + C z + D = 0 Ax+By+Cz+D=0 Ax+By+Cz+D=0
- 由于 Π \Pi Π过 x x x轴,则 ( 0 , 0 , 0 ) , ( x 0 , 0 , 0 ) , x 0 ∈ R (0,0,0),(x_0,0,0),x_0\in{\mathbb{R}} (0,0,0),(x0,0,0),x0∈R位于 Π \Pi Π,所以 D = 0 D=0 D=0且 A x 0 + 0 + 0 + 0 = 0 Ax_0+0+0+0=0 Ax0+0+0+0=0,即 A = 0 A=0 A=0
- 此时方程为 B y + C z = 0 By+Cz=0 By+Cz=0
- 带入 M M M,则 − 3 B − C = 0 -3B-C=0 −3B−C=0,即 C = − 3 B C=-3B C=−3B
- 从而
B
y
+
C
z
=
B
y
−
3
B
z
=
0
By+Cz=By-3Bz=0
By+Cz=By−3Bz=0,
- 若 B ≠ 0 B\neq{0} B=0对 B y − 3 B z = 0 By-3Bz=0 By−3Bz=0两边同除以 B B B,得到 y − 3 z = 0 y-3z=0 y−3z=0
- 若 B = 0 B=0 B=0,则方程为 0 = 0 0=0 0=0不是一个平面
- Note:
- 由
x
x
x轴位于平面
Π
\Pi
Π上可知,
Π
\Pi
Π的法向量
n
\boldsymbol{n}
n在
x
x
x轴上的投影为0
- Prj x n = ∣ n ∣ cos < x , n > = ∣ n ∣ cos π 2 = 0 \text{Prj}_{\boldsymbol{x}}\boldsymbol{n}=|\boldsymbol{n}|\cos<\boldsymbol{x,n}>=|\boldsymbol{n}|\cos\frac{\pi}{2}=0 Prjxn=∣n∣cos<x,n>=∣n∣cos2π=0(其中 x \boldsymbol{x} x表示 x x x轴)
- 从而 A A A
- 由
x
x
x轴位于平面
Π
\Pi
Π上可知,
Π
\Pi
Π的法向量
n
\boldsymbol{n}
n在
x
x
x轴上的投影为0
截距式
-
设平面 Π \Pi Π与 x , y , z x,y,z x,y,z轴的交点依次为$P(a,0,0),Q(0,b,0),R(0,0,c) 3 点 , 求 3点,求 3点,求\Pi$的方程
-
设平面的方程为 A x + B y + C z + D = 0 Ax+By+Cz+D=0 Ax+By+Cz+D=0
-
将 P , Q , R P,Q,R P,Q,R分别带入方程:
- a A + D = 0 b B + D = 0 c C + D = 0 aA+D=0\\ bB+D=0\\ cC+D=0 aA+D=0bB+D=0cC+D=0
-
解得
- A = − 1 a D B = − D b C = − D c A=-\frac{1}{a}D \\ B=-\frac{D}{b} \\ C=-\frac{D}{c} A=−a1DB=−bDC=−cD
-
从而 A x + B y + C z + D = 0 Ax+By+Cz+D=0 Ax+By+Cz+D=0即为 − D a x − D b y − D c z + D = 0 -\frac{D}{a}x-\frac{D}{b}y-\frac{D}{c}z+D=0 −aDx−bDy−cDz+D=0,两边同乘以 − 1 D , D ≠ 0 \frac{-1}{D},D\neq{0} D−1,D=0并移项,得到截距式
- x a + y b + z c = 1 \frac{x}{a}+\frac{y}{b}+\frac{z}{c}=1 ax+by+cz=1
-
两平面的夹角👺
-
这部分和高中数学内容向重合
-
两平面的夹角(通常记为 θ \theta θ, θ ∈ [ 0 , π 2 ] \theta\in[0,\frac{\pi}{2}] θ∈[0,2π]内的角)称为两平面的夹角
-
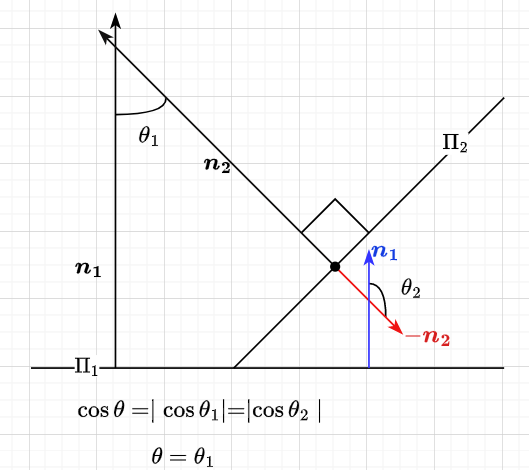
设平面 Π 1 , Π 2 \Pi_1,\Pi_2 Π1,Π2的法线向量依次为 n 1 = ( A 1 , B 1 , C 1 ) \boldsymbol{n_1}=(A_1,B_1,C_1) n1=(A1,B1,C1), n 2 = ( A 2 , B 2 , C 2 ) \boldsymbol{n_2}=(A_2,B_2,C_2) n2=(A2,B2,C2)
- θ 1 = < n 1 , n 2 > \theta_1=\boldsymbol{<n_1,n_2>} θ1=<n1,n2>, θ 2 = < − n 1 , n 2 > \theta_2=\boldsymbol{<-n_1,n_2>} θ2=<−n1,n2>, θ 1 + θ 2 = π \theta_1+\theta_2=\pi θ1+θ2=π
-
记平面 Π 1 , Π 2 \Pi_1,\Pi_2 Π1,Π2的夹角为 θ = min ( θ 1 , θ 2 ) \theta=\min(\theta_1,\theta_2) θ=min(θ1,θ2)
- 余弦函数满足 cos θ = − cos ( π − θ ) \cos\theta=-\cos(\pi-\theta) cosθ=−cos(π−θ)
-
因此 cos θ = ∣ cos ( θ 1 ) ∣ = ∣ θ ( θ 2 ) ∣ \cos\theta=|\cos(\theta_1)|=|\theta(\theta_2)| cosθ=∣cos(θ1)∣=∣θ(θ2)∣,也就是说,只要任意求出 cos θ 1 或 cos θ 2 \cos\theta_1或\cos\theta_2 cosθ1或cosθ2,然后对其取绝对值就是 θ \theta θ的余弦值
-
而 cos θ i , i = 1 , 2 \cos\theta_i,i=1,2 cosθi,i=1,2的计算公式为
-
cos θ = ∣ cos θ i ∣ = ∣ n 1 ⋅ n 2 ∣ n 1 ∣ ⋅ ∣ n 2 ∣ ∣ = ∣ A 1 A 2 + B 1 B 2 + C 1 C 2 ∣ A 1 2 + B 1 2 + C 1 2 A 2 2 + B 2 2 + C 2 2 \cos\theta=|\cos\theta_i| =\left| \frac{\boldsymbol{n_1\cdot n_2}}{\boldsymbol{|n_1|\cdot |n_2|}} \right| =\frac{|A_1A_2+B_1B_2+C_1C_2|} {\sqrt{A_1^2+B_1^2+C_1^2}\sqrt{A_2^2+B_2^2+C_2^2}} cosθ=∣cosθi∣= ∣n1∣⋅∣n2∣n1⋅n2 =A12+B12+C12A22+B22+C22∣A1A2+B1B2+C1C2∣
-
注意,该公式和两向量的夹角余弦公式的区别在于外围增加了一层"绝对值号"
-
-
两平面的位置关系
- 借助夹角来判断两个平面的平行和垂直关系
垂直关系
- 两个平面垂直,夹角 θ = π 2 \theta=\frac{\pi}{2} θ=2π,则 cos θ = 0 \cos\theta=0 cosθ=0,根据 cos θ \cos\theta cosθ的公式(上一节介绍的), A 1 A 2 + B 1 B 2 + C 1 C 2 = 0 A_1A_2+B_1B_2+C_1C_2=0 A1A2+B1B2+C1C2=0
平行关系
-
两个平面平行,夹角为 0 0 0或 π \pi π,则 cos θ = ± 1 \cos\theta=\pm{1} cosθ=±1,即 ∣ cos θ ∣ = 1 |\cos\theta|=1 ∣cosθ∣=1
-
∣ ∣ A 1 A 2 + B 1 B 2 + C 1 C 2 ∣ A 1 2 + B 1 2 + C 1 2 A 2 2 + B 2 2 + C 2 2 ∣ = 1 ( A 1 A 2 + B 1 B 2 + C 1 C 2 ) 2 = ( A 1 2 + B 1 2 + C 1 2 ) ( A 2 2 + B 2 2 + C 2 2 ) A 1 2 A 2 2 + B 1 2 B 2 2 + C 1 2 C 2 2 + 2 ( A 1 A 2 B 1 B 2 + A 1 A 2 C 1 C 2 + B 1 B 2 C 1 C 2 ) = A 1 2 A 2 2 + A 1 2 B 2 2 + A 1 2 C 2 2 + B 1 2 A 2 2 + B 1 2 B 2 2 + B 1 2 C 2 2 + C 1 2 A 2 2 + C 1 2 B 2 2 + C 1 2 C 2 2 2 ( A 1 A 2 B 1 B 2 + A 1 A 2 C 1 C 2 + B 1 B 2 C 1 C 2 ) = A 1 2 B 2 2 + A 1 2 C 2 2 + B 1 2 A 2 2 + B 1 2 C 2 2 + C 1 2 A 2 2 + C 1 2 B 2 2 A 1 2 B 2 2 + A 1 2 C 2 2 + B 1 2 A 2 2 + B 1 2 C 2 2 + C 1 2 A 2 2 + C 1 2 B 2 2 − 2 A 1 A 2 B 1 B 2 − 2 A 1 A 2 C 1 C 2 − 2 B 1 B 2 C 1 C 2 = 0 \left| \frac{|A_1A_2+B_1B_2+C_1C_2|} {\sqrt{A_1^2+B_1^2+C_1^2}\sqrt{A_2^2+B_2^2+C_2^2}} \right|=1 \\ (A_1A_2+B_1B_2+C_1C_2)^2=(A_1^2+B_1^2+C_1^2)(A_2^2+B_2^2+C_2^2) \\\\ A_1^2A_2^2+B_1^2B_2^2+C_1^2C_2^2+2(A_1A_2B_1B_2+A_1A_2C_1C_2+B_1B_2C_1C_2) \\=A_1^2A_2^2+A_1^2B_2^2+A_1^2C_2^2+B_1^2A_2^2+B_1^2B_2^2+B_1^2C_2^2 +C_1^2A_2^2+C_1^2B_2^2+C_1^2C_2^2 \\\\ 2(A_1A_2B_1B_2+A_1A_2C_1C_2+B_1B_2C_1C_2) \\=A_1^2B_2^2+A_1^2C_2^2+B_1^2A_2^2+B_1^2C_2^2 +C_1^2A_2^2+C_1^2B_2^2 \\\\ A_1^2B_2^2+A_1^2C_2^2+B_1^2A_2^2+B_1^2C_2^2 +C_1^2A_2^2+C_1^2B_2^2 \\-2A_1A_2B_1B_2-2A_1A_2C_1C_2-2B_1B_2C_1C_2=0 A12+B12+C12A22+B22+C22∣A1A2+B1B2+C1C2∣ =1(A1A2+B1B2+C1C2)2=(A12+B12+C12)(A22+B22+C22)A12A22+B12B22+C12C22+2(A1A2B1B2+A1A2C1C2+B1B2C1C2)=A12A22+A12B22+A12C22+B12A22+B12B22+B12C22+C12A22+C12B22+C12C222(A1A2B1B2+A1A2C1C2+B1B2C1C2)=A12B22+A12C22+B12A22+B12C22+C12A22+C12B22A12B22+A12C22+B12A22+B12C22+C12A22+C12B22−2A1A2B1B2−2A1A2C1C2−2B1B2C1C2=0
-
可得 ( A 1 B 2 − A 2 B 1 ) 2 + ( A 1 C 2 − A 2 C 1 ) 2 + ( B 1 C 2 − B 2 C 1 ) 2 = 0 (A_1B_2-A_2B_1)^2+(A_1C_2-A_2C_1)^2+(B_1C_2-B_2C_1)^2=0 (A1B2−A2B1)2+(A1C2−A2C1)2+(B1C2−B2C1)2=0
-
根据平方和为0的性质: ∑ f i 2 = 0 ⇔ f i = 0 \sum{f_i^2}=0\Leftrightarrow{f_i=0} ∑fi2=0⇔fi=0
- A 1 B 2 − A 2 B 1 = 0 A_1B_2-A_2B_1=0 A1B2−A2B1=0,即 A 1 B 2 = A 2 B 1 A_1B_2=A_2B_1 A1B2=A2B1,
- A 1 C 2 − A 2 C 1 = 0 A_1C_2-A_2C_1=0 A1C2−A2C1=0,即 A 1 C 2 = A 2 C 1 A_1C_2=A_2C_1 A1C2=A2C1
- B 1 C 2 − B 2 C 1 = 0 B_1C_2-B_2C_1=0 B1C2−B2C1=0,即 B 1 C 2 = B 2 C 1 B_1C_2=B_2C_1 B1C2=B2C1
-
若 A , B , C ≠ 0 A,B,C\neq{0} A,B,C=0(或说 A B C ≠ 0 ABC\neq{0} ABC=0)
- 两边乘以 1 A 2 B 2 \frac{1}{A_2B_2} A2B21,式1形式变换为 A 1 A 2 = B 1 B 2 \frac{A_1}{A_2}=\frac{B_1}{B_2} A2A1=B2B1类似的,可以得到 A 1 A 2 = C 1 C 2 \frac{A_1}{A_2}=\frac{C_1}{C_2} A2A1=C2C1, B 1 B 2 = C 1 C 2 \frac{B_1}{B_2}=\frac{C_1}{C_2} B2B1=C2C1
-
因此 A 1 A 2 = B 1 B 2 = C 1 C 2 \frac{A_1}{A_2}=\frac{B_1}{B_2}=\frac{C_1}{C_2} A2A1=B2B1=C2C1
- 虽然使用这个形式有 A B C ≠ 0 ABC\neq{0} ABC=0的条件,但是如果已知 Π 1 , Π 2 \Pi_1,\Pi_2 Π1,Π2的法向量满足该式,则 Π 1 / / Π 2 \Pi_1//{\Pi_2} Π1//Π2
- 在同济高数教材中,分母为0的情况用注脚做出了说明,约定在遇到分母为0的时候不再将其解释为除法(除以0),而是将分子视为0处理
-
例
- 平面
Π
\Pi
Π通过
M
1
(
1
,
1
,
1
)
,
M
2
(
0
,
1
,
−
1
)
M_1(1,1,1),M_2(0,1,-1)
M1(1,1,1),M2(0,1,−1)两点,
Π
0
:
x
+
y
+
z
=
0
\Pi_0:x+y+z=0
Π0:x+y+z=0,有关系
Π
⊥
Π
0
\Pi\perp{\Pi_0}
Π⊥Π0,求
Π
\Pi
Π
- 利用待定系数法求解
- 思路1:
- 设 Π \Pi Π的方程为 A x + B y + C z + D = 0 Ax+By+Cz+D=0 Ax+By+Cz+D=0
- 法向量为 n = ( A , B , C ) \boldsymbol{n}=(A,B,C) n=(A,B,C)
- 由 M 1 , 2 M_{1,2} M1,2在 Π \Pi Π上可知: A + B + C + D = 0 A+B+C+D=0 A+B+C+D=0, B − C + D = 0 B-C+D=0 B−C+D=0,两式相减 A + 2 C = 0 A+2C=0 A+2C=0
- 可求解出 E 1 : A = − 2 C E_1:A=-2C E1:A=−2C
- 思路2:设
Π
\Pi
Π的法向量为
n
=
(
A
,
B
,
C
)
\boldsymbol{n}=(A,B,C)
n=(A,B,C)
- m = M 1 M 2 → = ( − 1 , 0 , − 2 ) ∈ Π \boldsymbol{m}=\overrightarrow{M_1M_2}=(-1,0,-2)\in{\Pi} m=M1M2=(−1,0,−2)∈Π,所以 n ⊥ m \boldsymbol{n}\perp{\boldsymbol{m}} n⊥m
- 从而 m ⋅ n = 0 \boldsymbol{m\cdot{n}}=0 m⋅n=0,即 − A + 0 − 2 C = 0 -A+0-2C=0 −A+0−2C=0
- 可以解出 E 1 : A = − 2 C E_1:A=-2C E1:A=−2C
- 思路1:
- Π 0 \Pi_0 Π0的法向量为 n 0 = ( 1 , 1 , 1 ) \boldsymbol{n_0}=(1,1,1) n0=(1,1,1),由 Π ⊥ Π 0 \Pi\perp{\Pi_0} Π⊥Π0关系和上节中的结论: n ⋅ n 0 = 0 \boldsymbol{n\cdot{n_0}}=0 n⋅n0=0,即 E 2 : A + B + C = 0 E_2:A+B+C=0 E2:A+B+C=0
- 将 E 1 E_1 E1带入 E 2 E_2 E2,得 B = C B=C B=C;此时 n = ( A , B , C ) = ( − 2 C , C , C ) \boldsymbol{n}=(A,B,C)=(-2C,C,C) n=(A,B,C)=(−2C,C,C)
- 取 M 1 M_1 M1为点法式的点,构造方程 A ( x − 1 ) + B ( y − 1 ) + C ( z − 1 ) = 0 A(x-1)+B(y-1)+C(z-1)=0 A(x−1)+B(y−1)+C(z−1)=0,即 − 2 C ( x − 1 ) + C ( y − 1 ) + C ( z − 1 ) = 0 -2C(x-1)+C(y-1)+C(z-1)=0 −2C(x−1)+C(y−1)+C(z−1)=0
- 对两边同时除以C( C ≠ 0 C\neq 0 C=0),则 − 2 ( x − 1 ) + y − 1 + z − 1 = 0 -2(x-1)+y-1+z-1=0 −2(x−1)+y−1+z−1=0即 − 2 x + y + z = 0 -2x+y+z=0 −2x+y+z=0,即 2 x − y − z = 0 2x-y-z=0 2x−y−z=0
- 利用待定系数法求解
点到平面的距离
-
-
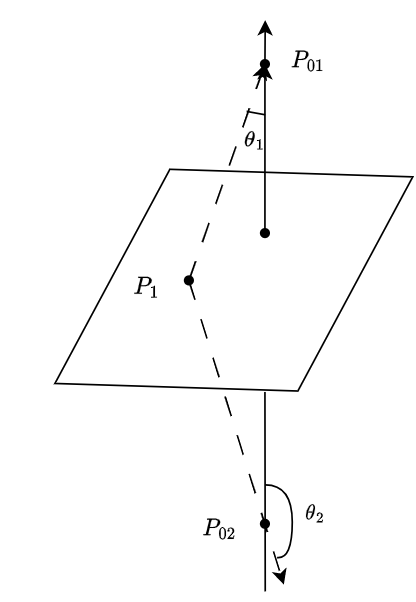
设 P 0 ( x 0 , y 0 , z 0 ) P_0(x_0,y_0,z_0) P0(x0,y0,z0)是平面 Π : A x + B y + C z + D = 0 \Pi:Ax+By+Cz+D=0 Π:Ax+By+Cz+D=0外一点,求 P 0 P_0 P0到 Π \Pi Π的距离 d d d
-
设平面的法向量为 n \boldsymbol{n} n,其朝向记为 d 1 \boldsymbol{d_1} d1, − n -\boldsymbol{n} −n也是 Π \Pi Π的法向量,其朝向记为 d 2 \boldsymbol{d_2} d2
-
我们只需要讨论其中的一种情况,另一种情况由于条件的对称性,同理,具有相同的结论
-
下面讨论点 P 0 P_0 P0位于 d 1 , d 2 \boldsymbol{d_1,d_2} d1,d2侧时的情形
-
将位于 d 1 \boldsymbol{d_1} d1侧时的 P 0 P_0 P0,记为 P 01 P_{01} P01,位于 d 2 \boldsymbol{d_2} d2侧时记为 P 02 P_{02} P02
-
分析可知,法向量 n \boldsymbol{n} n和 P 1 P 01 → \overrightarrow{P_{1}P_{01}} P1P01的夹角 θ 1 ∈ ( 0 , π 2 ) \theta_1\in(0,\frac{\pi}{2}) θ1∈(0,2π), n \boldsymbol{n} n和 P 1 P 02 → \overrightarrow{P_1P_{02}} P1P02的夹角为 θ 2 ∈ ( π 2 , π ) \theta_{2}\in(\frac{\pi}{2},\pi) θ2∈(2π,π)
-
距离分别记为 h 1 = ∣ P 1 P 01 → ∣ cos θ 1 h_1=|\overrightarrow{P_{1}P_{01}}|\cos{\theta_1} h1=∣P1P01∣cosθ1和 h 2 = ∣ P 1 P 02 → ∣ cos ( π − θ 2 ) = ∣ P 1 P 02 → ∣ ( − cos θ 2 ) h_2=|\overrightarrow{P_{1}P_{02}}|\cos{(\pi-\theta_2)}=|\overrightarrow{P_{1}P_{02}}|(-\cos{\theta_2)} h2=∣P1P02∣cos(π−θ2)=∣P1P02∣(−cosθ2)
-
其中 cos θ 2 < 0 \cos\theta_{2}<0 cosθ2<0,即 − cos θ 2 > 0 -\cos\theta_{2}>0 −cosθ2>0,从而 h 2 = ∣ P 1 P 02 → ∣ ∣ cos θ 2 ∣ h_2=|\overrightarrow{P_{1}P_{02}}||\cos{\theta_2|} h2=∣P1P02∣∣cosθ2∣
-
另一方面, cos θ 1 > 0 \cos\theta_1>0 cosθ1>0,即 ∣ cos θ 1 ∣ = cos θ 1 |\cos\theta_1|=\cos\theta_1 ∣cosθ1∣=cosθ1,从而 h 1 = ∣ P 1 P 01 → ∣ cos θ 1 = ∣ P 1 P 01 → ∣ ∣ cos θ 1 ∣ h_1=|\overrightarrow{P_{1}P_{01}}|\cos{\theta_1}=|\overrightarrow{P_{1}P_{01}}||\cos{\theta_1}| h1=∣P1P01∣cosθ1=∣P1P01∣∣cosθ1∣
-
从而 h 1 , h 2 h_1,h_2 h1,h2的计算公式形式一致,因此点 P 0 P_0 P0到 Π \Pi Π的距离公式为:
-
h = ∣ P 1 P 0 → ∣ ∣ cos θ ∣ h=|\overrightarrow{P_{1}P_{0}}||\cos{\theta}| h=∣P1P0∣∣cosθ∣
-
-
小结
-
P 1 P 0 → = ( x 0 − x 1 , y 0 − y 1 , z 0 − z 1 ) \overrightarrow{P_1P_0}=(x_0-x_1,y_0-y_1,z_0-z_1) P1P0=(x0−x1,y0−y1,z0−z1)
- h = ∣ P 1 P 0 → ∣ ∣ cos θ ∣ = ∣ P 1 P 0 → ∣ ∣ P 1 P 0 → ⋅ n ∣ ∣ P 1 P 0 → ∣ ∣ n ∣ = ∣ P 1 P 0 → ⋅ n ∣ ∣ n ∣ h=|\overrightarrow{P_1P_0}| |\cos\theta| =|\overrightarrow{P_1P_0}| \frac{|\overrightarrow{P_1P_0}\cdot{\boldsymbol{n}}|}{|\overrightarrow{P_1P_0}||\boldsymbol{n|}} \\ =\frac{|\overrightarrow{P_1P_0}\cdot{\boldsymbol{n}}|}{|\boldsymbol{n}|} h=∣P1P0∣∣cosθ∣=∣P1P0∣∣P1P0∣∣n∣∣P1P0⋅n∣=∣n∣∣P1P0⋅n∣
-
带入坐标式:
- h = ∣ ( x 0 − x 1 , y 0 − y 1 , z 0 − z 1 ) ⋅ ( A , B , C ) ∣ A 2 + B 2 + C 2 = ∣ A ( x 0 − x 1 ) + B ( y 0 − y 1 ) + C ( z 0 − z 1 ) ∣ A 2 + B 2 + C 2 = ∣ A x 0 − A x 1 + B y 0 − B y 1 + C z 0 − C z 1 ∣ A 2 + B 2 + C 2 = ∣ A x 0 + B y 0 + C z 0 − ( A x 1 + B y 1 + C z 1 ) ∣ A 2 + B 2 + C 2 h=\frac{|(x_0-x_1,y_0-y_1,z_0-z_1)\cdot(A,B,C)|} {\sqrt{A^2+B^2+C^2}} \\ =\frac{|A(x_0-x_1)+B(y_0-y_1)+C(z_0-z_1)|} {\sqrt{A^2+B^2+C^2}} \\ =\frac{|Ax_0-Ax_1+By_0-By_1+Cz_0-Cz_1|} {\sqrt{A^2+B^2+C^2}} \\ =\frac{|Ax_0+By_0+Cz_0-(Ax_1+By_1+Cz_1)|} {\sqrt{A^2+B^2+C^2}} h=A2+B2+C2∣(x0−x1,y0−y1,z0−z1)⋅(A,B,C)∣=A2+B2+C2∣A(x0−x1)+B(y0−y1)+C(z0−z1)∣=A2+B2+C2∣Ax0−Ax1+By0−By1+Cz0−Cz1∣=A2+B2+C2∣Ax0+By0+Cz0−(Ax1+By1+Cz1)∣
-
由于 P 1 ∈ Π P_1\in\Pi P1∈Π,所以 A x 1 + B y 1 + C z 1 + D = 0 Ax_1+By_1+Cz_1+D=0 Ax1+By1+Cz1+D=0,即 − ( A x 1 + B y 1 + C z ) = D -(Ax_1+By_1+C_z)=D −(Ax1+By1+Cz)=D
-
所以
- h = ∣ A x 0 + B y 0 + C z 0 + D ∣ A 2 + B 2 + C 2 h=\frac{|Ax_0+By_0+Cz_0+D|} {\sqrt{A^2+B^2+C^2}} h=A2+B2+C2∣Ax0+By0+Cz0+D∣
例
-
点 P ( 2 , 1 , 1 ) P(2,1,1) P(2,1,1)到 Π : x + y − z + 1 = 0 \Pi:x+y-z+1=0 Π:x+y−z+1=0的距离:
- h = ∣ 2 + 1 − 1 + 1 ∣ 1 + 1 + 1 = 3 h=\frac{|2+1-1+1|}{\sqrt{1+1+1}}=\sqrt{3} h=1+1+1∣2+1−1+1∣=3