概念

排序问题可以分为内部排序和外部排序。若整个排序过程不需要访问外存便能完成，则称此类排序问题为内部排序；反之，若参加排序的记录数量很大，整个序列的排序过程不可能在内存中完成，则称此类排序问题为外部排序。

在内部排序中，若对于两个相等的元素 $K i 和 K j （ i \neq = j ）$ ，在排序前的序列中 $R i$ 领先于 $R j$ （即 $i < j$ ），排序后的序列中 Ri 仍领先于 Rj，则称所用的排序方法是稳定的；反之，若可能使排序后的序列中 $R j$ 领先于 $R i$ ，则称所用的排序方法是非稳定的。

插入排序

插入排序的基本思想是将待排序的序列分成已排序和未排序的两部分，每次从未排序的部分取出第一个元素，插入到已排序部分合适的位置，直到未排序部分为空为止。具体操作如下：

在 $R [1.. i - 1]$ 中查找 $R [i]$ 的插入位置，使得 $R [1.. j] . k ey \leq R [i] . k ey < R [j + 1.. i - 1] . k ey$ ；
将 $R [j + 1.. i - 1]$ 中的所有记录均后移一个位置；
将 $R [i]$ 插入（复制）到 $R [j + 1]$ 的位置上。

这样就完成了一次插入操作，对于待排序的序列，重复执行以上操作直到全部排序完成。

直接插入排序

直接插入排序的基本思想是将待排序的序列分成已排序和未排序的两部分，每次从未排序的部分取出第一个元素，插入到已排序部分合适的位置，直到未排序部分为空为止。具体操作如下：

初始时，将 $R [1]$ 看作是有序区， $R [2.. n]$ 构成无序区；
依次将无序区的元素插入到有序区中，使得有序区始终有序。插入操作包括以下三步：
1）在 $R [1.. i - 1]$ 中查找 $R [i]$ 的插入位置，使得 $R [1.. j] . k ey \leq R [i] . k ey < R [j + 1.. i - 1] . k ey$ ；
2）将 $R [j + 1.. i - 1]$ 中的所有记录均后移一个位置；
3）将 $R [i]$ 插入（复制）到 $R [j + 1]$ 的位置上。
重复执行 2 直到无序区为空，排序完成。

void InsertionSort(SqList& L) {
    // 对顺序表 L 作直接插入排序
    for (int i = 2; i <= L.length; ++i) {
        if (L.r[i].key < L.r[i - 1].key) {
            // 将当前待排序的记录暂存到监视哨中，等待插入
            L.r[0] = L.r[i];
            int j;
            for (j = i - 1; L.r[0].key < L.r[j].key; --j) {
                // 将记录后移，寻找插入位置
                L.r[j + 1] = L.r[j];
            }
            L.r[j + 1] = L.r[0]; // 插入到正确位置
        }
    }
}

最好的情况：

序列顺序有序，比较的次数：n-1，移动的次数：0

最坏的情况：
在这里插入图片描述
时间复杂度大概 $O(n^2)$

其他插入排序

折半插入

void BiInsertionSort(SqList &L) {
    for (int i = 2; i <= L.length; ++i) {
        L.r[0] = L.r[i];      // 将 L.r[i] 暂存到 L.r[0]
        int low = 1, high = i - 1;
        while (low <= high) { 
            int mid = (low + high) / 2; // 折半
            if (L.r[0].key < L.r[mid].key)
                high = mid - 1;   // 插入点在低半区
            else
                low = mid + 1;    // 插入点在高半区
        }
        for (int j = i - 1; j >= high + 1; --j) {
            L.r[j + 1] = L.r[j];      // 记录后移
        }
        L.r[high + 1] = L.r[0];  // 插入
    } 
}

L.r[high + 1] = L.r[0]; // 插入是在 $hi g h + 1$ 的位置插入（此时，low>high）

希尔排序

希尔排序（又称缩小增量排序）

基本思想：对待排记录序列先作“宏观”调整，再作“微观”调整。所谓“宏观”调整，指的是“跳跃式”的插入排序。具体做法为：

1.将记录序列分成若干子序列，分别对每个子序列进行插入排序。

2.待整个序列中的纪录‘基本有序’时，再对全体记录进行一次直接插入排序。

例如：将 $n$ 个记录分成 $d$ 个子序列：

${ R[1]，R[1+d]，R[1+2d]，…，R[1+kd] }$

${ R[2]，R[2+d]，R[2+2d]，…，R[2+kd] }$

$\dots$

${ R[d]，R[2d]，R[3d]，…，R[kd]，R[(k+1)d] }$

其中， $d$ 称为增量，它的值在排序过程中从大到小逐渐缩小，直至最后一趟排序减为 1。

在这里插入图片描述

冒泡排序

void BubbleSort(Elem R[], int n) {
    int i = n;
    while (i > 1) { 
        int lastExchangeIndex = 1; 
        for (int j = 1; j < i; j++) {
            if (R[j+1].key < R[j].key) { 
                Swap(R[j], R[j+1]);
                lastExchangeIndex = j;
            } //if
        } //for
        i = lastExchangeIndex; // 本趟进行过交换的最后一个记录的位置          
    } // while
} // BubbleSort

起泡排序的结束条件为，最后一趟没有进行“交换记录”。
一般情况下，每经过一趟“起泡”，i减1，但并不是每趟都如此。具体来说，每一趟排序时，我们都记录下最后一次交换操作的位置，如果在一趟排序结束之后，最后一次交换操作的位置和上一趟排序结束时的位置相同，那么说明这次排序并没有进行任何交换操作，也就是说从该位置之后的元素已经有序。此时，我们便可以认为序列已经有序了，因此结束算法的执行。

在这里插入图片描述
时间复杂度大概 $O(n^2)$

快速排序

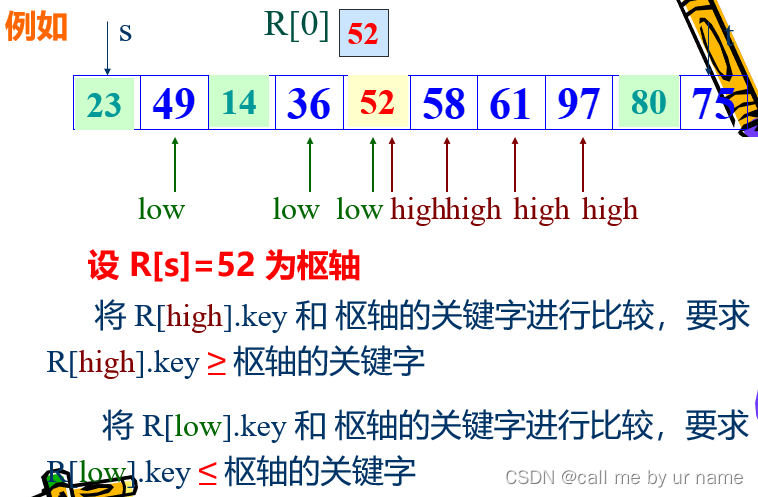
找一个记录，以它的关键字作为“枢轴”，凡其关键字小于枢轴的记录均移动至该记录之前，反之，凡关键字大于枢轴的记录均移动至该记录之后。

经过一趟排序之后，记录的无序序列 $R [s .. t]$ 将分割成两部分： $R [s .. i - 1]$ 和 $R [i + 1.. t]$ ，且 $R[j].key\leq R[i].key \leq R[p].key (s\leq j\leq i-1)~ 枢轴 ~(i+1\leq p\leq t)$ 其中 $i$ 表示枢轴记录的位置， $\leq i-1$ 的记录的关键字都小于等于枢轴的关键字， $\geq i+1$ 的记录的关键字都大于等于枢轴的关键字。注意，这里假设枢轴所在的位置不是 $s$ 或 $t$ ，否则就没有对应的一侧了。

在这里插入图片描述

int Partition (RedType& R[], int low, int high) {
    pivotkey = R[low].key;  // 用子表的第一个记录作枢轴记录
    while (low < high) {    // 从表的两端交替地向中间扫描
        while (low < high && R[high].key >= pivotkey)    
            --high;  
        R[low] ←→ R[high];   // 将比枢轴记录小的记录交换到低端
        while (low < high && R[low].key <= pivotkey) 
            ++low;   
        R[low] ←→ R[high];  // 将比枢轴记录大的记录交换到高端
    }
    return low;  // 返回枢轴所在位置
} // Partition

void QSort (RedType & R[], int low, int high) {
    // 对记录序列R[low..high]进行快速排序
    if (low < high) {  // 长度大于1
        pivotloc = Partition(R, low, high);
        // 对 R[s..t] 进行一次划分
        QSort(R, low, pivotloc - 1);
        // 对低子序列递归排序，pivotloc是枢轴位置
        QSort(R, pivotloc + 1, high); // 对高子序列递归排序
    }
} // QSort

时间复杂度： $O (n l o g n)$

选择排序

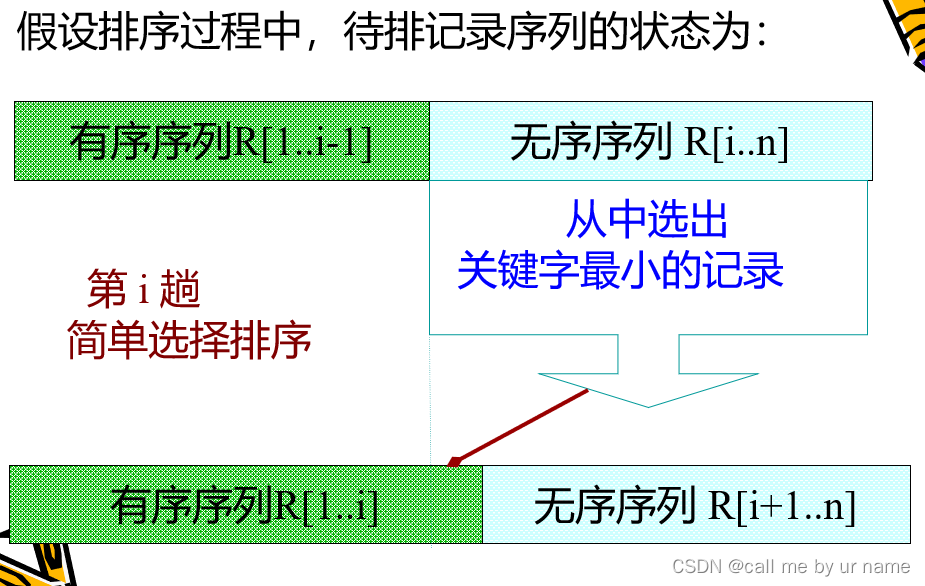
在这里插入图片描述
从未排序的序列选择一个最小的元素排到有序序列里

void SelectSort(Elem R[], int n) {
    // 对记录序列 R[1..n] 进行简单选择排序。
    for (int i = 1; i < n; ++i) {
        // 选择第 i 小的记录，并交换到位
        int j = SelectMinKey(R, i);
        // 在 R[i..n] 中选择关键字最小的记录
        if (i != j) {
            // 与第 i 个记录交换
            R[i] ↔ R[j];
        }
    }
} // SelectSort

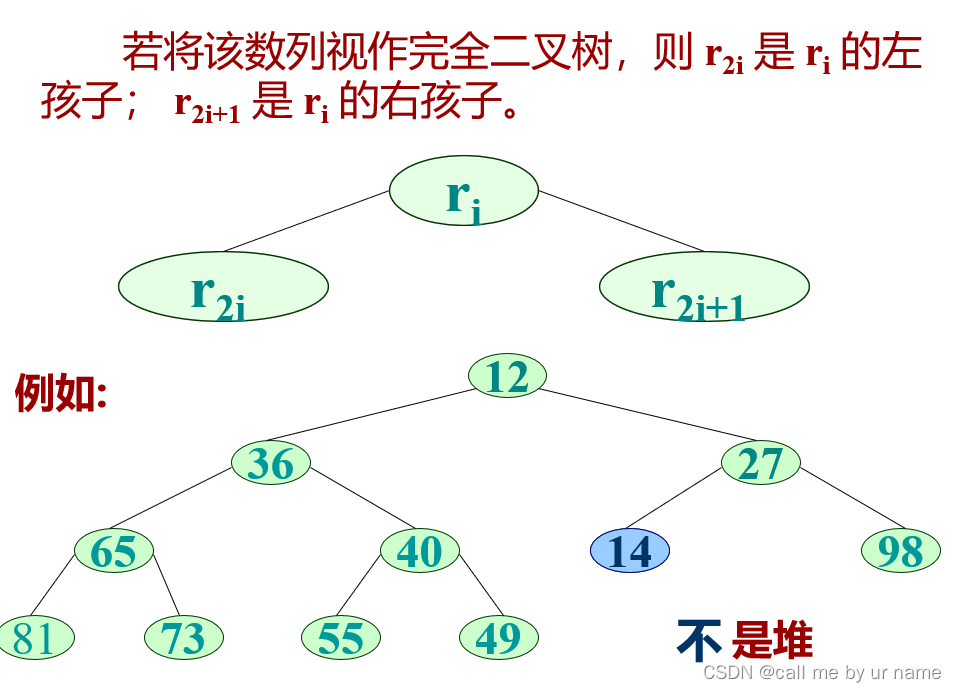
在这里插入图片描述

堆排序

在这里插入图片描述

光看定义还有点不太明白，但是根据树就应该很明晰了

建大顶堆

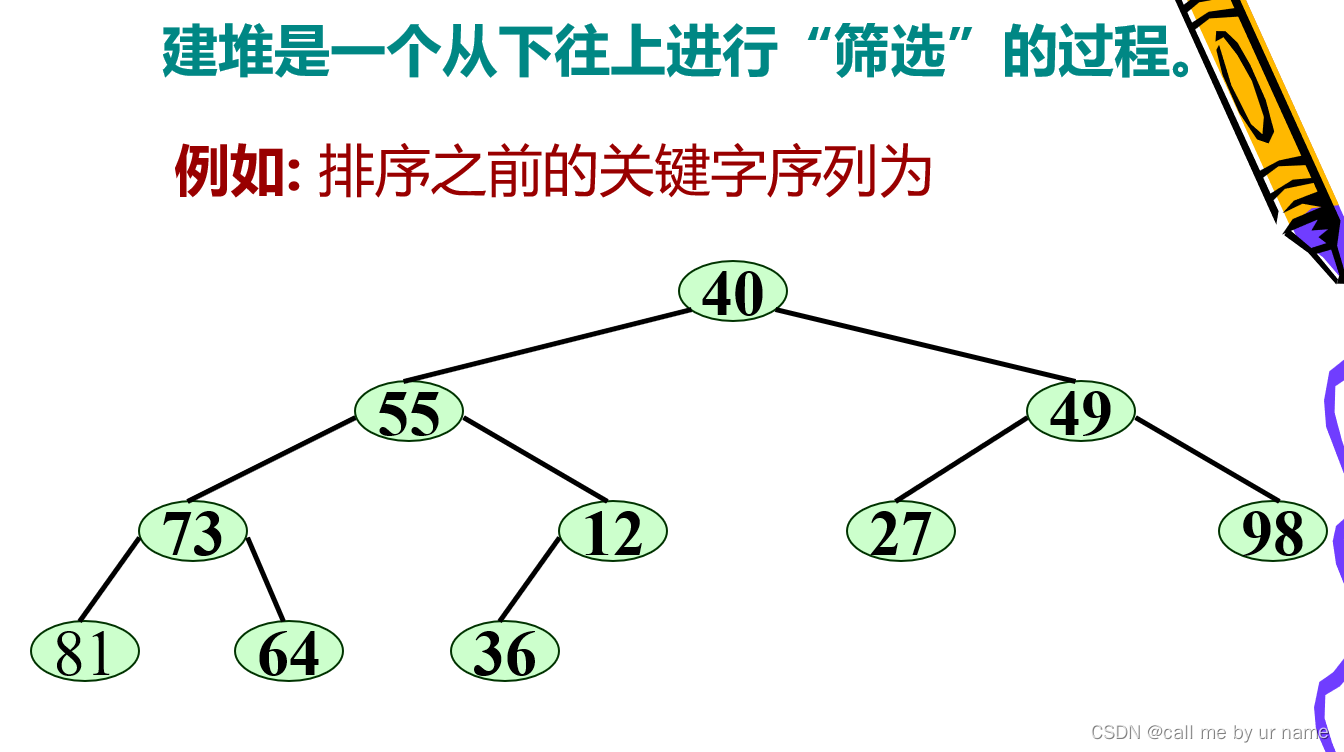
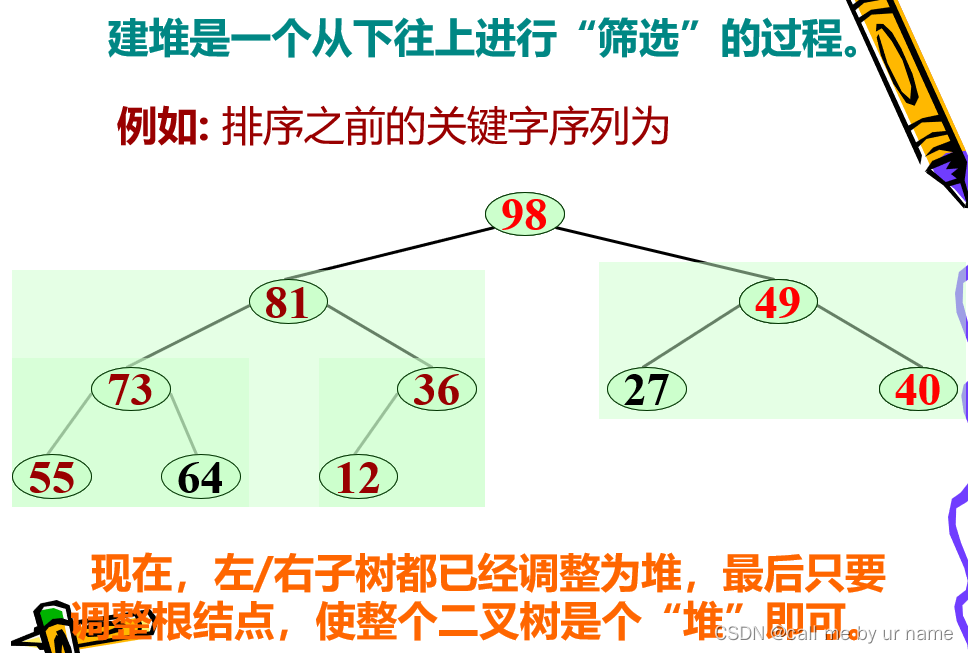
在这里插入图片描述

自下而上

习题

各个排序

在这里插入图片描述
后面2个考试不涉及

直接插入排序：503 087　512　061　908　170　897　275　653　426
第一趟结果：087　503 512　061　908　170　897　275　653　426
第二趟结果：087　503 512 061　908　170　897　275　653　426
第三趟结果：061　087 503 512 908　170　897　275　653　426
第四趟结果：061　087　503　512　908 170　897　275　653　426
第五趟结果：061　087　170　503　512　908 897　275　653　426
第六趟结果：061　087　170　503　512　897　908 275　653　426
第七趟结果：061　087　170　275　503　512　897　908 653　426
第八趟结果：061　087　170　275　503　512　653　897　908 426
第九趟结果：061　087　170　275　426　503　512　653　897　908
粗体为已经排好序的序列
希尔排序初始关键字： 503 087 512 061 908 170 897 275 653 426
第一趟结果：d[1]=5 170 087 275 061 426 503 897 512 653 908
第二趟结果：d[2]=3 061 087 275 170 426 503 897 512 653 908
第三趟结果：d[3]=1 061 087 170 275 426 503 512 653 897 908
主要注意一下希尔排序是以下标号的后x个作排序——在d[1]=5，a[0]=503是a[5]=170排序的
快速排序
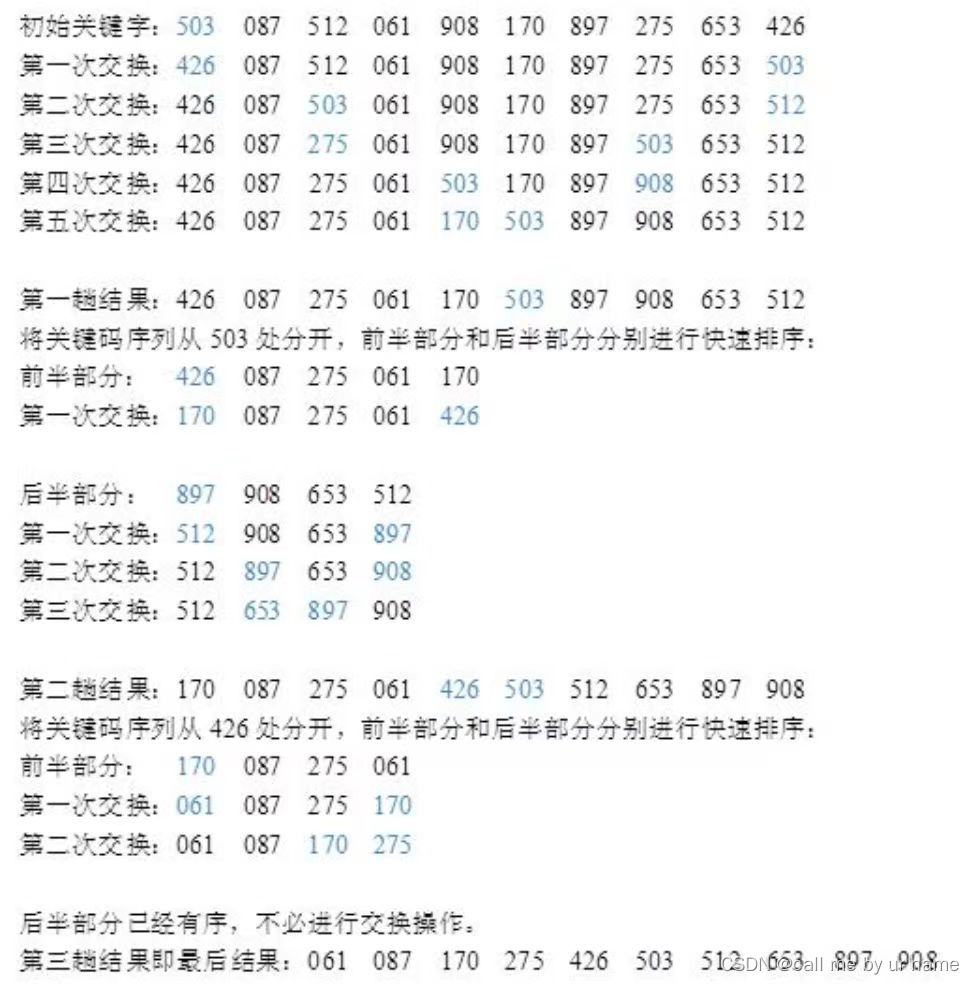
注意，快速排序不是把比Key小的数直接随便放到Key前面，是用low和high遍历出来的
堆排序

小顶堆

堆排序

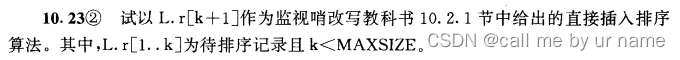
在这里插入图片描述

监视哨

在这里插入图片描述

void directInsertSort(int L[], int k) {
    int i, j;
    for (i = 2; i <= k; i++) {
        L[k+1] = L[i]; 
        j = i - 1;
        while (L[j] > L[0]) {
            L[j + 1] = L[j];
            j--;
        }
        L[j + 1] = L[0]; 
    }
}

设计算法

在这里插入图片描述

void process(int A[n]) {
    int low = 0;
    int high = n - 1;
    while (low < high) {
        while (low < high && A[low] < 0)
            low++;
        while (low < high && A[high] > 0)
            high++;
        if (low < high) {
            // 交换 A[low] 和 A[high]
            int temp = A[low];
            A[low] = A[high];
            A[high] = temp;
            low++;
            high--;
        }
    }
    return;
}

双指针法
时间复杂度 $O(n^2)$

荷兰国旗问题

在这里插入图片描述

typedef enum {RED, WHITE, BLUE} color; // 定义枚举类型表示三种颜色

void Flag_Arrange(color a[], int n) {
    int i = 0;
    int j = 0;
    int k = n - 1;

    while (j <= k) {
        switch (a[j]) {
            case RED:
                // a[i] 与 a[j] 交换
                // 增加 i 和 j 的值，同时继续处理下一个元素
                swap(a[i], a[j]);
                i++;
                j++;
                break;
            case WHITE:
                // 当遇到白色时，只需要将 j 向右移动一位
                j++;
                break;
            case BLUE:
                // a[j] 与 a[k] 交换
                // 不增加 j 的值，因为可能需要再次检查交换后的 a[j]
                // 减少 k 的值，将蓝色元素移至数组末尾
                swap(a[j], a[k]);
                k--;
                break;
        }
    }
}