实现异常情况检测算法，并应用它来检测网络上的故障服务器。

1 导包

import numpy as np
import matplotlib.pyplot as plt
from utils import *
from public_tests import *
%matplotlib inline

2 - 异常检测

2.1 问题陈述

在此练习中，您将实现一个异常检测算法来检测服务器计算机中的异常行为。

数据集包含两个特征 -

• 吞吐量（mb / s）和
• 每个服务器响应的延迟（ms）。

当您的服务器正在运行时，您收集了$m=307$个例子，记录它们的行为，因此有一个未标记数据集 { x ( 1 ) , … , x ( m ) } \{x^{(1)}, \ldots, x^{(m)}\} {x(1),…,x(m)}。

• 您怀疑其中绝大多数示例是服务器正常运行的“正常”（非异常）示例，但也可能有一些服务器在此数据集中表现异常。

您将使用高斯模型来检测数据集中的异常示例。

• 首先，您将从一个二维数据集开始，以便您可以可视化算法正在执行的操作。
• 在该数据集上，您将拟合高斯分布，然后找到概率非常低的值，因此可以被视为异常。
• 之后，您将把这个异常检测算法应用到具有许多维度的更大数据集上。

2.2 数据集

您将首先加载此任务的数据集。

• 下面显示的load_data()函数将数据加载到变量X_train，X_val和y_val中
  • 您将使用X_train拟合高斯分布
  • 您将使用X_val和y_val作为交叉验证集来选择阈值并确定异常与正常示例。

X_train, X_val,y_val = load_data()

X_train[:5]

array([[13.04681517, 14.74115241],
       [13.40852019, 13.7632696 ],
       [14.19591481, 15.85318113],
       [14.91470077, 16.17425987],
       [13.57669961, 14.04284944]])

X_val[:5]

array([[15.79025979, 14.9210243 ],
       [13.63961877, 15.32995521],
       [14.86589943, 16.47386514],
       [13.58467605, 13.98930611],
       [13.46404167, 15.63533011]])

y_val[:5]

array([0, 0, 0, 0, 0], dtype=uint8)

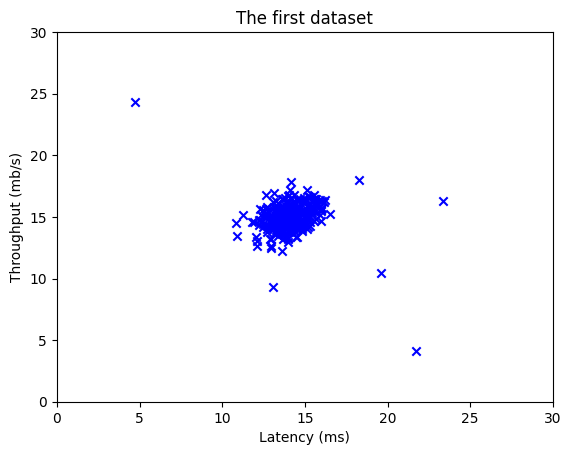
可视化您的数据

在开始任何任务之前，通过可视化数据通常很有用。

• 对于此数据集，由于它只有两个要绘制的属性（吞吐量和延迟），因此可以使用散点图来可视化数据（X_train）。

print(f"X_train的最大值{np.max(X_train)}，最小值{np.min(X_train)}")

X_train的最大值24.35040724802435，最小值4.126232224310076

plt.scatter(X_train[:, 0], X_train[:, 1], marker='x', c='b')
plt.title("The first dataset")
plt.ylabel('Throughput (mb/s)')
plt.xlabel('Latency (ms)')
plt.axis([0, 30, 0, 30])
plt.show()

2.3 高斯分布

要执行异常检测，首先需要拟合数据的分布模型。

• 给定训练集 { x ( 1 ) , . . . , x ( m ) } \{x^{(1)}, ..., x^{(m)}\} {x(1),...,x(m)}，你想要估计每个特征 $x_i$ 的高斯分布。

• 回忆一下，高斯分布由以下公式给出：

  $$p(x;\mu ,{\sigma }^2)=\frac{1}{\sqrt{2\pi {\sigma }^2}}{\exp }^{-\frac{(x-\mu {)}^2}{2{\sigma }^2}}$$

  其中 $\mu$ 是均值，${\sigma }^2$ 控制方差。

• 对于每个特征 $i=1\dots n$，你需要找到适合第 $i$ 维度 { x i ( 1 ) , . . . , x i ( m ) } \{x_i^{(1)}, ..., x_i^{(m)}\} {xi(1)​,...,xi(m)​}（每个样本的第 $i$ 维度）数据的参数 ${\mu }_i$ 和 ${\sigma }_i^2$。

2.2.1 估计高斯分布的参数

完成下面的 estimate_gaussian 函数来计算 X 中每个特征的均值 mu 和方差 var。

可以使用以下方程来估计第 $i$ 个特征的参数 (${\mu }_i$, ${\sigma }_i^2$)。为了估计平均值，你将使用：

$${\mu }_i=\frac{1}{m}\sum _{j=1}^m{x}_i^{(j)}$$

对于方差，你将使用：

$${\sigma }_i^2=\frac{1}{m}\sum _{j=1}^m(x_i^{(j)}-{\mu }_i{)}^2$$

def estimate_gaussian(x):
    m,n = x.shape
    # 平均值
    mu = 1 / m * np.sum(x,axis=0)
    # 方差
    var = 1/ m * np.sum((x-mu)**2,axis=0)
    return mu,var

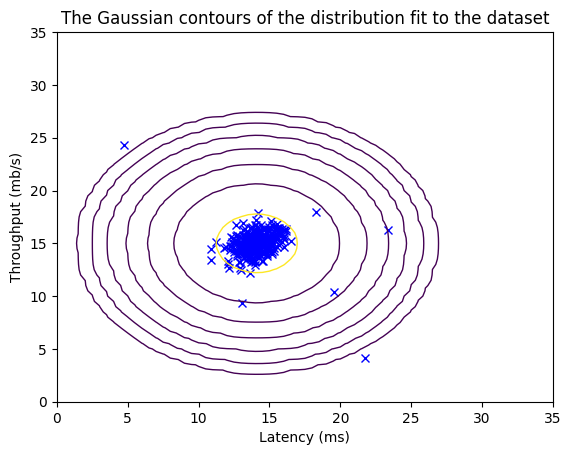
现在你已经完成了 estimate_gaussian 函数的编写，我们将可视化拟合的高斯分布的轮廓。

你应该会得到与下图类似的图形。

从你的图中可以看出，大多数样本都在最高概率的区域内，而异常样本则在概率较低的区域中。

mu, var = estimate_gaussian(X_train)

p = multivariate_gaussian(X_train,mu,var)
visualize_fit(X_train,mu,var)

2.2.2 选择阈值 $ϵ$

现在你已经估计了高斯分布参数，可以探究哪些样本在这个分布中有非常高的概率，哪些样本具有非常低的概率。

• 具有低概率的示例更可能是我们数据集中的异常点。
• 确定哪些示例是异常点的一种方法是根据交叉验证集选择阈值。

在本节中，你将完成 select_threshold 函数的编写，使用交叉验证集上的 $F_1$ 分数来选择阈值 $\epsilon$。

• 为此，我们将使用一个交叉验证集 $\{(x_{\mathrm{cv}}^{(1)},y_{\mathrm{cv}}^{(1)}),\dots ,(x_{\mathrm{cv}}^{(m_{\mathrm{cv}})},y_{\mathrm{cv}}^{(m_{\mathrm{cv}})})\}$，其中标签 $y=1$ 对应于异常示例，$y=0$ 对应于正常示例。
• 对于每个交叉验证示例，我们将计算 $p(x_{\mathrm{cv}}^{(i)})$。所有这些概率 $p(x_{\mathrm{cv}}^{(1)}),\dots ,p(x_{\mathrm{cv}}^{(m_{\mathrm{cv})}})$ 的向量将以 p_val 向量的形式传递给 select_threshold。
• 相应的标签 $y_{\mathrm{cv}}^{(1)},\dots ,y_{\mathrm{cv}}^{(m_{\mathrm{cv})}}$ 将以相同的方式传递给该函数，存储在 y_val 向量中。

请完成以下 select_threshold 函数，以找到基于验证集 (p_val) 和真实标签 (y_val) 的结果选择异常值所使用的最佳阈值。

• 在已提供的 select_threshold 代码中，已经有一个循环将尝试许多不同的 $\epsilon$ 值，并根据 $F_1$ 分数选择最佳 $\epsilon$。

• 你需要实现计算使用 epsilon 作为阈值的 F1 分数的代码，并将该值放入 F1 中。

  • 回想一下，如果一个样本 $x$ 具有较低的概率 $p(x)<\epsilon$，那么它被分类为异常点。

  • 然后，可以通过以下方式计算精确度和召回率：
    $$\begin{array}{rlr}prec& =& \frac{tp}{tp+fp}\\ rec& =& \frac{tp}{tp+fn},\end{array}$$ 其中

    • $tp$ 是真正例(true positives)的数量：即实际标签指示为异常值，我们的算法正确地将其分类为异常值。
    • $fp$ 是假正例(false positives)的数量：即实际标签指示为非异常值，但我们的算法错误地将其分类为异常值。
    • $fn$ 是假负例(false negatives)的数量：即实际标签指示为异常值，但我们的算法错误地将其分类为非异常值。

  • F1 分数使用精确度（$prec$）和召回率（$rec$）计算如下：
    $$F_1=\frac{2\cdot prec\cdot rec}{prec+rec}$$

实现提示：
为了计算 $tp$, $fp$ 和 $fn$，你可能可以使用矢量化实现，而不是循环遍历所有

def select_threshold(y_val, p_val):
    best_epsilon = 0
    best_F1 = 0
    F1 = 0

    step_size = (max(p_val) - min(p_val)) / 1000

    for epsilon in np.arange(min(p_val), max(p_val), step_size):


        predictions = (p_val < epsilon)
        tp = np.sum((predictions == 1) & (y_val == 1))
        fn = np.sum((predictions == 0) & (y_val == 1))
        fp = np.sum((predictions == 1) & (y_val == 0))
        # 精确率
        if (tp + fp) > 0:
            prec = tp / (tp + fp)
        else:
            prec = 0
        # 召回率
        rec = tp / (tp + fn)
        # 计算F1
        if (prec + rec) > 0:
            F1 = 2 * prec * rec / (prec + rec)
        else:
            F1 = 0
        if F1 > best_F1:
            best_F1 = F1
            best_epsilon = epsilon

    return best_epsilon, best_F1

p_val = multivariate_gaussian(X_val, mu, var)
epsilon, F1 = select_threshold(y_val, p_val)

print('Best epsilon found using cross-validation: %e' % epsilon)
print('Best F1 on Cross Validation Set: %f' % F1)

Best epsilon found using cross-validation: 8.990853e-05
Best F1 on Cross Validation Set: 0.875000

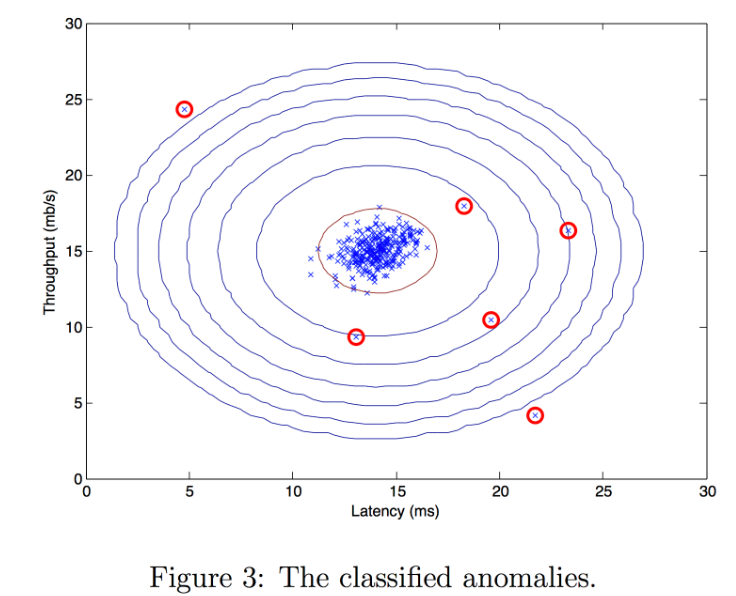
现在，我们将运行异常检测代码，并在图中圈出异常（下面的图 3）。

2.4 高维数据集

现在，我们将在一个更加现实且更难的数据集上运行您实现的异常检测算法。

在这个数据集中，每个样本由11个特征描述，捕捉了计算服务器的许多属性。

让我们从加载数据集开始。

• 下面显示的 load_data() 函数将数据加载到变量 X_train_high、X_val_high 和 y_val_high 中
  • _high 用于区分这些变量和前面部分中使用的变量
  • 我们将使用 X_train_high 来拟合高斯分布
  • 我们将使用 X_val_high 和 y_val_high 作为交叉验证集来选择阈值并确定异常和正常样本

X_train_high, X_val_high, y_val_high = load_data_multi()

print ('The shape of X_train_high is:', X_train_high.shape)
print ('The shape of X_val_high is:', X_val_high.shape)
print ('The shape of y_val_high is: ', y_val_high.shape)

The shape of X_train_high is: (1000, 11)
The shape of X_val_high is: (100, 11)
The shape of y_val_high is:  (100,)

异常检测

现在，让我们在这个新的数据集上运行异常检测算法。

下面的代码将使用您的代码来：

• 估计高斯参数 (${\mu }_i$ 和 ${\sigma }_i^2$)
• 对训练数据 X_train_high（从中估计了高斯参数）以及交叉验证集 X_val_high 计算概率。
• 最后，它将使用 select_threshold 来找到最佳阈值 $\epsilon$。

# 对更大的数据集应用相同的步骤

# 估计高斯分布的参数
mu_high, var_high = estimate_gaussian(X_train_high)

# 计算训练集数据的概率
p_high = multivariate_gaussian(X_train_high, mu_high, var_high)

# 计算交叉验证集数据的概率
p_val_high = multivariate_gaussian(X_val_high, mu_high, var_high)

# 找到最佳阈值
epsilon_high, F1_high = select_threshold(y_val_high, p_val_high)

print('使用交叉验证找到的最佳阈值: %e'% epsilon_high)
print('交叉验证集上的最佳F1值:  %f'% F1_high)
print('# 发现的异常数据数： %d'% sum(p_high < epsilon_high))

使用交叉验证找到的最佳阈值: 1.377229e-18
交叉验证集上的最佳F1值:  0.615385
# 发现的异常数据数： 117