【cutlass】cuTe layout操作

简介

cuTe提供了对Layout操作的算法，可以混合执行来构建更复杂的Layout操作，比如在其他layout之间切分和平铺layout

在host或者device上打印cuTe

cuTe的打印函数可以在host和device端打印。cute::print 重载了几乎所有 CuTe 类型，包括指针、Layout、形状、步幅和张量，thread0() 函数仅对内核的全局线程 0 返回 true，打印 CuTe 对象的典型习惯用法是仅在块 0 的线程 0 上打印。

if (thread0()) {
  print(some_cute_object);
}

有些算法在不同的threads或者blocks上执行不同的算法，为了在非零thread或者block上打印，需要加入一些在“cute/util/debug.hpp”中的debug单元。但是需要在使用之前需要判断“bool thread(int tid, int bid)”，只有在true的时候才可以使用。有的cuTe类型有特殊的打印函数可以使用不同的输出形式。它有一个采用rank-2 matrix layout 和 thread layout 重载，thread layout 是一个包含thread 和value 之间映射的表格。如果想打印latex格式，需要使用cute::print函数。

基本类型

Tuple

CuTe以tuple为启示，tuple是由零个或多个元素组成的有限有序列表。cuTe在device上也设计了"cute::tuple"，其行为与std::tuple类似但是为了简化对模板参数进行了限制。

IntTuple

然后cuTe定义了一个IntTuple作为一个整数或者一个IntTuple的Tuple类型。这个递归定义允许我们构建任意嵌套的布局。因此，以下任何一个都是IntTuple的有效模板参数：

“Run-time integers” (或者 “static integers”)只是像“int”或“size_t”这样的普通整数类型。
”Compile-time integers" 或者cuTe定义的子类，比如Int。这些类型都有一个共同点，即值是在类型本身中编码的（作为公共的“static constexpr value”成员）。CuTe将别名_1、_2、_3等定义为Int<1>、Int<2>、 Int<3>等类型。
带有任何模板参数的IntTuple
cuTe将IntTuple服用做很多不同的事情，包括Shape, Stride, Step和Coord。

Layout

Layout是一种tuple：(Shape, Stride)。从语义上讲，它实现了从“逻辑”形状（多维）索引到数组中的“物理”一维索引的映射。这里是一个具有静态步幅（3，1）的2x3阵列的示例：

Layout layout = make_layout(make_shape (_2{}, _3{}),
                            make_stride(_3{}, _1{}));
print_layout(layout);
for (int i = 0; i < size(layout); ++i) {
  print(layout(i));
  print(", ");
}
print("\n");
print(layout(1, 1));
print("\n");

输出结果（stride的意义可以参照 https://blog.csdn.net/qq_33146555/article/details/130551201），其中下划线标点符号“_”是Underscore的一个常量实例。它的作用类似于Python或Fortran数组切片中的“：”（冒号标点符号）：

(_2,_3):(_3,_1)
      0   1   2
    +---+---+---+
 0  | 0 | 1 | 2 |
    +---+---+---+
 1  | 3 | 4 | 5 |
    +---+---+---+
0, 3, 1, 4, 2, 5,
4

Tile

Tile不是Layout，而是Layout或者Tiles或者Underscores的一个tuple.下面讨论的代数Layout操作是在“Layout”上定义的，但“Tile”允许这些操作递归并应用于给定Layout的子Layout或特定模式。这些被称为按模式操作。

Layout的定义和运算

Layout是从整数（逻辑一维坐标）到整数（一维索引）的函数

上述打印示例中的“for”循环显示了CuTe如何用逻辑2-D坐标的column-major layout识别1-D坐标。从“i=0”到“size（Layout）”（即6）进行迭代，并用单个整数坐标“i”索引到我们的Layout中，以column-major 的方式遍历Layout，即使这是row-major的Layout。您可以从“for”循环（0，3，1，4，2，5）的输出中看到这一点。CuTe将该索引“i”称为“1-D坐标”，而“自然坐标”则是logical 2-D坐标。
如果您熟悉C++23的功能“mdspan”，这是“mdspan"布局映射”和CuTe“布局”之间的一个重要区别。“mdspan” Layout映射是单向的：它们总是采用多维逻辑坐标，并返回一个整数偏移量。根据步幅，偏移可以跳过物理1-D阵列的元素。因此，“mdspan”的偏移量与上面“for”循环中的一维逻辑坐标“i”的含义并不相同。您可以使用一维逻辑坐标在任何CuTe “Layout”上正确迭代。“mdspan” 没有一维逻辑坐标的概念。

Rank, depth, size, cosize

Rank: Layout型状的tuple尺寸
Depth: Layout形状的深度。单个整数的深度为0。元组的深度为1+其组件的最大深度。
Size: 形状的大小；函数的域的大小。这是Layout形状中所有范围的乘积。
Cosize: 函数共域的大小（不一定是范围）；对于Layout A，A(size(A) - 1) +1。（这里，我们使用size(A) - 1作为一维逻辑坐标输入。）

Layout 兼容

如果布局A和布局B的形状是兼容的，那么它们就是兼容的。如果A的任何自然坐标也是B的有效坐标，则形状A与形状B兼容。

Flatten

“Flatten”操作“un-nest”可能嵌套的Layout。例如：

Layout layout = Layout<Shape <Shape <_4, _3>, _1>,
                     Stride<Stride<_3, _1>, _0>>{};
Layout flat_layout = flatten(layout);

展平后的结果是：

Layout<Shape<_4, _3, _1>, Stride<_3, _1, _0>>

Layout layout = Layout<Shape <_4, Shape <_4,  _2>>,
                     Stride<_4, Stride<_1, _16>>>{};
Layout flat_layout = flatten(layout);

展平后的结果是：

Layout<Shape<_4, _4, _2>, Stride<_4, _1, _16>>

分层布局和平坦化使我们能够将tensor重新解释为matrix、matrix为vector、vector为matrices等。这使我们能够通过将收缩模式组合为单个模式，并根据需要组合A、B、C和“batch”模式，以达到所需的形式，将任意张量收缩实现为批处理矩阵乘法。

Coalesce

“coalesce”操作首先使Layout展平，然后组合所有可能组合的模式，从模式0（最左边的模式）开始，向右移动。如果所有模式都可以组合，那么这将产生一个一维Layout，表示原始Layout访问的数组元素。
“combine”模式意味着什么？在上面的示例中，展平的Layout是（2，1，6）：（1，6，2）。

如果我们看最左边的两个模式，这只是一个长度为2、步长为1的向量。中间模式具有范围1，因此无论如何都不会观察到相应的步幅6。这就给我们留下了（2，6）：（1，2）。
中间结果（2，6）：（1，2）只是一个2 x 6列的主矩阵，它可以合并为长度为12和步长为1的向量。
更正式地说，“组合所有模式”意味着左折叠，其中组合两种模式的二进制运算有三种情况。
如果最左边的Layout是s1:d1，下一个Layout是1:d0，则合并为s1:d1。这概括了上面的步骤1。如果一个模式的范围为1，我们就无法观察到它的步幅，所以我们可以跳过该模式。
如果最左边的Layout是1:d1，而下一个Layout是s0:d0，则合并为s0:d0。同样，如果一个模式的范围为1，我们无法观察到它的步幅，所以我们可以跳过该模式。
如果最左边的Layout是s1:d1，而下一个Layout是s0:s1d1，则合并为s0s1:d1。这概括了上面的步骤2。可以称之为“注意列的主要Layout顺序”
例如，合并行主布局 (2,2) : (2,1)的结果是 (2,2) : (2,1)，相同的布局，因为以上三种情况都不适用。

Complement

Definition

Layout A相对于整数M的补码B满足以下性质:

$A$ 和 $B$ 是不相交的: 在A的范围内，对于所有的 $\neq 0$ ， $\neq B(x)$ .
B 是 有序的: 对于所有 $\{0, 1, \dots, size(B) - 1\}$ 中的 $x$ ， $\lt B(x)$ .
B 的界是 M: $\geq M / size(A)$ , 并且 $\leq floor(M / cosize(A)) * cosize(A)$ .

关于不相交：我们需要指定 $x\neq 0$ ，因为CuTe Layout是线性的。也就是说，如果域是非空的，则该范围始终包含零。
关于有序性质：CuTe Layout是分层stride，因此这意味着如果size(B)为非零，那么B的stride都是正的。

Examples

complement(4:1, 24) 是6:4.

结果是4:1的不相交，因此它必须具有至少4的步幅（因为它包括0，但必须跳过1、2、3）。
结果的大小为 $\geq 24/4=6$ 。（这加上步骤（1）意味着cosize至少为24。）
结果的cosize $\leq（24/4）*4=24$ 。（这加上步骤（2）意味着cosize是24。）
size为6、cosize为24的唯一一维Layout为6:4。

complement(6:4, 24) 是4:1.

4:1与6:4不相交，但对于任何s>0和d>20，s:d也是如此。
结果的大小为 $\geq24/6=4$ 。
结果的cosize $\leq（24/21）*21=21$ 。
stride不能大于20（否则（2）将与（3）相矛盾），因此必须小于4。
因此剩下4:1。

Composition

Layout是函数，所以Layout的组合就是函数的组合。组合 $A\circ B$ 的意思是“首先应用Layout B，然后将结果视为Layout A的一维逻辑坐标输入，并对其应用A” 通常，此组合可以表示为另一个Layout。

Rules for computing composition

CuTe都使用以下规则计算Composition。

$\circ B$ 的形状与B兼容。在函数组合中，最右边的函数定义了域。对于，这意味着B的任何有效坐标也可以用作 $\circ B$ .
连接：Layout 可以表示为其子Layout的连接。我们用括号表示连接： $B=（B_0，B_1，…）$ 。当给定零个或多个“layout”时，CuTe函数“make_layout”会连接它们。
组合是（左-）分布的，带有级联： $\circ B = A \circ (B_0, B_1, ...) = (A \circ B_0, A \circ B_1, ...)$ 。
“Base case”：对于具有整体形状和步长的布局 $A = a : b$ 和 $B = c : d$ ， $\circ B = R = c : (b * d)$ .
按模式组合：让 $\langle B, C \rangle$ （尖括号，而不是圆括号）表示两个布局B和C的元组，而不是它们的串联。设 $A=（A_0，A_1）$ 。然后， $\circ \langle B, C \rangle = (A_0, A_1) \circ \langle B, C \rangle = (A_0 \circ B, A_1 \circ C)$ 。

这允许组合独立地应用于 $A$ 的子层。

Examples: Reshape a vector into a matrix

本节给出两个Composition 示例。两者都以布局为 $20 : 2$ 的向量开始（也就是说，向量有20个元素，每个元素之间的步长为2）。他们用4 x 5矩阵布局组成这个矢量。这有效地将矢量“重塑”为矩阵。

Example 1

这描述了将向量 $20 : 2$ 解释为4 x 5列主矩阵。结果Layout的形状为 $（ 4, 5 ）$ ，因为在函数组合中，最右边的函数定义了域。Stride 是什么？

布局可以表示为其子布局的串联，因此 $(4, 5) : (1, 4)$ 是 $(4 : 1, 5 : 4)$ 。
组成是分布式的，所以 $\circ (4:1, 5:4)$ 就是 $\circ 4:1, 20:2 \circ 5:4)$ 。
$20:2\circ4:1$ 的形状为4（最右边的函数定义域），步长 $2=2\cdot1$ 。
$\circ 5:4$ 具有形状5和步长 $8=2\cdot4$ 。
结果： (4:2, 5:8)，串联为(4,5) : (2,8)。

Example 2

$\circ (4,5) : (5,1)$ .
这描述了将向量20:2解释为4 x 5行主矩阵。与之前一样，生成的Layout具有形状 $（ 4, 5 ）$ 。Stride是什么？

通过去连锁， $(4, 5) : (5, 1)$ 是 $(4 : 5, 5 : 1)$ 。
合成是分配的，所以 $\circ (4:5, 5:1)$ 就是 $\circ 4:5, 20:2 \circ 5:1)$ 。
$20:2\circ4:5$ 的形状为 $4$ ，步长为 $\cdot 5$ 。
$20:2\circ5:1$ 具有形状 $5$ 和步长 $\cdot 1$ 。
结果：(4:10, 5:2)，串联为(4,5) : (10,2)。

Example: Reshape a matrix into another matrix

Composition $\circ (4,5):(1,4))$ 表示将布局为(20,2):(16:4)的矩阵以列为主的方式重塑为4 x 5矩阵。

通过去连锁， $(4, 5) : (1, 4)$ 是 $(4 : 1, 5 : 4)$ 。
组成是分配的，所以 $\circ (4:1, 5:4)$ 是 $\circ 4:1, (20,2):(16,4) \circ 5:4)$ 。
$\circ 4:1$ 具有形状 $4$ 和Stride $16$ 。（4:1表示选取(20,2):(16,4)的前4个连续元素。这些元素沿着Layout的第0列（最左边的模式）向下延伸，其Stride为16。）
$\circ 5:4$ 具有形状 $5$ 和Stride $64=4\cdot 16$ 。
结果： $(4 : 16, 5 : 64)$ ，通过串联为 $(4, 5) : (16, 64)$ 。

如果我们使用编译时的形状和步幅，我们就可以得到CuTe的确切结果。以下C++代码打印（_4，_5）：（_16，_64）

using namespace cute;
auto a = make_layout(make_shape(Int<20>{}, _2{}), make_stride(_16{}, _4{}));
auto b = make_layout(make_shape(     _4{}, _5{}), make_stride( _1{}, _4{}));
auto c = composition(a, b);
printf("\n");
print(c);

如果我们使用运行时整数，结果可能会不同（但在数学上是相同的）。以下C++代码打印（（4,1），（5,1））：（（16,4），（64,4））

using namespace cute;
auto a = make_layout(make_shape(20, 2), make_stride(16, 4));
auto b = make_layout(make_shape( 4, 5), make_stride( 1, 4));
auto c = composition(a, b);
printf("\n");
print(c);

((4,1),(5,1)) : ((16,4),(64,4)) 实际上与(4,5) : (16,64)的Layout相同，因为形状中的1不会影响Layout（作为从一个整数到一个整数的数学函数）。CuTe选择不尽可能多地使用运行时值来简化Layout计算，因为涉及运行时值的简化会产生运行时成本。

Product

CuTe包括四种不同的Layout Product:

logical_product
blocked_product
raked_product
tiled_product
logical_product（A，B）导致LayoutB的每个元素都被LayoutA的“副本”所取代。其他三种Product提供了这种方法的变体。

Example: Tiled matrix

假设我想设计一个由row-major中的3 x 4个tile组成的matrix，其中每个tile是2 x 2列的column-major matrix。每块tile的Layout有形状（2,2）和stride（1,2）。` matrix_of_tiles '的Layout有形状（3，4）和阶梯（4，1）。

Blocked product: the intuitive tiling

如果我用手推断出平铺矩阵的Layout应该是什么，它会是这样的：

	(0,0)	(1,0)	(0,1)	(1,1)	(0,2)	(1,2)	(0,3)	(1,3)
(0,0)	0	2	4	6	8	10	12	14
(1,0)	1	3	5	7	9	11	13	15
(0,1)	16	18	20	22	24	26	28	30
(1,1)	17	19	21	23	25	27	29	31
(0,2)	32	34	36	38	40	42	44	46
(1,2)	33	35	37	39	41	43	45	47

行和列标签使用1-D逻辑坐标和2-D列主坐标的等价性。每一对中的左索引是tile的行和列坐标，而每一对的右索引是行和列的坐标。tile矩阵的列坐标。得到的Layout具有Shape ((2, 3), (2, 4)) 和 Stride ((1, 16), (2, 4))，并且第二种模式可以合并。Shape ((2, 3), (2, 4))是分层的，但它仍然是rank-2，并且可以如上所述以2D绘制。请注意tile的行模式如何保留为产品的行模式的一部分，tile的列模式如何保留产品的列模式。上面的Layout是“blocked_product（tile，matrix_of_tiles）”生成的。blocked product 的一个关键用例是在矩阵上“tiling”一个“atom”（与硬件功能相关的一些tile）。

Layout tile            = Layout<Shape <_2,_2>,
                                Stride<_1,_2>>{};
Layout matrix_of_tiles = Layout<Shape <_3,_4>,
                                Stride<_4,_1>>{};

print_layout(blocked_product(tile, matrix_of_tiles));

Logical product

逻辑乘积logical_product（tile，matrix_of_tiles）产生Shape ((2, 2), (3, 4))和Stride ((1, 2), (16, 4))。

	(0,0)	(1,0)	(2,0)	(0,1)	(1,1)	(2,1)	(0,2)	(1,2)	(2,2)	(0,3)	(1,3)	(2,3)
(0,0)	0	16	32	4	20	36	8	24	40	12	28	44
(1,0)	1	17	33	5	21	37	9	25	41	13	29	45
(0,1)	2	18	34	6	22	38	10	26	42	14	30	46
(1,1)	3	19	35	7	23	39	11	27	43	15	31	47

请注意tile如何出现在最左边的列中，并在每列中以与tile矩阵相同的顺序进行复制。也就是说，可以通过结果的第一模式对tile进行索引，并且可以通过第二模式对tile矩阵进行索引。

Layout tile            = Layout<Shape <_2,_2>,
                                Stride<_1,_2>>{};
Layout matrix_of_tiles = Layout<Shape <_3,_4>,
                                Stride<_4,_1>>{};

print_layout(logical_product(tile, matrix_of_tiles));

Raked product

raked_product(tile, matrix_of_tiles)的结果是Shape ((3, 2), (4, 2)) 和 Stride ((16, 1), (4, 2))。

	(0,0)	(1,0)	(2,0)	(3,0)	(0,1)	(1,1)	(2,1)	(3,1)
(0,0)	0	4	8	12	2	6	10	14
(1,0)	16	20	24	28	18	22	26	30
(2,0)	32	36	40	44	34	38	42	46
(0,1)	1	5	9	13	3	7	11	15
(1,1)	17	21	25	29	19	23	27	31
(2,1)	33	37	41	45	35	39	43	47

tile现在与tile的另一个3x4矩阵interleave或“ranked”，而不是显示为block。其他参考文献称之为“循环分布”。如果你曾经使用过ScaLAPACK，这可能看起来很熟悉。它表示在2x2“过程网格"中的4个过程上的6 x 8矩阵的二维块循环分布，可以参考：“The Two-dimensional Block-Cyclic Distribution” 和 “Local Storage Scheme and Block-Cyclic Mapping”
通常，“logical_product”和这些变体可以产生任何interleaving，包括阻塞、循环、按模式阻塞/循环以及没有通用名称的中间交织。

Layout tile            = Layout<Shape <_2,_2>,
                                Stride<_1,_2>>{};
Layout matrix_of_tiles = Layout<Shape <_3,_4>,
                                Stride<_4,_1>>{};

print_layout(raked_product(tile, matrix_of_tiles));

Division

上一节介绍了Layout product，它们在另一个Layout上复制一个Layout。本节介绍Layout Division。将Layout划分为组件的函数作为tiling和partitioning Layout 的基础非常有用。例如，考虑将向量折叠成矩阵。我们可以想象一种称为“logical_diff”的运算，

Layout vec = Layout<_16,_3>{};           //  16 : 3
Layout col = Layout< _4,_1>{};           //   4 : 1
Layout mat = logical_divide(vec, col);   // (4,4) : (3,12)

它将向量的前4个元素“带入”第一种模式，并将“其余元素”留在第二种模式。这是“vec”中数据的column-major矩阵视图。如果我们想要一个row-major矩阵视图怎么办？

Layout vec = Layout<_16,_3>{};           //  16 : 3
Layout col = Layout< _4,_4>{};           //   4 : 4
Layout mat = logical_divide(vec, col);   // (4,4) : (12,3)

现在，向量的每四个元素都处于第一种模式，其余元素处于第二种模式。多维分层索引使我们可以将此操作扩展到任何“分割”矢量的布局。

Layout vec = Layout<_16,_3>{};           //  16 : 3
Layout col = Layout< _4,_2>{};           //   4 : 2
Layout mat = logical_divide(vec, col);   // (4,(2,2)) : (6,(3,24))

Layout vec = Layout<_16,_3>{};           //  16 : 3
Layout col = Layout<Shape <_2,_2>,
                    Stride<_4,_1>>{};    // (2,2) : (4,1)
Layout mat = logical_divide(vec, col);   // ((2,2),(2,2)) : ((12,3),(6,24))

上面所有的例子都产生了一个4x4矩阵，可以像普通的4x4矩阵一样进行索引和处理，但每个矩阵都有不同的底层Layout。因此，我们的算法可以使用逻辑坐标编写，而无需解决每个Layout所需的详细索引。CuTe包括3种不同类型的Layout划分操作：

logical_divide
zipped_divide
tiled_divide

Logical divide

Example worked in detail

Layout a = make_layout(24, 2);
Layout b = make_layout( 4, 2);
Layout c = logical_divide(a, b);

逻辑除法产生一个秩-2的“Layout”，其中模式0（最左边的模式）对应于除数“b”，模式1（最右边的模式）相应于“余数”。直观地说，24除以4的余数是6，所以我们知道模式1有6个元素。我们只是还不知道它的形状。
CuTe将logical_divide(a, b)定义为composition(a, make_layout(b, complement(b, size(a))))。这里，size(a)是24。直观地说，complement(b, 24)的意思是“余数”，即将b应用于0，1，2， $\dots$ ，23后剩下的余数。Layout 4:2的意思是“以偶数索引取4个元素。”下表覆盖了补码的共域0，1， $\dots$ ，23上4:2的范围。

Range of 4:2	0		2		4		6
Codomain	0	1	2	3	4	5	6	7	8	9	$\dots$	23

Layout是线性的，因此它们的范围必须包括零。因此，4:2相对于24的补码是一种布局，其范围

包括零；
不包括4:2范围内的任何其他元素（即满足不相交性质；见上文）;
包括尽可能多的0，1， $\dots$ ，23（从而形成4:2相对于24的“余数”）。

直觉上，补码的范围必须是这样的：0，1，8，9，16，17。将对生成的Layout进行排序。它的大小为6，cosize为18，因此它满足有界性质（见上文）。这是布局（2，3）：（1，8）。这从这种对补码的直观理解到知道如何直接计算补码超出了本教程这一部分的范围。）下表显示了4:2及其补码(2, 3) : (1, 8):

Range of 4:2	0		2		4		6
Codomain	0	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17	$\dots$	23
—	—	—	—	—	—	—	—	—	—	—	—	—	—	—	—	—	—	—	—	—
Range of complement	0	1							8	9							16	17

现在我们知道，logical_divide(24:2, 4:2)是composition(24:2, make_layout(4:2, (2,3):(1,8)))。两个Layout的组合具有第二（最右边）Layout的形状，因此得到的形状是(4, (2, 3))。我们看到，最左边的模式4对应于除数4:2，而最右边的模式(2, 3)描述了原始形状24的“遗留”部分。
Stride是什么？我们可以从最左边的模式开始。4:2取24:2的每一个其他元素（偶数元素）。这是第二步，跨过第二步。由此产生的步幅为4。类似地，24:2的步幅2是最右侧模式的两个步幅的两倍。得到的布局是(4, (2, 3)) : (4, (2, 16))。

Tiling example

假设我有来自Raked Product部分的6 x 8矩阵，并且想要“收集”“tile”，将Raked Product变成Blocked Product。要做到这一点，我们希望从列中收集两个元素并保留其余元素，然后从行中收集两种元素并保留剩余元素。因此，我们希望将“logical_diff”独立应用于行和列，以便检索适当的元素。在代码中，我们从Raked Product部分的结果中复制Layout，然后在要收集的行和列中指定元素。

Layout raked_prod = Layout<Shape <Shape < _3,_2>,Shape <_4,_2>>,
                           Stride<Stride<_16,_1>,Stride<_4,_2>>>{};
Tile   subtile    = make_tile(Layout<_2,_3>{},    // Gather elements 2 : 3 from mode 0
                              Layout<_2,_4>{});   // Gather elements 2 : 4 from mode 1

print_layout(logical_divide(raked_prod, subtile));

	(0,0)	(1,0)	(0,1)	(1,1)	(0,2)	(1,2)	(0,3)	(1,3)
(0,0)	0	2	4	6	8	10	12	14
(1,0)	1	3	5	7	9	11	13	15
(0,1)	16	18	20	22	24	26	28	30
(1,1)	17	19	21	23	25	27	29	31
(0,2)	32	34	36	38	40	42	44	46
(1,2)	33	35	37	39	41	43	45	47

Zipped divide

“zipped_dive”函数应用“logical_diff”，然后将“子文件”聚集到单个模式中，将“其余文件”聚集在单个模式中。

Layout raked_prod = Layout<Shape <Shape < _3,_2>,Shape <_4,_2>>,
                           Stride<Stride<_16,_1>,Stride<_4,_2>>>{};
Tile   subtile    = make_tile(Layout<_2,_3>{},    // Gather elements 2 : 3 from mode 0
                              Layout<_2,_4>{});   // Gather elements 2 : 4 from mode 1

print_layout(zipped_divide(raked_prod, subtile));

例如，如果我们在上面的例子中应用“zipped_dive”而不是“logical_diffe”，那么我们得到的结果

	(0,0)	(1,0)	(2,0)	(0,1)	(1,1)	(2,1)	(0,2)	(1,2)	(2,2)	(0,3)	(1,3)	(2,3)
(0,0)	0	16	32	4	20	36	8	24	40	12	28	44
(1,0)	1	17	33	5	21	37	9	25	41	13	29	45
(0,1)	2	18	34	6	22	38	10	26	42	14	30	46
(1,1)	3	19	35	7	23	39	11	27	43	15	31	47

这与Logical Product部分中的结果是相同的Layout。也就是说，第一种模式是我们的原始tile（可以解释为2x2矩阵本身），第二种模式是其在raked layout中的logical layout。

More Examples of Divide

为了简洁起见，shape可以与logical_divide和tiled_divide一起使用，以快速拆分和平铺张量的模式。例如，这个C++代码

Layout layout     = Layout<Shape <_12, _32,_6>,
                           Stride< _1,_128,_0>>{};
Shape  tile_shape = make_shape(_4{},_8{});
Layout logical_divided_tile = logical_divide(layout, tile_shape);
Layout zipped_divided_tile  =  zipped_divide(layout, tile_shape);

print("layout               :  "); print(layout);               print("\n");
print("tile_shape           :  "); print(tile_shape);           print("\n");
print("logical_divided_tile :  "); print(logical_divided_tile); print("\n");
print("zipped_divided_tile  :  "); print(zipped_divided_tile);  print("\n\n");

产生的输出是：

full_layout          :  (_12,_32,_6):(_1,_128,_0)
tile_shape           :  (_4,_8)
logical_divided_tile :  ((_4,_3),(_8,_4),_6):((_1,_4),(_128,_1024),_0)
zipped_divided_tile  :  ((_4,_8),(_3,_4,_6)):((_1,_128),(_4,_1024,_0))

full_layout          :  (_12,(_4,_8),_6):(_1,(_32,_512),_0)
tile_shape           :  (_4,_8)
logical_divided_tile :  ((_4,_3),((_4,_2),_4),_6):((_1,_4),((_32,_512),_1024),_0)
zipped_divided_tile  :  ((_4,(_4,_2)),(_3,_4,_6)):((_1,(_32,_512)),(_4,_1024,_0))

Layout layout = make_layout(Shape<_8,_8>{},
                            Stride<_8,_1>{});
Layout tile = make_tile(make_layout(Shape<_4>{}),
                        make_layout(Shape<_2>{}));
print("layout: ");
print_layout(layout);
print("\n");
print("tile: ");
print(tile);
print("\n");
print("logical_divide: ");
print_layout(logical_divide(layout, tile));
print("zipped_divide: ");
print_layout(zipped_divide(layout, tile));

的结果是
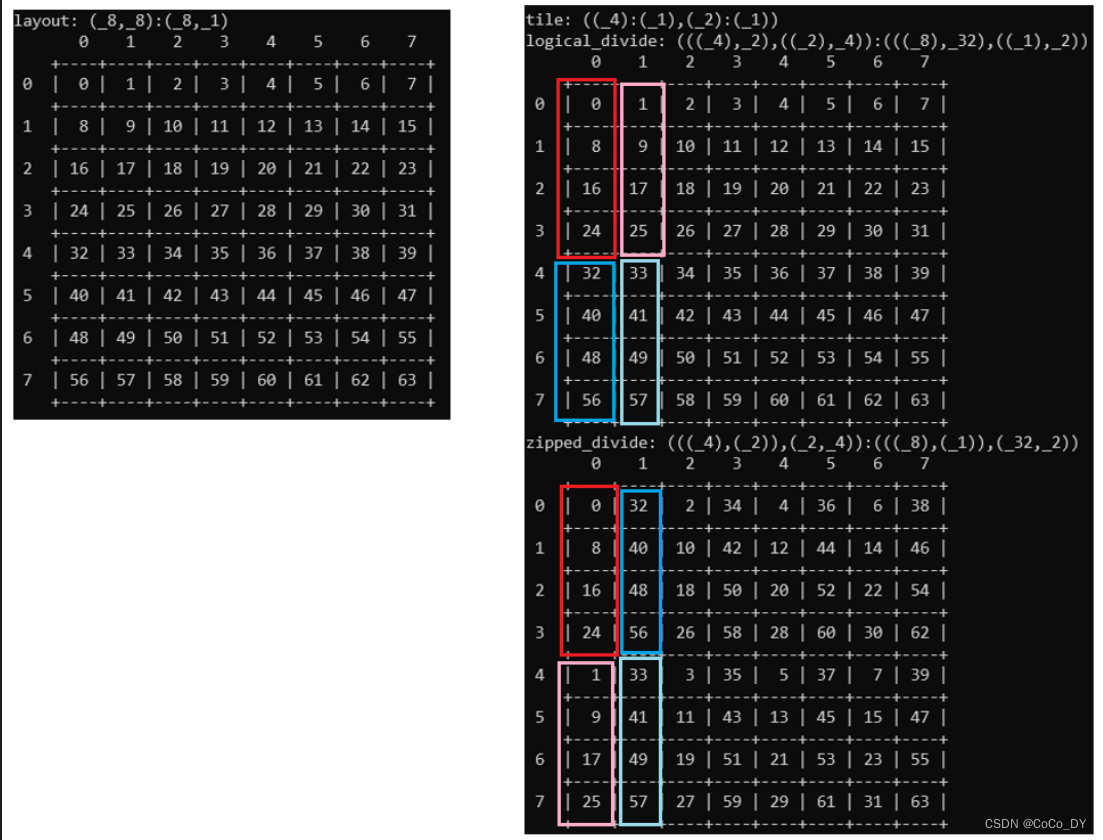
在这里插入图片描述

Layout layout = make_layout(Shape<_8,_8>{},
                            Stride<_8,_1>{});
Layout tile = make_tile(make_layout(Shape<_2>{}),
                        make_layout(Shape<_4>{}));
print("layout: ");
print_layout(layout);
print("\n");
print("tile: ");
print(tile);
print("\n");
print("logical_divide: ");
print_layout(logical_divide(layout, tile));
print("zipped_divide: ");
print_layout(zipped_divide(layout, tile));

的结果是
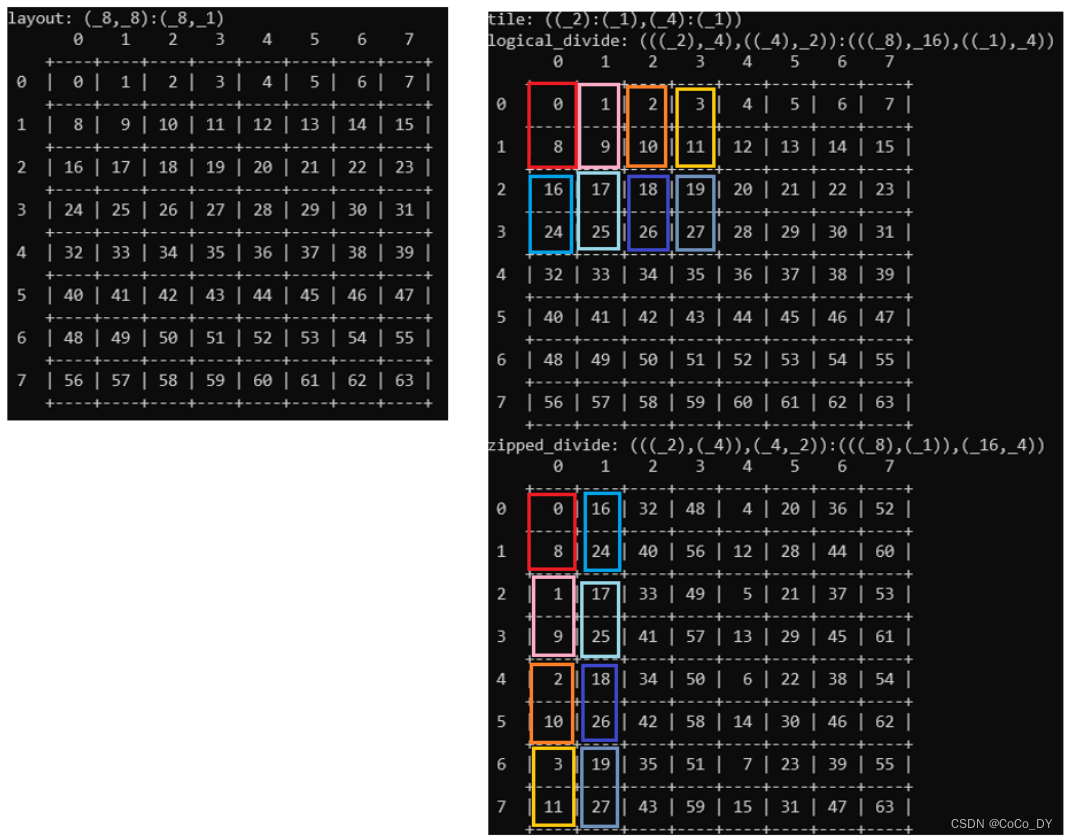
在这里插入图片描述

Tiled divide

tiled_divide函数的工作原理与zipped_divide类似，只是它取消打包第二种模式。例如，当您有一个Tile来描述特定操作的所有元素，并且希望将这些元素聚集在一起，但在原始布局中保留这些平铺的逻辑形状时，这很有用。也就是说，

Layout Shape : (M, N, L, ...)
Tile Shape   : <M', N'>
Tiled Result : ((M', N'), m, n, L, ...)

其中m 是M / M' 同时 n 是 N / N'。我们可以将m看作M中Tile的个数”，将n看作N中Tile的数目”。这种操作风格在应用MMA Atoms和Copy Atoms时很常见。