文章目录
- 霍夫变换原理
- 当点都在y轴上时,用y=kx+b形式是无法求出参数空间中的交点,也就是累计都一样。所以就用极坐标来表示参数空间。
- 公式求证
- 过程
霍夫变换原理
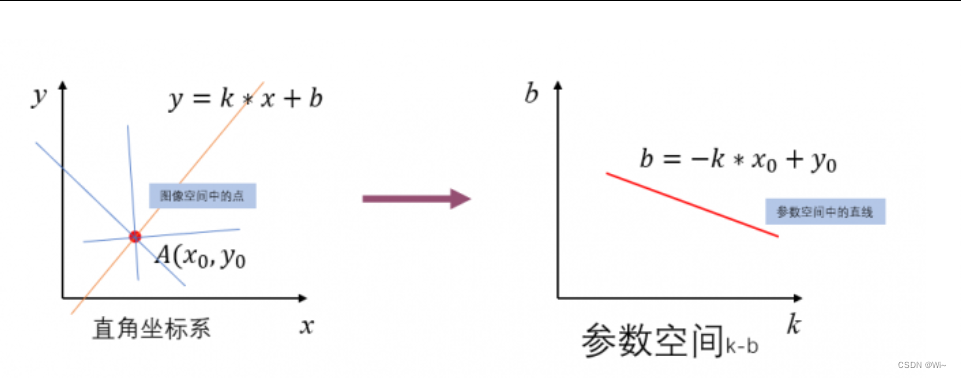
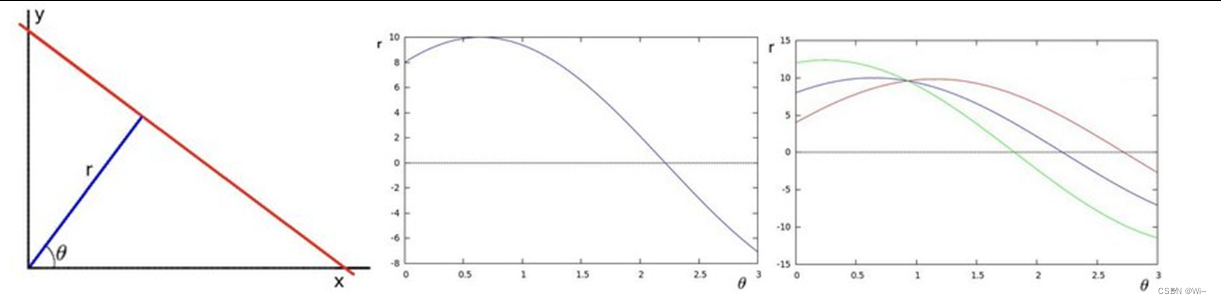
当点都在y轴上时,用y=kx+b形式是无法求出参数空间中的交点,也就是累计都一样。所以就用极坐标来表示参数空间。
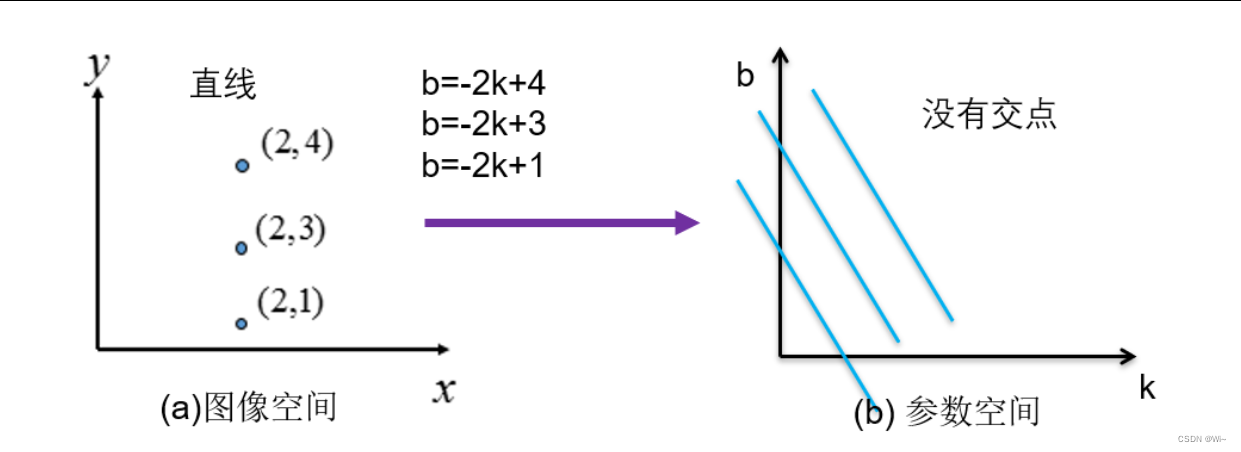

公式求证
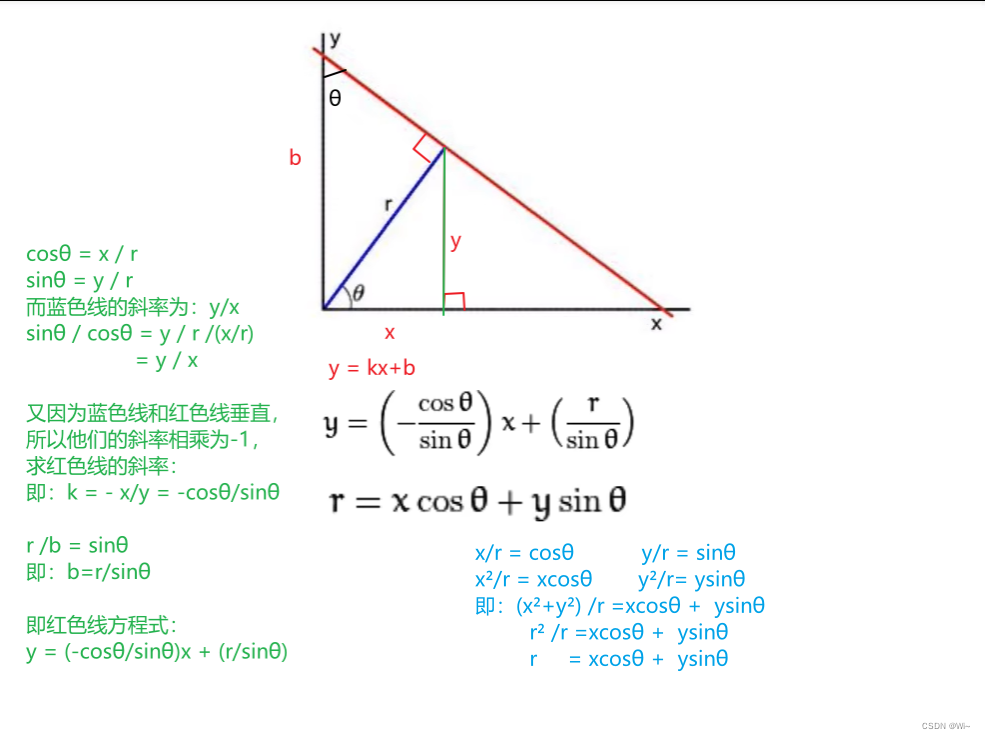
cosθ = x / r
sinθ = y / r
而蓝色线的斜率为:y/x
sinθ / cosθ = y / r /(x/r)
= y / x
又因为蓝色线和红色线垂直,
所以他们的斜率相乘为-1,
求红色线的斜率:
即:k = - x/y = -cosθ/sinθ
r /b = sinθ
即:b=r/sinθ
即红色线方程式:
y = (-cosθ/sinθ)x + (r/sinθ)
过程
霍夫变换是一种图像处理技术,可以用来检测出图像中的直线、圆等形状。
霍夫变换找直线的原理如下:
-
在笛卡尔坐标系中,一条直线可以用 y = mx + b 的形式表示,其中 m 是斜率,b 是截距。将直线用极坐标表示,可以得到:
rho = x * cos(theta) + y * sin(theta)
其中,rho 表示直线到坐标原点的距离,theta 表示直线与 x 轴的夹角。
-
对于图像中的每个点,遍历所有可能的 rho 和 theta 组合,并在霍夫空间中进行累加。
-
在霍夫空间中,如果有多个点在同一直线上,那么它们对应的 rho 和 theta 组合的累加值会比较高,可以通过设置一个阈值来确定直线。
-
在霍夫空间中,每个点对应的 rho 和 theta 组合对应着一条直线,可以通过取出累加值最高的几个点来确定图像中的直线。
-
霍夫直线检测的优缺点
优点:霍夫变换找直线的优点是能够检测出图像中的所有直线,不需要预先知道直线的位置和方向。Hough直线检测的优点是抗干扰能力强,对图像中直线的殘缺部分、噪声以及其它共存的非直线结构不敏感,能容忍特征边界描述中的间隙,并且相对不受图像噪声的影响。
缺点:Hough变换算法的特点导致其时间复杂度和空间复杂度都很高,并且在检测过程中只能确定直线方向,丢失了线段的长度信息。由于霍夫检测过程中进行了离散化,因此检测精度受参数离散间隔制约
以下是C++代码实现霍夫变换找直线的示例:
void HoughTransform(Mat& img, Mat& dst)
{
// 定义图像的宽和高
int width = img.cols;
int height = img.rows;
double rhoMax = sqrt(pow(width, 2) + pow(height, 2)); // 最大极径
int thetaMax = 180; // 最大极角
int accumHeight = (int)(rhoMax * 2 + 1); // 累加器高度
int accumWidth = thetaMax;// 累加器宽度
// 定义霍夫变换的参数空间的大小
Mat accum(accumHeight, accumWidth, CV_32SC1, Scalar(0)); // 累加器
int centerX = width / 2;
int centerY = height / 2;
for (int y = 0; y < height; ++y)
{
for (int x = 0; x < width; ++x)
{
if (img.at<uchar>(y, x) == 255)
{
for (int theta = 0; theta < thetaMax; ++theta)
{
double rho = (x - centerX) * cos(theta * CV_PI / 180) + (y - centerY) * sin(theta * CV_PI / 180); // 极径
int rhoIndex = (int)cvRound(rho + rhoMax);
accum.at<int>(rhoIndex, theta)++;
}
}
}
}
dst = Mat::zeros(height, width, CV_8UC1);
// 对每个参数进行遍历 找到霍夫变换参数空间中的峰值
for (int rhoIndex = 0; rhoIndex < accumHeight; ++rhoIndex)
{
for (int theta = 0; theta < thetaMax; ++theta)
{
// 如果当前参数对应的计数值大于等于阈值
if (accum.at<int>(rhoIndex, theta) > 150)
{
/*首先,我们将rhoIndex从数组索引值转换回霍夫空间中的极径rho。
这里需要注意,由于我们之前对rho进行了平移,所以在转换回来时,
我们需要将rhoMax再次减去以得到正确的极径值。*/
double rho = rhoIndex - rhoMax;
double a = cos(theta * CV_PI / 180);
double b = sin(theta * CV_PI / 180);
//转换原来x和y的实际像素坐标
double x = a * rho + centerX;
double y = b * rho + centerY;
//当一个直线角度不变的情况下,x 移动(-b),y也跟着移动a
//-b = sin() = x/r a = cos() = y/r 当r=1000 r*x/r =x r*y/r = y (x和-y的关系:比率不变) 也就是角度不变,坐标沿着同一角度的直线变化
Point pt1(cvRound(x + 1000 * (-b)), cvRound(y + 1000 * a));
Point pt2(cvRound(x - 1000 * (-b)), cvRound(y - 1000 * a));
//Point pt1(cvRound(x + 1000 * (b)), cvRound(y + 1000 * -a));
//Point pt2(cvRound(x - 1000 * (b)), cvRound(y - 1000 * -a));
line(dst, pt1, pt2, Scalar(255), 1, LINE_8);
}
}
}
}
上面代码centerX 有什么用意?
在霍夫变换中,我们需要将每个像素点的坐标转换为极坐标系下的极径和极角。由于极径的范围通常是从原点到图像边缘的最大距离,因此在计算极径时,我们需要将每个像素的坐标平移使其相对于图像中心而非左上角。
在代码中,centerX是图像宽度的一半,即图像中心点的x坐标。我们将每个像素的x坐标减去centerX,以将坐标系统平移到图像中心。
同样,centerY是图像高度的一半,即图像中心点的y坐标。我们将每个像素的y坐标减去centerY,以将坐标系统平移到图像中心。
这样做的目的是确保极径的计算基于图像中心而非左上角,从而使算法更加准确。
int rhoIndex = (int)(rho + rhoMax + 0.5); 这段代码什么意思
这段代码是将当前直线在霍夫空间中的极径rho转换为在accum数组中的索引值rhoIndex。
在霍夫空间中,极径的值通常是一个浮点数。为了在数组中保存极径的计数值,我们需要将它们转换为整数类型。因此,我们使用(int)将rho强制转换为整数类型。此外,我们需要将所有的极径值移动到正数范围内,以便在数组中使用。因此,我们添加一个常数rhoMax,该常数等于极径的最大值加上1,以将所有极径值移动到正数范围内。
最后,我们使用0.5来进行四舍五入,以确保将rho值正确地映射到rhoIndex上。这样可以避免由于浮点数的舍入误差而导致的不准确的索引值。
double rho = rhoIndex - rhoMax;
double a = cos(theta * CV_PI / 180);
double b = sin(theta * CV_PI / 180);
double x0 = a * rho + centerX;
double y0 = b * rho + centerY;
这段代码是将accum数组中的索引值转换回霍夫空间中的极坐标。
首先,我们将rhoIndex从数组索引值转换回霍夫空间中的极径rho。这里需要注意,由于我们之前对rho进行了平移,所以在转换回来时,我们需要将rhoMax再次减去以得到正确的极径值。
然后,我们将极角theta转换为弧度制,并计算出直线的参数a和b。这里需要注意,OpenCV中的三角函数接受的是弧度制而非角度制的参数,所以我们需要将theta转换为弧度制。
接下来,我们计算直线在笛卡尔坐标系下的截距x0和y0。这里的计算公式来自于霍夫变换中的极坐标到笛卡尔坐标的转换公式:
x = r cos(theta) + x0
y = r sin(theta) + y0
其中,x0和y0是直线在笛卡尔坐标系下的截距,theta是直线在霍夫空间中的极角,r是直线在霍夫空间中的极径。通过将r替换为计算得到的rho,我们可以将直线的极坐标转换为笛卡尔坐标。由于之前我们对坐标进行了平移,所以在计算x0和y0时,我们需要将它们还原回原始坐标系。
Point pt1(cvRound(x + 1000 * (-b)), cvRound(y + 1000 * a));
Point pt2(cvRound(x - 1000 * (-b)), cvRound(y - 1000 * a));
这段代码是用来在图像上绘制检测到的直线。
由于在霍夫空间中,直线的表示形式是(rho, theta),其中rho表示直线到图像中心的距离,theta表示直线与x轴的夹角,因此我们需要将它们转换为笛卡尔坐标系下的表示形式,即直线的两个端点坐标(x1, y1)和(x2, y2)。
对于一条直线,我们可以根据它在霍夫空间中的参数rho和theta,以及一个固定长度的线段来计算它在图像上的两个端点坐标。
具体地,我们首先计算线段的一个端点(x1, y1),其中x1和y1分别等于直线在笛卡尔坐标系下的截距(x0, y0)加上一个向量(-b, a),该向量的长度为1000。向量(-b, a)的长度可以控制我们在图像上绘制直线的长度。
然后,我们计算线段的另一个端点(x2, y2),其中x2和y2分别等于直线在笛卡尔坐标系下的截距(x0, y0)加上一个向量-(-b, a),该向量的长度同样为1000。注意,在计算x2和y2时,我们将向量-(-b, a)写成了(b, -a),因为-(-b, a)等于(b, -a)。
最后,我们使用OpenCV的cvRound函数将x1、y1、x2和y2四个值分别四舍五入为整数,以便在图像上绘制直线。然后,我们将x1和y1作为直线的起点,将x2和y2作为直线的终点,在图像上绘制一条直线。
为什么(-b, a)是向量?
(-b, a)是一个向量,它可以表示为一个有向线段,其起点为原点(0, 0),终点为点(-b, a)。
在这个问题中,(-b, a)被用来表示垂直于直线的向量。我们可以将这个向量添加到直线在笛卡尔坐标系下的截距点(x0, y0)上,从而得到直线上的另一个点(x2, y2)。
这个向量的长度为1000,可以用来控制绘制的直线的长度。在具体实现时,我们将这个向量的长度设置为1000个像素,因此直线的长度为1000个像素。




![读书笔记-《ON JAVA 中文版》-摘要17[第十七章 文件]](https://img-blog.csdnimg.cn/7913f53fd314422d8f612f3e3093d1b2.png)