图像边缘检测原理

1:

图像的边缘指的是图像中像素灰度值突然发生变化的区域，如果将图像的每一行像素和每一列像素都描述成一个关于灰度值的函数，那么图像的边缘对应在灰度值函数中是函数值突然变大的区域。函数值的变化趋势可以用函数的导数描述。当函数值突然变大时，导数也必然会变大，而函数值变化较为平缓区域，导数值也比较小，因此可以通过寻找导数值较大的区域去寻找函数中突然变化的区域，进而确定图像中的边缘位置。图5-27给出一张含有边缘的图像，图像每一行的像素灰度值变化可以用图中下方的曲线表示。

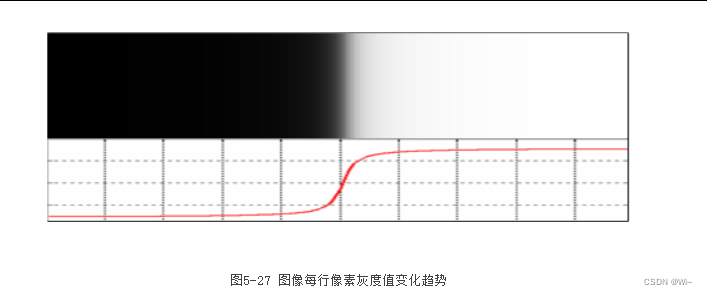
在这里插入图片描述

通过像素灰度值曲线可以看出图像边缘位于曲线变化最陡峭的区域，对灰度值曲线求取一阶导数可以得到图5-28中所示的曲线，通过曲线可以看出曲线的最大值区域就是图像中的边缘。
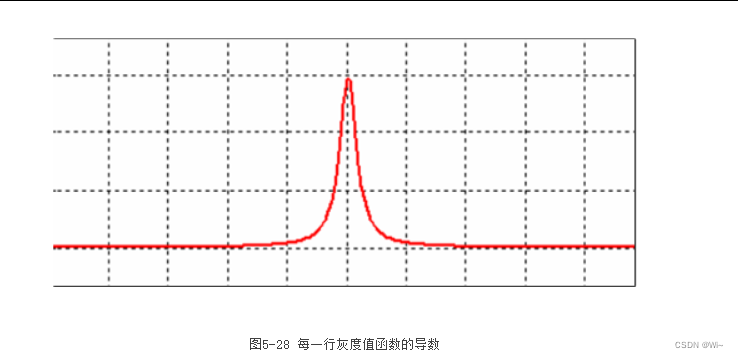
在这里插入图片描述

图像的边缘有可能是由高像素值变为低像素值，也有可能是由低像素值变成高像素值，通过式(5.13)和式(5.14)得到的正数值表示需要像素值突然由低变高，得到的负数值表示像素值由高到低，这两种都是图像的边缘，因此为了在图像中同时表示出这两种边缘信息，需要将计算的结果求取绝对值。

2:

数字图像的边缘检测在图像处理中起着十分重要的作用，十分简单又有效的方法就是微分算子，常见的微分算子包括：Sobel算子、Robert算子、Prewitt算子、Laplacian算子、Canny算子。

从名字也可以看出，微分算子，当然涉及到求导，为什么对图像进行求导就可以检测图像中的边缘呢？图像的边缘一般存在灰度变化强烈的地方，只有灰度变化的明显我们才可以从图像中清晰的看到没有一个物体的轮廓，要是一个图像灰度变化很均匀的话，整个图像就变得比较模糊。就如把一副图像均值滤波以后，图像变得模糊了。如何表示一个图像的灰度变化，当然是求导了，梯度值越大表示图像中灰度值变化越剧烈，越有可能是图像的边缘。图像求导包括一阶和二阶，二阶导数比一阶导数在细节方面处理的更好一点，但是也各有利弊，如含有噪声的图像就不适合二阶导，因为他会把图像中的噪声增强，所以需要先做平滑处理。

下面看一下在图像中一阶导和二阶导是怎么求的。在数学中一维函数的一阶导数的概念如下：
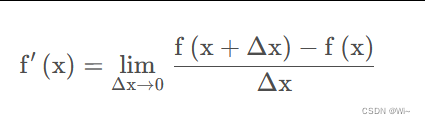
在这里插入图片描述

图像是一个二维的函数 f(x,y)，所以需要求偏微分：
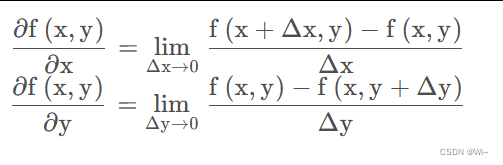
在这里插入图片描述

因为图像是离散的像素点，所以其中的 Δx、 Δ y 不能无限小，所以按照只能按照像素为单位， Δ x = 1， Δy=1 ；然后可以知道上面的微分方程就变成了如下的形式
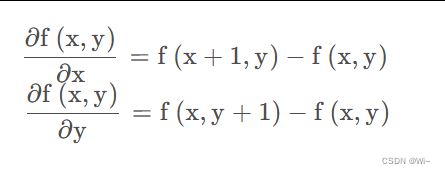
在这里插入图片描述

所以一副图像x方向和y方向的梯度就是连个相邻像素之间的差值。那么求整体的梯度公式就如下：
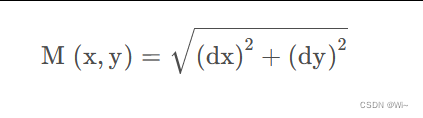
在这里插入图片描述

这样图像的一阶导就完事了，然后同样的，二阶导的推理如下：
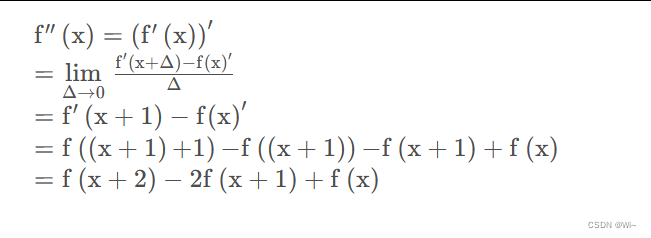
在这里插入图片描述

所以令 x = −1，就可以得到
在这里插入图片描述

整体图像的二阶导：
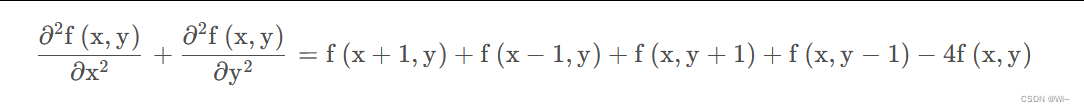
在这里插入图片描述

3:基本边缘检测算子

在介绍完滤波的知识后，学习基本边缘检测算法是一件很轻松的事情，因为边缘检测本质上就是一种滤波算法，区别在于滤波器的选择，滤波的规则是完全一致的

为了更好理解边缘检测算子，我们引入梯度(gradient)这一概念，梯度是人工智能(artificial intelligence)非常重要的一个概念，遍布机器学习、深度学习领域，学过微积分的同学应该知道一维函数的一阶微分基本定义为：

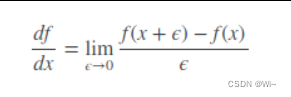
在这里插入图片描述

而我们刚才也提到了，图像的滤波一般是基于灰度图进行的，因此图像此时是二维的，因此我们在看一下二维函数的微分，即偏微分方程：
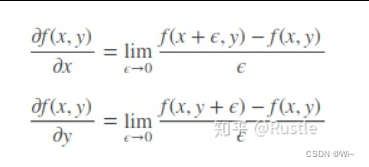
在这里插入图片描述

由上面的公式我们可以看到，图像梯度即当前所在像素点对于X轴、Y轴的偏导数，所以梯度在图像处理领域我们可以也理解为像素灰度值变化的速度，下面我们举一个简单的例子：
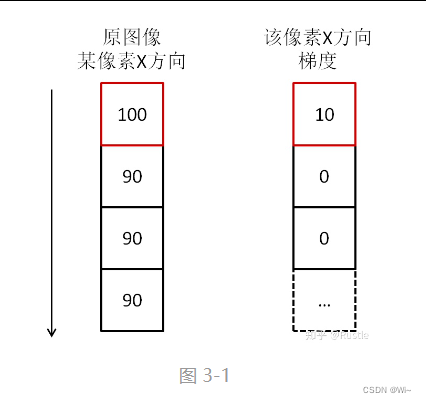
在这里插入图片描述

图中我们可以看到，100与90之间相差的灰度值为10，即当前像素点在X轴方向上的梯度为10，而其它点均为90，则求导后发现梯度全为0，因此我们可以发现在数字图像处理，因其像素性质的特殊性，微积分在图像处理表现的形式为计算当前像素点沿偏微分方向的差值，所以实际的应用是不需要用到求导的，只需进行简单的加减运算

而另一个概念梯度的模则表示f(x, y)，在其最大变化率方向上的单位距离所增加的量，即：
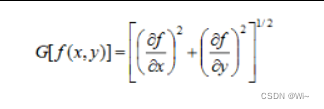
在这里插入图片描述

代码演示：

Mat img = imread("D:/OpenCV4.5.1/opencv/sources/doc/js_tutorials/js_assets/lena.jpg", IMREAD_GRAYSCALE);

	if (img.empty())
	{
		cout << "请确认图像文件名称是否正确" << endl;
		return -1;
	}

	// 创建边缘检测滤波器
	Mat kernel2 = (Mat_<float>(1, 3) << -1, 0, 1); // X方向边缘检测滤波器
	Mat kernel3 = (Mat_<float>(3, 1) << -1, 0, 1); // Y方向边缘检测滤波器

	Mat result1, result2, result3, result4, result5, result6;

	// 检测图像边缘

	// 以 [1 0 -1] 检测水平方向边缘
	filter2D(img, result2, CV_32F, kernel2);
	convertScaleAbs(result2, result2);

	// 以 [1 0 -1]' 检测由垂直方向边缘
	filter2D(img, result3, CV_32F, kernel3);
	convertScaleAbs(result3, result3);

	// 相加后整幅图像的边缘梯度
	result6 = result2 + result3;

	//先转换为浮点型，下面求平方开方会报错 类型不对
	result2.convertTo(result4, CV_32F);
	result3.convertTo(result5, CV_32F);

	// 求平方和再开方后整幅图像的边缘梯度
	pow(result4, 2.0, result4);
	pow(result5, 2.0, result5);
	sqrt(result4 + result5, result1);
	// 将 result1 归一化到 [0, 255] 范围内，不然直接显示 会超出255
	Mat result1_normalized;
	normalize(result1, result1_normalized, 0,  255, NORM_MINMAX, CV_8UC1);


	// 显示边缘检测结果
	imshow("X方向边缘", result2);
	imshow("Y方向边缘", result3);
	imshow("X+Y后整幅图像的边缘", result6);
	imshow("sqrt(X²+Y²)整幅图像的边缘", result1_normalized);

	waitKey(0);

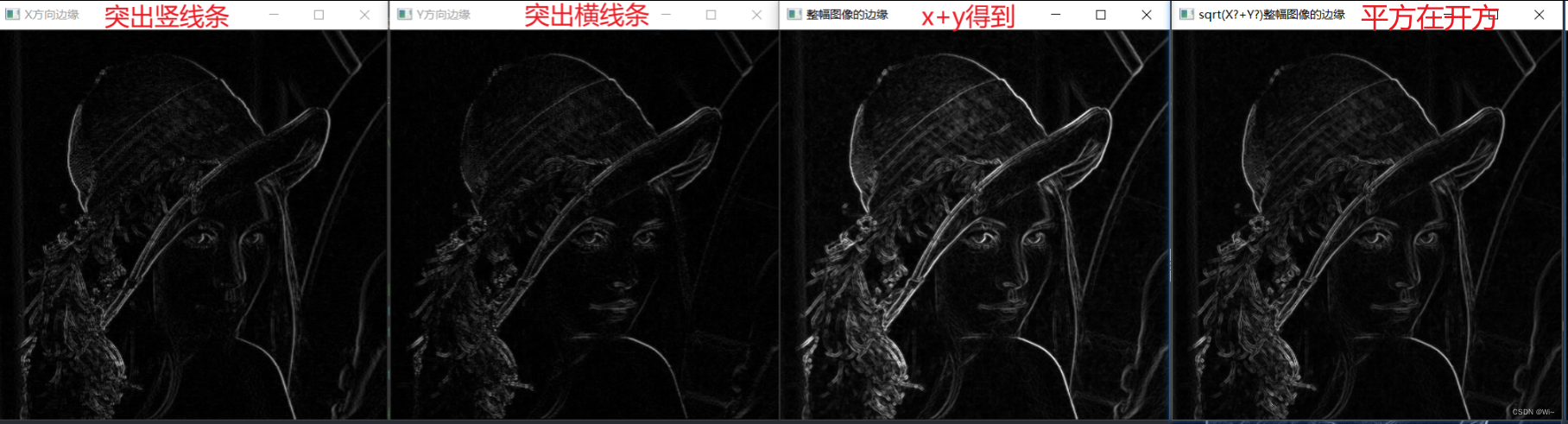
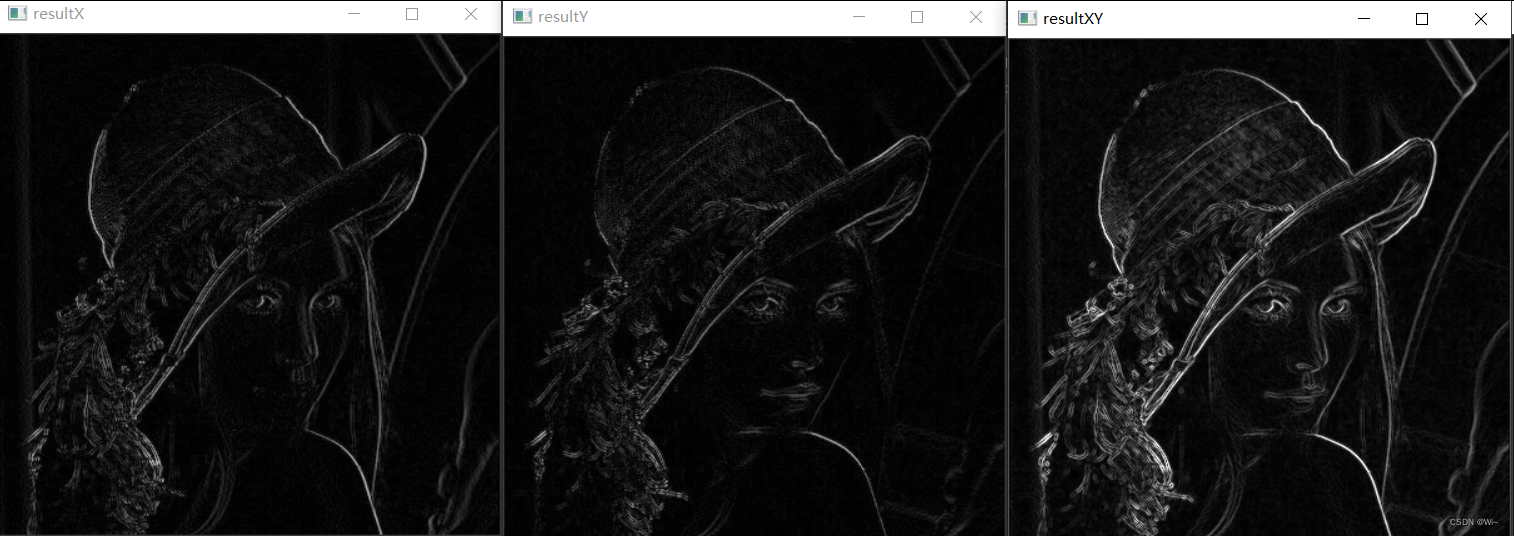
在这里插入图片描述

利用Sobel算子一阶和31卷积和13卷积实现上面一样的功能

    Mat img = imread("D:/OpenCV4.5.1/opencv/sources/doc/js_tutorials/js_assets/lena.jpg", IMREAD_GRAYSCALE);

	if (img.empty())
	{
		cout << "请确认图像文件名称是否正确" << endl;
		return -1;
	}

	Mat resultX, resultY, resultXY;

	//X方向一阶边缘
	Sobel(img, resultX, CV_16S, 1, 0, 1);
	convertScaleAbs(resultX, resultX);

	//Y方向一阶边缘
	Sobel(img, resultY, CV_16S, 0, 1, 1);
	convertScaleAbs(resultY, resultY);

	//整幅图像的一阶边缘
	resultXY = resultX + resultY;

	//显示图像
	imshow("resultX", resultX);
	imshow("resultY", resultY);
	imshow("resultXY", resultXY);