深度学习经典trick汇总

trick这个词或许有投机取巧的意味，但深度学习论文中出现的很多这个trick确实对模型更方面性能有所提高，而且它们中的很多还具有普适性，那么这种“trick“或许应该被叫做“技术”。

1. 权重衰减

$${\theta }_{t+1}=(1-\omega \alpha ){\theta }_t-\alpha {\nabla }_{{\theta }_t}L(x,{\theta }_t{)}^T\text{\hspace{1em}(1-1)}$$

(1-1)为引入权重衰减时参数更新公式，ω为权重衰减系数，α为学习率。可以直观的看出，引入权重衰减与不引入权重衰减相比，θ会有减小的倾向。通过推导可知在不引入动量的SGD优化器中，权重衰减等价于对权重L2正则化，详见笔记：[L2正则化与权重衰减]。

权重衰减实际上限制了权重的可行域，相当于降低了模型的复杂度，目前是防止模型过拟合的一种常用手段。

• **tips：**一般来说，ω取值越大，权重衰减越剧烈，模型拟合能力越差，易造成欠拟合，所以ω一般取较小的值（<=1e-3）。ω的取值也是一个需要不断调参的过程，让模型最终处于欠拟合与过拟合之间的状态。

2. Dropout层

Dropout（暂退）层的做法也十分好理解：在上一层输出后以一定概率随机屏蔽掉部分神经元（令其们输出为0）。
$$h^{{}^{\prime }}=\{\begin{array}{ll}0& 概率为p\\ \frac{h}{1-p}& 其他情况\end{array}\text{\hspace{1em}(2-1)}$$
由(2-1)，h为神经元原输出，h‘为暂退后输出。可见上一层输出经过Dropout层后，均值不变。（但方差变了）

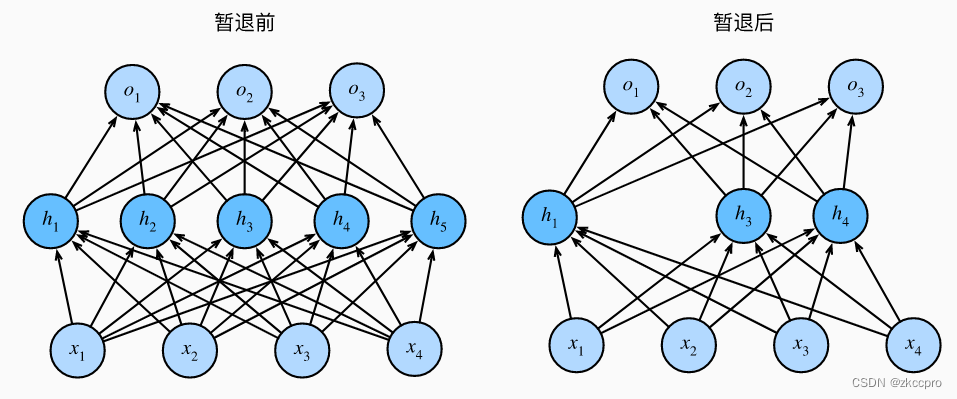
图1 暂退层的作用

这种方法更“粗暴”地降低了权重数量，降低了模型复杂度，当然可以【避免过拟合】，很好理解吧。

• tips：【暂退概率】是Dropout层唯一需要调整的超参数，以这个概率随机丢掉部分神经元。该值在(0,1)之间取值。经验取值在(0,0,5]之间，而且越靠近输入层暂退概率应该取值越小，以保留更多可能有价值的特征。

  需要注意一个事情，在前向传播的时候暂退层是【随机】丢弃一部分神经元。改变输出方差的同时也是输出变得不稳定，可能造成无法收敛或者loss震荡的情况，所以如果加入暂退层的网络出现loss震荡的情况就应该考虑减少或去掉暂退层。

3. 标准化层

标准化层一般是添加在隐藏层后的一种对其输出数据标准化处理的trick。我们已经知道输入数据需要标准化后才能输入网络，其实标准化也是一个道理。你想想，隐藏层有很多权重和输入数据做线性计算输出，再逐一对元素进行非线性计算，那怎么保证中间输出的数据仍然保证分布一致？中间数据分布不一致了后面网络的处理效果不就更差了？

所以，对于深层神经网络而言，标准化层是一个【保证模型拟合能力】的一种必要trick。

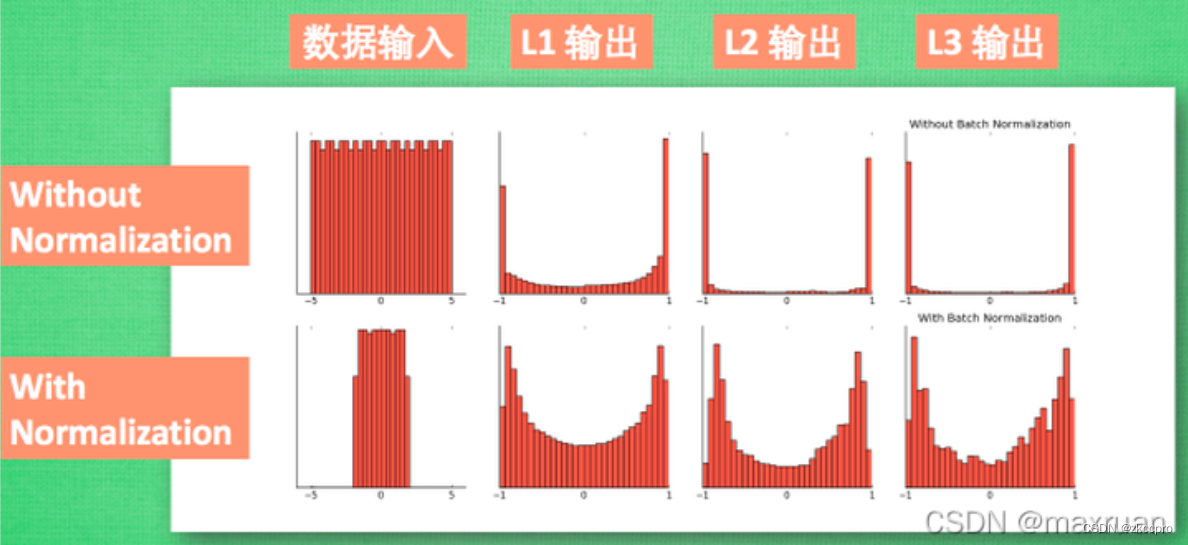
图2 标准化处理数据的作用

那么接下来的问题是，归一化层的设计是什么样的？下面看看归一化层的计算公式：
$$\begin{gathered} {\mu }_S=\frac{1}{m}\sum _{i=1}^m{x}_i \\ {\sigma }_S^2=\frac{1}{m}\sum _{i=1}^m(x_i-{\mu }_S{)}^2 \\ \widehat{x_i}=\frac{x_i-{\mu }_S}{\sqrt{{\sigma }_S^2+\xi }} \\ {y}_i=\gamma \widehat{x_i}+\beta \text{\hspace{1em}(3-1)} \end{gathered}$$
xi是输入数据，m是输入数据个数，yi是输出，γ β作为标准化层参数，S是数据标准化的域。

好理解吧，先算数据均值和方差，然后减均值 除以方差，再计算最终输出。这里重点解释两点：标准化层参数，和标准化域。

标准化层的参数可以作为整个网络的权重，加入梯度反向传播计算；也可以不作为网络权重，直接取常数，各种深度学习框架都对此细节有很好的支持。

而标准化域S有点不太好理解，标准化层有4种标准化域，下面这副图可以很好的说明它们的关系：

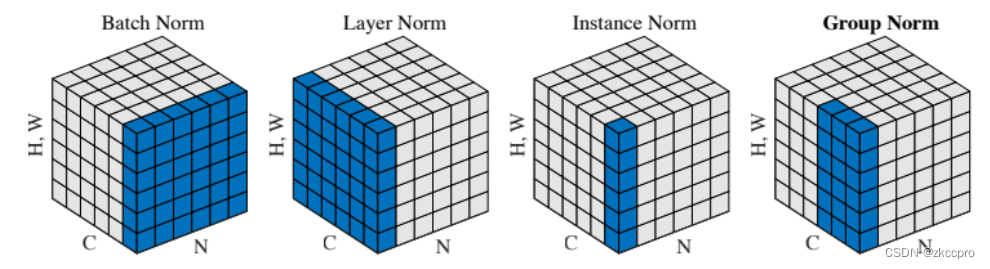
图3 4种标准化域

由(3-1)，标准化是按照标准化域计算的，标准化域就是图3中蓝色的数据。（就是对这部分数据求均值和方差）

你可以把图3中的正方体块想象成一个tensor：H、W是图像的高和宽，C是通道数，N是batch_size。也就是说，上图中的正方体块可以表示为这样的tensor(N, C, H, W)。

如此，四中标准化方法就比较好理解了：

1. Batch Norm：以batch中所有图像的一个channel为单位做标准化，标准化层参数是2C。
2. Layer Norm：以batch中一个图像的所有channel为单位做标准化，标准化层参数是2N。
3. Instance Norm：以batch中一个图像的一个channel为单位做标准化，标准化层参数是2CN。
4. Group Norm：以batch中的一个图像的group个channel为单位做标准化，标准化层参数是2NC/group。

• **tips：**对于深层网络这个东西几乎是必用的，否则到后面可能会导致模型拟合能力下降严重。而且最好是让标准化层参数加入网络梯度训练，让网络学习到一个最佳的标准化策略。

4. 权重初始化

模型要迭代训练一定要有一个初始权重，那初始权重应该取多少呢？或者说这个问题应该如何考虑呢？

我们的目标应该是这样：要使得每一层【输出o】、【输入x】、【该层反向传播时计算梯度】的【均值和方差】保持一致。

这有啥好处呢？因为如果每次迭代后输入输出分布接近一致，那么权重向量就可以在相同比例的两个空间内寻找一组最佳映射；假设每次迭代后输出的分布空间都有很大变化，则权重每次还得学习不一样的映射尺度，造成模型学习的震荡，很难收敛。

更重要的是梯度的稳定。如果每次梯度分布空间不一样，则容易造成梯度爆炸或消失的问题。

总之，我们学习一个输入和输出的映射关系，最好要排除掉变量之间分布的差异影响因素，才可以更好的学习到输入输出的本质关系。因此，初始值更要取一个

基于此目的，下面来推导一下初始权重应该取怎样的值？我们假设一个最简单的情况，一个没有非线性单元的全连接层中，输入、权重、输出三者的关系：
$$o_i=\sum _{j=1}^{n_{in}}{w}_{ij}{x}_j\text{\hspace{1em}(4-1)}$$
(4-1)中，nin为输入神经元个数。

x在输入前一般已经做了归一化处理，均值为0，方差为γ2。假设我们的ω是从某种分布中抽取的（不一定是高斯分布），该分布的均值也是0（可以证明此时输出的均值也能保证为0）方差为δ2。

那么按此计算，输出的均值和方差是多少呢？不难计算得到：
$$\begin{gathered} E(o)=0 \\ Var(o)=n_{in}{\delta }^2{\gamma }^2\text{\hspace{1em}(4-2)} \end{gathered}$$
如此，如果我们想让输入和输出的方差相等，必须令ninδ2=1。同理，在反向传播中（由该层神经元输出计算该层参数的梯度），也必须令noutδ2=1（nout为输出神经元个数）才能保证参数梯度的方差=输出的方差。据此，我们只需满足：
$${\delta }^2=\frac{2}{n_{in}+n_{out}}\text{\hspace{1em}(4-3)}$$
**我们采样 一个的(4-3)的方差，0均值的高斯分布，即可得出一层权重的初始值。这就是Xavier采样初始化。**当然，没必要非得采样高斯分布，均匀分布反而更简单计算，也很容易计算出该均匀分布的值域。