简介

在神经网络和深度学习中，激活函数（activation function）是对神经元的输出进行处理的一种函数。神经网络的激活函数必须是非线性的，它的作用是引入非线性因素，从而使神经网络可以处理更加复杂的数据，并且提高模型的准确率。

激活函数的初衷

我们使用感知机输出对应的数字0和1。但是我们发现这是一个分段函数，有两个部分组成。很是冗余，不够简便，那有没有一种可能呢，只需要一个函数就可以表示整个分段的过程，当然有，即使用激活函数。

使用激活函数h(x)来表示上述的分段函数过程，达到简化的效果。

激活函数必须是非线性函数

常见的激活函数与实现

激活函数常见的几种类型包括：

• Sigmoid函数：将输入值压缩到0和1之间，常用于二分类任务；
• tanh函数：将输入值压缩到-1和1之间，比Sigmoid函数更加对称；
• ReLU函数：常用于深度神经网络中，可以有效地避免梯度消失的问题；
• LeakyReLU函数：ReLU函数的改进版，在负数域的导数为0的情况下，引入一个小的斜率，可以缓解ReLU函数的死亡问题；
• Softmax函数：对多分类问题中的概率进行归一化，使得所有类别的概率之和为1。
• **Step跃阶函数：**简单，非线性，但由于不可导在深度学习中应用受限
  不同的激活函数在不同场景下有着不同的优缺点，需要根据具体的任务和数据进行选择。具体问题具体分析

Step跃阶函数

公式

优点

• 简单性和非线性特性

缺点

• 非导数性：Step跃阶函数不连续，不可微分，其导数在阈值处为0，这样就不利于使用梯度下降等方法优化模型参数，也不利于后向传播算法的计算。
• 饱和性：Step跃阶函数在饱和区间内输出固定值，导致了梯度消失问题，这意味着如果一个神经元在训练中被困在了饱和状态，那么它将会停止学习。

应用场景

因此，Step跃阶函数在神经网络和深度学习中的应用极其有限，通常不建议使用。实际上，为了解决其导数不连续、不可微分的问题，一些激活函数如Sigmoid、ReLU、LeakyReLU、tanh等都被提出并广泛应用。

由于其简单性和非线性特性，Step跃阶函数在一些特殊场景下仍然有一定的应用，比如在人工神经元模型中，也可以用于控制某些电路元件的开关。

代码实现

from matplotlib import pyplot as plt
import numpy as np


def step_function(x):
    y = x > 0
    print("y:",y) # 输出的布尔值
    # y = y.astype(np.int64) # 这里写int会出错
    y = [int(num) for num in y] # 与上句使用的astype效果一样
    return y

x = np.array([1.5,-2,5.0])
step_function(x)

x1 = np.arange(-6,7,1)
y1 = step_function(x1)
plt.plot(x1,y1)
plt.show()

效果图

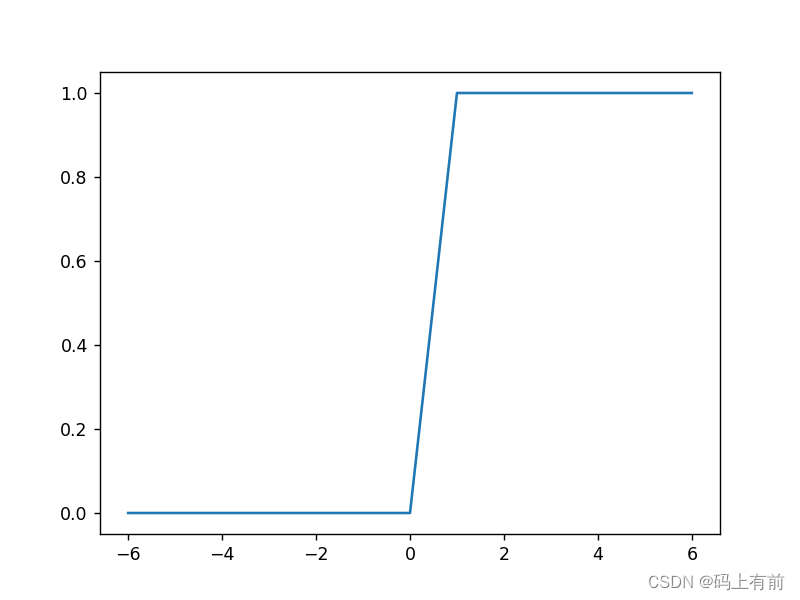
Sigmoid函数与代码实现

公式

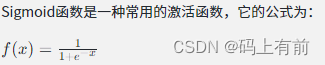
Sigmoid函数优点

• 输出值被转化到(0,1)之间，可以用来做二分类问题，表示某件事发生的概率（比如一张图片是否为猫）
• 而且它的输出值相对于输入值是可导的，可以观看函数中有e的x次方，比较好求导，非常适合用于梯度下降算法中，可以帮助神经网络更容易、更快地收敛。

Sigmoid函数缺点

• 输入很大的时候，输出函数会趋于饱和，在神经网络的后期训练中，这可能会导致梯度消失，导致网络无法学习到有效的特征。可见下图中当x的值很大或者很小时，y的值接近1和0。
• 此外，由于其非对称性，它倾向于使神经元的激活输出处于饱和状态，导致一些神经元失活，降低了神经网络的性能。

代码实现

from matplotlib import pyplot as plt
import numpy as np


def sigmoid(x):
    y = 1/(1+np.exp(-x))
    return y

x1 = np.arange(-6,7,1)
y2 = sigmoid(x1) 
plt.title("sigmoid functions") # 给图设置标题
plt.xlabel("x axis") # 设置x轴
plt.ylabel("y axis") # 设置y轴
plt.plot(x1,y2,'y') # 传入x和y的值 创建图
plt.show() # 展示图

效果图

可以发现图像处于0和1之间，因此适合进行二分类问题

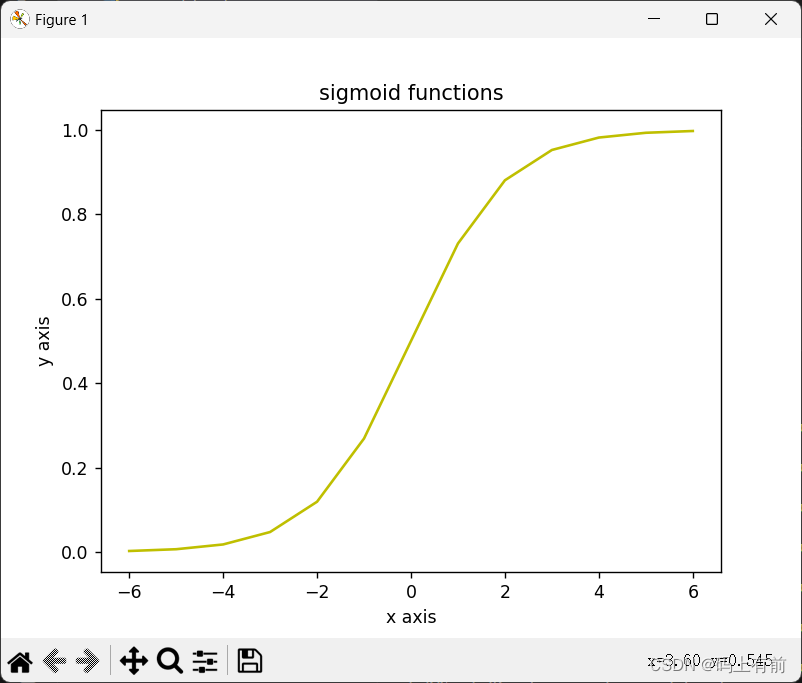
ReLu

公式

当输入x小于0时，输入y为0。当x大于等于0时，输出为x

优点

• 非线性：ReLU函数是一种非线性函数，在神经网络中可以引入非线性特征，提高模型表达能力。
• 稀疏性：ReLU函数在输入为负数时输出为0，因此可以在神经网络中产生稀疏表示，从而减少神经元的数量，提高计算效率。
• 收敛速度快：ReLU函数在输入为正数时，其导数恒为1，因此在梯度下降过程中不会出现梯度消失问题，能够加速神经网络的收敛速度。
• 计算速度快：ReLU函数简单、快速，应用更为广泛。

缺点

• 比如当输入为负数时，梯度恒为0，可能产生死亡神经元，影响模型的精度，因此需要进行一定的修正，如LeakyReLU和PReLU等。

代码

# ReLU函数相当于在自变量小于0的时候为0，
# 大于零的时候和自变量相等，也就是在自变量和0中取最大值
from matplotlib import pyplot as plt
import numpy as np


def ReLU(x):
    y = np.maximum(0,x)
    return y

x1 = np.arange(-6,7,1)
y3 = ReLU(x1)
plt.plot(x1,y3)
plt.show()

效果图

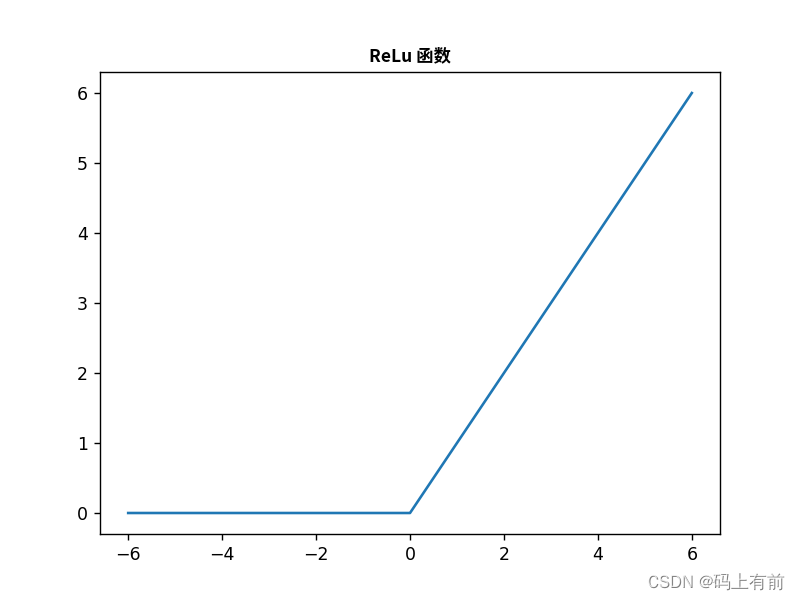
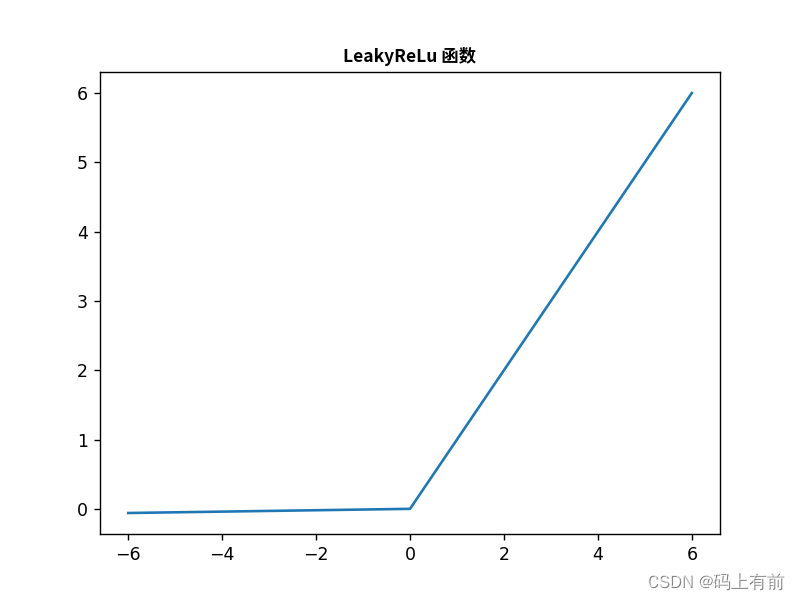
LeakyReLU

公式

其中，α是一个小于1的常数，通常取0.01。

优点

• ReLU函数的优点
• 可以缓解ReLU函数的死亡神经元问题，增强了神经网络的稳定性和泛化能力，并且在一些图像分类和对象检测等任务中取得了较好的性能表现。

缺点

• LeakyReLU函数并不能完全消除死亡神经元问题，因此可以在实际应用中使用其他方法如Dropout、Batch Normalization等进一步解决问题。

代码

from matplotlib import pyplot as plt
import matplotlib
import numpy as np

def leaky_relu(x, alpha=0.01):
    """
    LeakyReLU函数的实现
    Args:
      x: 输入向量或矩阵
      alpha: 斜率系数，一般取较小的值，默认为0.01
    Returns:
      LeakyReLU函数的输出，与输入维度相同
    """
    y = np.copy(x)
    y[y<0] *= alpha
    return y

zhfont1 = matplotlib.font_manager.FontProperties(fname="SourceHanSansSC-Bold.otf") 
plt.title("LeakyReLu 函数",fontproperties=zhfont1)

x1 = np.arange(-6,7,1,dtype=np.float64)
y3 = leaky_relu(x1)
plt.plot(x1,y3)
plt.show()

效果图

tanh

公式

优点

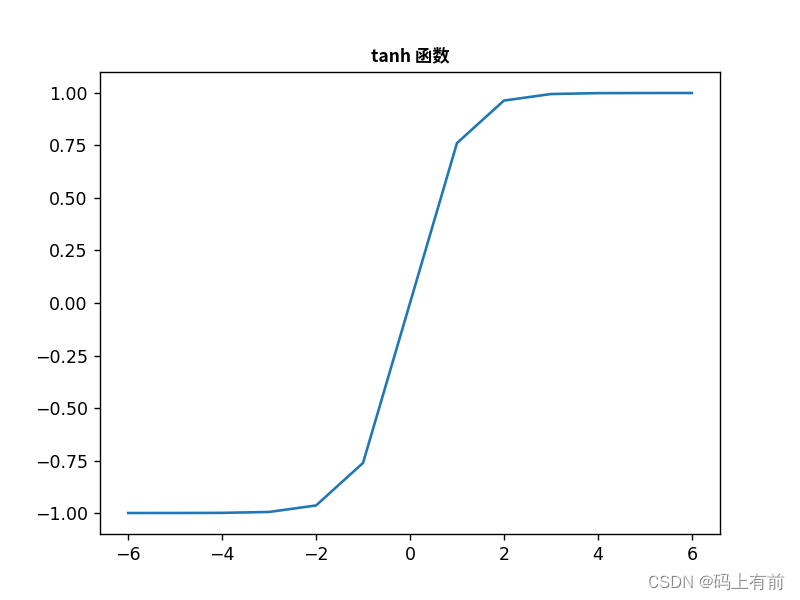
• tanh函数同样可以将输入值映射到一个**[-1, 1]的区间内**，而且在输入值接近0时，tanh函数的输出值变化范围更大，具有更强的非线性特征。

缺点

• 需要注意的是，与Sigmoid函数一样，tanh函数也存在梯度消失的问题，这可能导致模型训练困难，因此在一些深层神经网络的应用中，需要采用其他类型的激活函数和优化策略来解决问题。

应用场景

tanh函数在神经网络中常用于处理具有正负值的数据，比如图像、音频等数据。同时，tanh函数在神经网络中也是一种常用的激活函数，主要应用于RNN网络中的LSTM、GRU等模型，能够平衡模型的记忆能力和遗忘能力，提高模型的性能和鲁棒性。

代码

import matplotlib
from matplotlib import pyplot as plt
import numpy as np

def tanh(x):
    """
    双曲正切函数的实现
    Args:
      x: 输入向量或矩阵
    Returns:
      tanh函数的输出，与输入维度相同
    """
    return np.tanh(x)

zhfont1 = matplotlib.font_manager.FontProperties(fname="SourceHanSansSC-Bold.otf") 
plt.title("tanh 函数",fontproperties=zhfont1)

x1 = np.arange(-6,7,1,dtype=np.float64)
y3 = tanh(x1)
plt.plot(x1,y3)
plt.show()

效果图

Softmax

公式

Softmax函数将输入向量中的每个元素从实数范围映射到(0,1)之间，且使输出向量中所有元素之和为1，因此输出向量可被理解为一个概率分布，其中每个元素表示对应类别的预测概率。在神经网络中，通常将Softmax函数作为最后一层的激活函数来输出分类预测结果。

代码

import matplotlib
from matplotlib import pyplot as plt
import numpy as np

def softmax(x, axis=-1):
    """
    Softmax函数的实现
    Args:
      x: 输入向量或矩阵
      axis: 指定沿哪个维度进行Softmax操作，默认为最后一个维度
    Returns:
      Softmax函数的输出，与输入维度相同
    """
    # 将输入减去最大值，避免指数爆炸
    x_exp = np.exp(x - np.max(x, axis=axis, keepdims=True))
    # 计算Softmax分母
    x_sum = np.sum(x_exp, axis=axis, keepdims=True)
    # 计算Softmax输出
    return x_exp / x_sum

zhfont1 = matplotlib.font_manager.FontProperties(fname="SourceHanSansSC-Bold.otf") 
plt.title("softmax 函数",fontproperties=zhfont1)

x1 = np.arange(-6,7,1,dtype=np.float64)
y3 = softmax(x1)
plt.plot(x1,y3)
plt.show()

效果图