前言
前面介绍了队列,栈等线性数据结构,二叉树,AVL树等非线性数据结构,本节,我们介绍一种新的非线性数据结构:图。图这种结构有很广泛的应用,比如社交网络,电子地图,多对多的关系都可以用图来表示。
1. 概念
图(Graph),是一种复杂的非线性表结构。
图中的元素我们就叫做顶点(vertex)
图中的一个顶点可以与任意其他顶点建立连接关系。我们把这种建立的关系叫做边(edge)
跟顶点相连接的边的条数叫做度(degree)
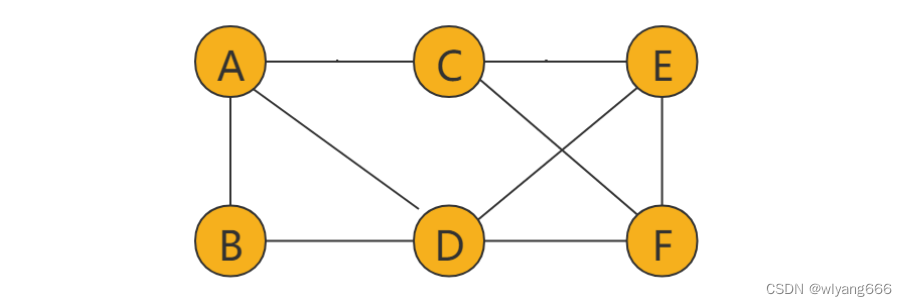
图这种结构有很广泛的应用,比如社交网络,电子地图,多对多的关系就可以用图来表示。
边有方向的图叫做有向图,比如A点到B点的直线距离,微信的添加好友是双向的
边无方向的图叫无向图,比如网络拓扑图
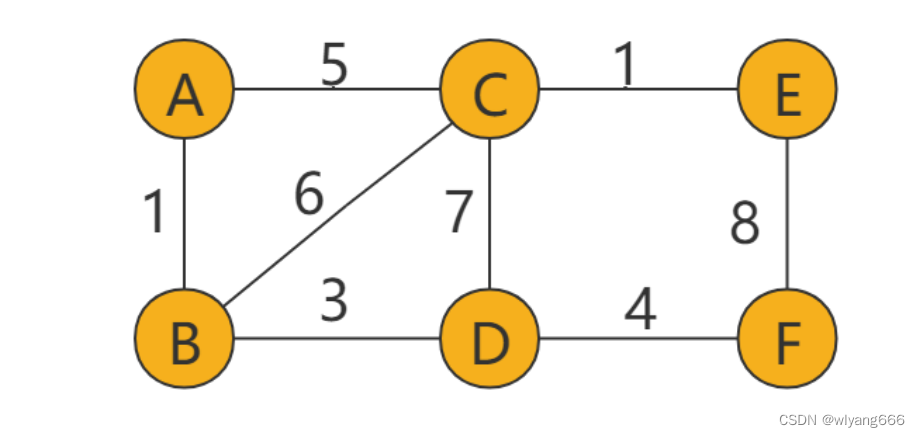
带权图(weighted graph)。在带权图中,每条边都有一个权重(weight),我们可以通过这个权重来表示 一些可度量的值
2. 存储
2.1 邻接矩阵
2.1.1 原理介绍
图最直观的一种存储方法就是,邻接矩阵(Adjacency Matrix)。邻接矩阵的底层是一个二维数组
无向图:如果顶点 i 与顶点 j 之间有边,我们就将 A[i][j]和 A[j][i]标记为 1
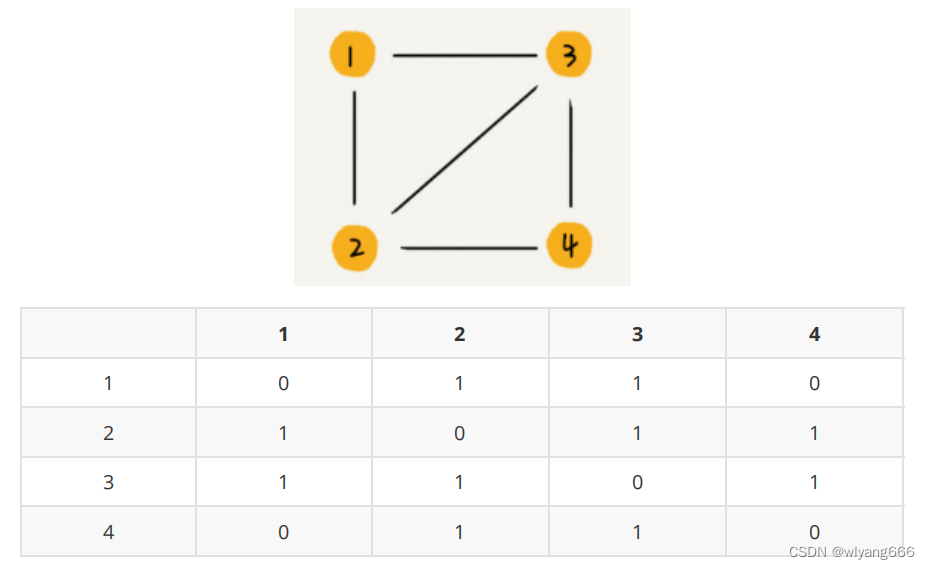
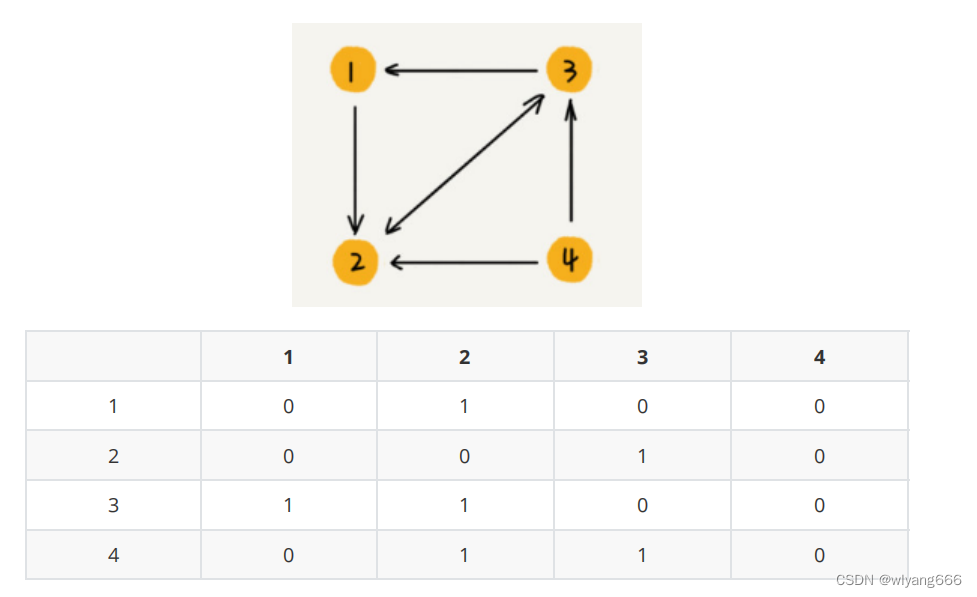
有向图:
如果顶点 i 到顶点 j 之间,有一条箭头从顶点 i 指向顶点 j 的边,那我们就将 A[i][j]标记为 1。同理,如果有一条箭头从顶点 j 指向顶点 i 的边,我们就将 A[j][i]标记为 1
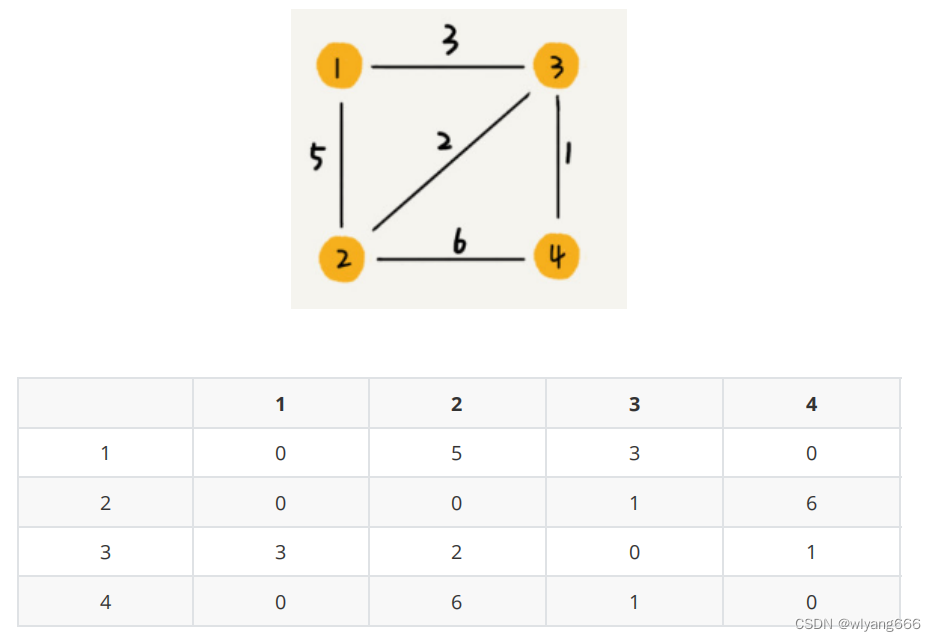
带权图:
数组中就存储相应的权重
2.1.2 代码实现
package org.wanlong.graph;
import java.util.ArrayList;
import java.util.List;
/**
* @author wanlong
* @version 1.0
* @description: 邻接矩阵实现图
* @date 2023/6/16 11:09
*/
public class AdjacencyMatrix {
private List vertexList;//存储点的链表
private int[][] edges;//邻接矩阵,用来存储边
private int numOfEdges;//边的数目
public AdjacencyMatrix(int n) {
//初始化矩阵,一维数组,和边的数目
edges = new int[n][n];
vertexList = new ArrayList(n);
numOfEdges = 0;
}
//得到结点的个数
public int getNumOfVertex() {
return vertexList.size();
}
//得到边的数目
public int getNumOfEdges() {
return numOfEdges;
}
//返回结点i的数据
public Object getValueByIndex(int i) {
return vertexList.get(i);
}
//返回v1,v2的权值
public int getWeight(int v1, int v2) {
return edges[v1][v2];
}
//插入结点
public void insertVertex(Object vertex) {
vertexList.add(vertex);
}
//插入边
public void insertEdge(int v1, int v2, int weight) {
edges[v1][v2] = weight;
numOfEdges++;
}
public static void main(String args[]) {
int n = 4, e = 4;//分别代表结点个数和边的数目
String labels[] = {"V1", "V1", "V3", "V4"};//结点的标识
AdjacencyMatrix graph = new AdjacencyMatrix(n);
for (String label : labels) {
graph.insertVertex(label);//插入结点
}
//插入四条边
graph.insertEdge(0, 1, 2);
graph.insertEdge(0, 2, 5);
graph.insertEdge(2, 3, 8);
graph.insertEdge(3, 0, 7);
System.out.println("结点个数是:" + graph.getNumOfVertex());
System.out.println("边的个数是:" + graph.getNumOfEdges());
}
}
2.2 邻接表
2.2.1 原理介绍
用邻接矩阵来表示一个图,虽然简单、直观,但是比较浪费存储空间。
对于无向图来说,如果 A[i][j]等于 1,那 A[j][i]也肯定等于 1。实际上,我们只需要存储一个就可以了。也就是说,无向图的二维数组中,如果我们将其用对角线划分为上下两部分,那我们只需要利用上面或者下面这样一半的空间就足够了,另外一半白白浪费掉了。
还有,如果我们存储的是稀疏图(Sparse Matrix),也就是说,顶点很多,但每个顶点的边并不多,那邻接矩阵的存储方法就更加浪费空间了。比如微信有好几亿的用户,对应到图上就是好几亿的顶点。但是每个用户的好友并不会很多,一般也就三五百个而已。如果我们用邻接矩阵来存储,那绝大部分的存储空间都被浪费了。
针对上面邻接矩阵比较浪费内存空间的问题,我们来看另外一种图的存储方法,邻接表(AdjacencyList)
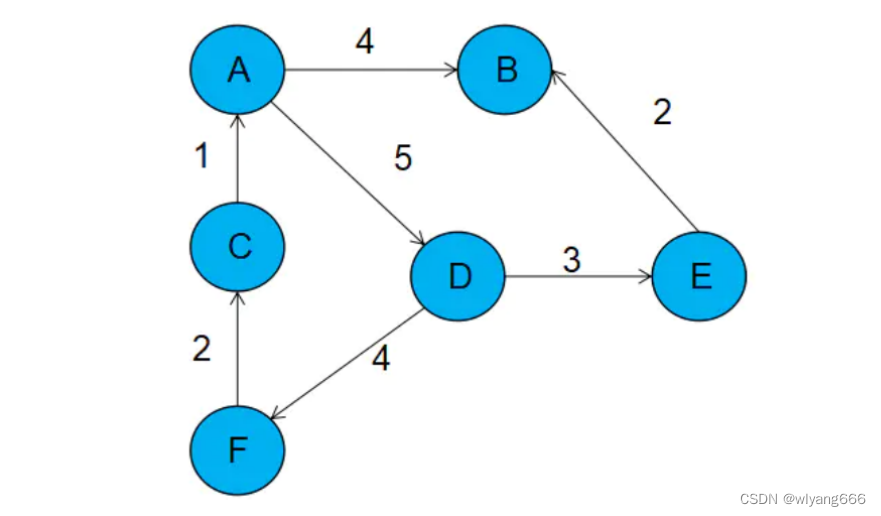
每个顶点对应一条链表,链表中存储的是与这个顶点相连接的其他顶点。图中画的是一个有向图的邻接表存储方式,每个顶点对应的链表里面,存储的是指向的顶点。前面的数组存储的是所有的顶点,每一个顶点后面连接的块代表前面顶点所指向的顶点和路线的权值。如果该点还指向其他顶点,则继续在块后面添加。例如A指向了B权值是4,那么A后面就加上一块,之后发现A还指向D权值是5,那么就在块尾继续添加一块。其实也就是数组+链表的结构。
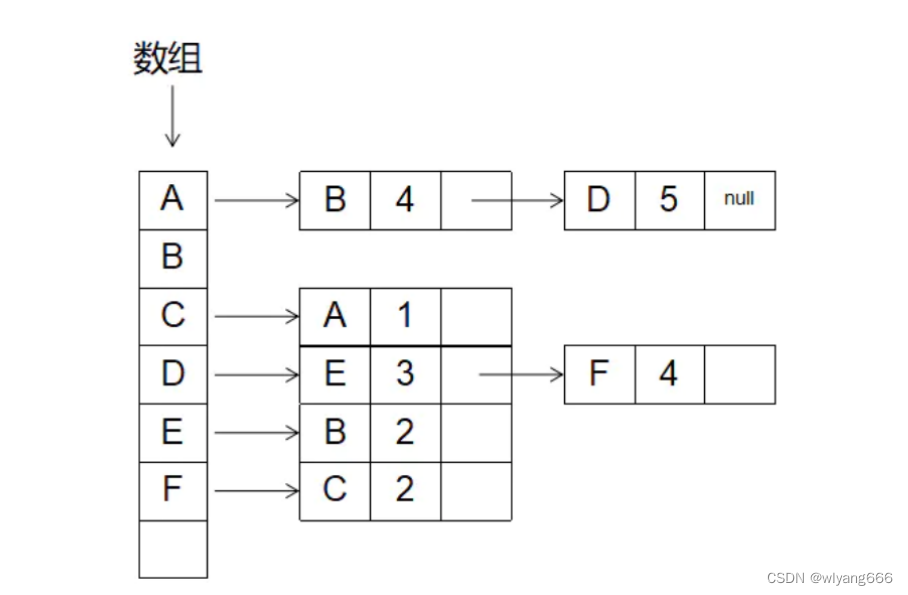
根据邻接表的结构和图,我们不难发现,图其实是由顶点和边组成的。所以我们就抽象出两种类,一个是Vertex顶点类,一个是Edge边类
2.2.2 代码实现
2.2.2.1 定义顶点类
package org.wanlong.graph;
/**
* @author wanlong
* @version 1.0
* @description: 顶点
* @date 2023/6/16 11:13
*/
public class Vertex {
String name; //顶点名称
Edge next; //从该定点出发的边
public Vertex(String name, Edge next){
this.name = name;
this.next = next;
}
}
2.2.2.2 定义边类
package org.wanlong.graph;
/**
* @author wanlong
* @version 1.0
* @description: 边
* @date 2023/6/16 11:13
*/
public class Edge {
String name; //被指向的顶点
int weight; //弧的权值
Edge next; //被指向的下一个边
public Edge(String name, int weight, Edge next){
this.name = name;
this.weight = weight;
this.next = next;
}
}
2.2.2.3 定义邻接表类
package org.wanlong.graph;
import java.util.HashMap;
import java.util.Iterator;
import java.util.Map;
import java.util.Set;
/**
* @author wanlong
* @version 1.0
* @description: 邻接表
* @date 2023/6/16 11:15
*/
public class AdjacencyList {
Map<String, Vertex> vertexsMap; //存储所有的顶点
AdjacencyList() {
this.vertexsMap = new HashMap<>();
}
public void insertVertex(String vertexName) { //添加顶点
Vertex vertex = new Vertex(vertexName, null);
vertexsMap.put(vertexName, vertex);
}
public void insertEdge(String begin, String end, int weight) {
//添加弧
Vertex beginVertex = vertexsMap.get(begin);
if (beginVertex == null) {
beginVertex = new Vertex(begin, null);
vertexsMap.put(begin, beginVertex);
}
Edge edge = new Edge(end, weight, null);
if (beginVertex.next == null) {
beginVertex.next = edge;
} else {
Edge lastEdge = beginVertex.next;
while (lastEdge.next != null) {
lastEdge = lastEdge.next;
}
lastEdge.next = edge;
}
}
public void print() { //打印图
Set<Map.Entry<String, Vertex>> set = vertexsMap.entrySet();
Iterator<Map.Entry<String, Vertex>> iterator = set.iterator();
while (iterator.hasNext()) {
Map.Entry<String, Vertex> entry = iterator.next();
Vertex vertex = entry.getValue();
Edge edge = vertex.next;
while (edge != null) {
System.out.println(vertex.name + " 指向 " + edge.name + " 权值 为:" + edge.weight);
edge = edge.next;
}
}
}
public static void main(String[] args) {
AdjacencyList graph = new AdjacencyList();
graph.insertVertex("A");
graph.insertVertex("B");
graph.insertVertex("C");
graph.insertVertex("D");
graph.insertVertex("E");
graph.insertVertex("F");
graph.insertEdge("C", "A", 1);
graph.insertEdge("F", "C", 2);
graph.insertEdge("A", "B", 4);
graph.insertEdge("E", "B", 2);
graph.insertEdge("A", "D", 5);
graph.insertEdge("D", "F", 4);
graph.insertEdge("D", "E", 3);
graph.print();
}
}
3. 遍历
遍历是指从某个节点出发,按照一定的的搜索路线,依次访问对数据结构中的全部节点,且每个节点仅访问一次
前面已经讲过了二叉树的节点遍历。类似的,图的遍历是指,从给定图中任意指定的顶点(称为初始点)出发,按照某种搜索方法沿着图的边访问图中的所有顶点,使每个顶点仅被访问一次,这个过程称为图的遍历。遍历过程中得到的顶点序列称为图遍历序列。
3.1 深度优先遍历(DFS)
深度优先搜索,从起点出发,从规定的方向中选择其中一个不断地向前走,直到无法继续为止,然后尝试另外一种方向,直到最后走到终点。就像走迷宫一样,尽量往深处走。
DFS 解决的是连通性的问题,即,给定两个点,一个是起始点,一个是终点,判断是不是有一条路径能从起点连接到终点。起点和终点,也可以指的是某种起始状态和最终的状态。问题的要求并不在乎路径是长还是短,只在乎有还是没有。
3.1.1 深度遍历过程
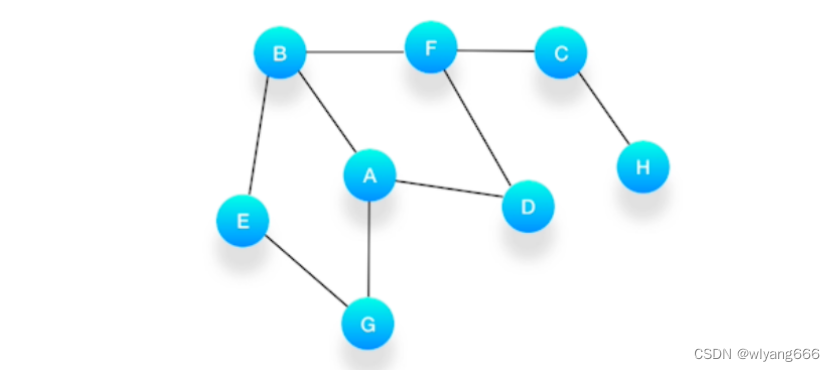
假设我们有这么一个图,里面有A、B、C、D、E、F、G、H 8 个顶点,点和点之间的联系如下图所示,对这个图进行深度优先的遍历。
必须依赖栈(Stack),特点是后进先出(LIFO)。
-
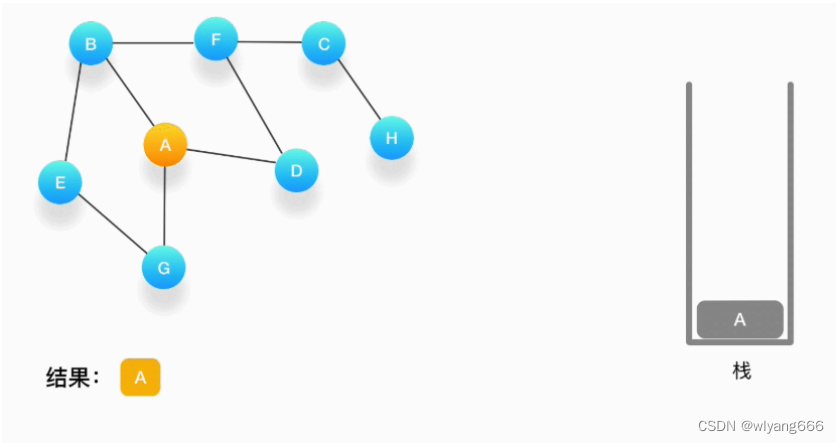
选择一个起始顶点,例如从顶点 A 开始。把 A 压入栈,标记它为访问过(用红色标记),并输出到结果中
-
寻找与 A 相连并且还没有被访问过的顶点,顶点 A 与 B、D、G 相连,而且它们都还没有被访问过,我们按照字母顺序处理,所以将 B 压入栈,标记它为访问过,并输出到结果中。
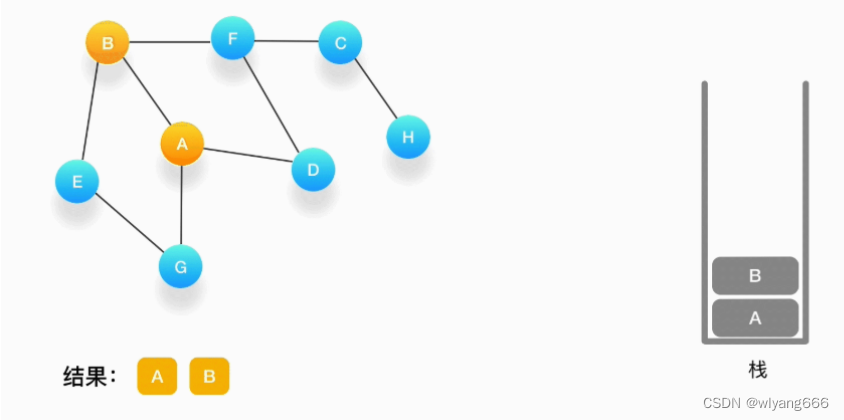
-
现在我们在顶点 B 上,重复上面的操作,由于 B 与 A、E、F 相连,如果按照字母顺序处理的话,A 应该是要被访问的,但是 A 已经被访问了,所以我们访问顶点 E,将 E 压入栈,标记它为访问过,并输出到结果中。
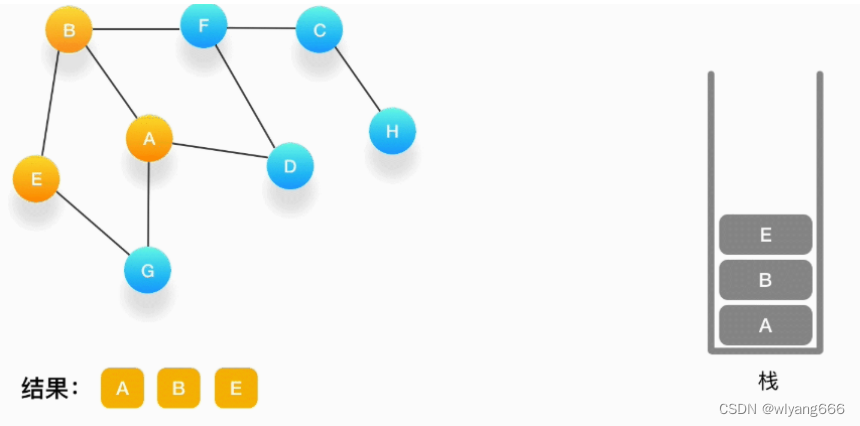
-
从 E 开始,E 与 B、G 相连,但是B刚刚被访问过了,所以下一个被访问的将是G,把G压入栈,标记它为访问过,并输出到结果中。
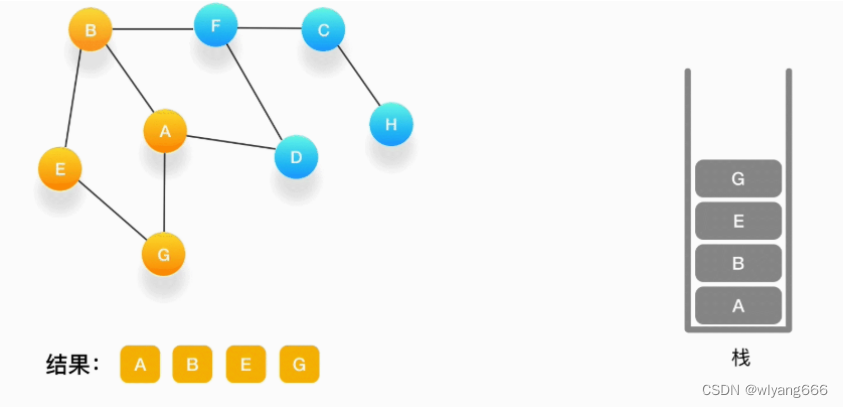
-
现在我们在顶点 G 的位置,由于与 G 相连的顶点都被访问过了,类似于我们走到了一个死胡同,必须尝试其他的路口了。所以我们这里要做的就是简单地将 G 从栈里弹出,表示我们从 G 这里已经无法继续走下去了,看看能不能从前一个路口找到出路。
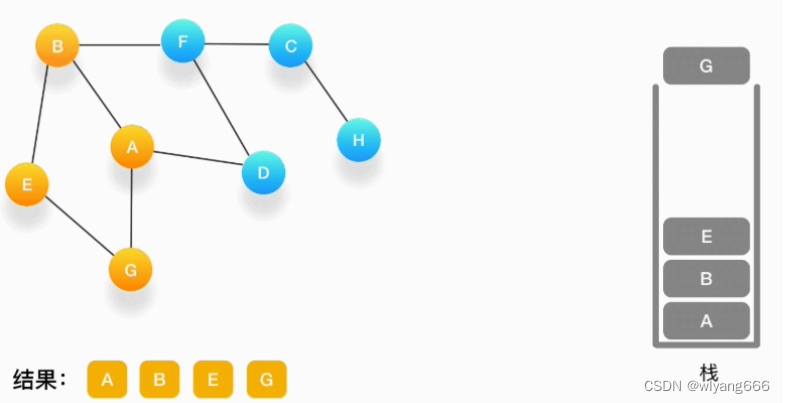
-
如果发现周围的顶点都被访问了,就把当前的顶点弹出。现在栈的顶部记录的是顶点 E,我们来看看与 E 相连的顶点中有没有还没被访问到的,发现它们都被访问了,所以把 E 也弹出去。
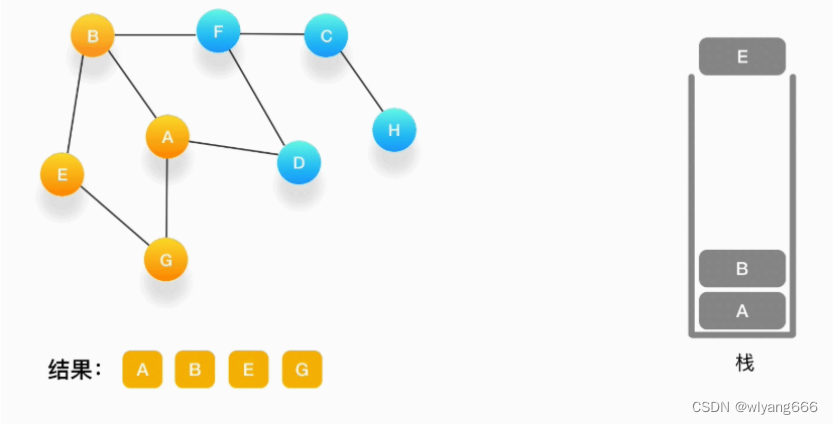
-
当前栈的顶点是 B,看看它周围有没有还没被访问的顶点,有,是顶点 F,于是把 F 压入栈,标记它为访问过,并输出到结果中。
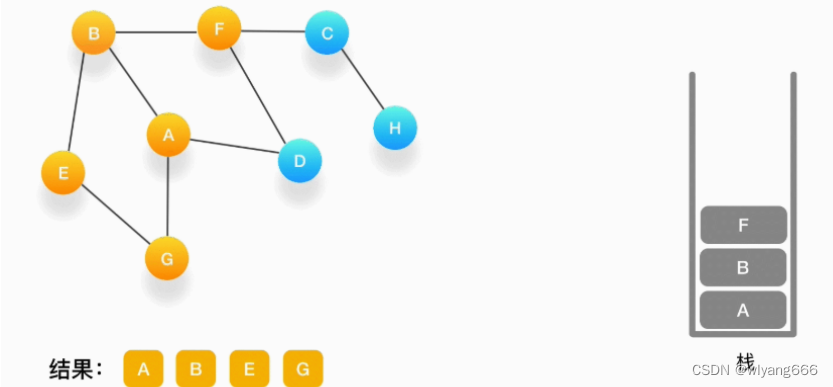
-
当前顶点是 F,与 F 相连并且还未被访问到的点是 C 和 D,按照字母顺序来,下一个被访问的点是 C,将 C 压入栈,标记为访问过,输出到结果中。
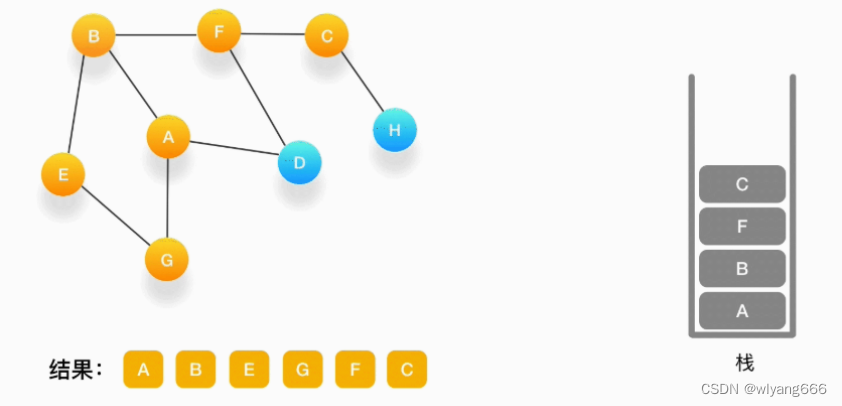
-
当前顶点为 C,与 C 相连并尚未被访问到的顶点是 H,将 H 压入栈,标记为访问过,输出到结果中。
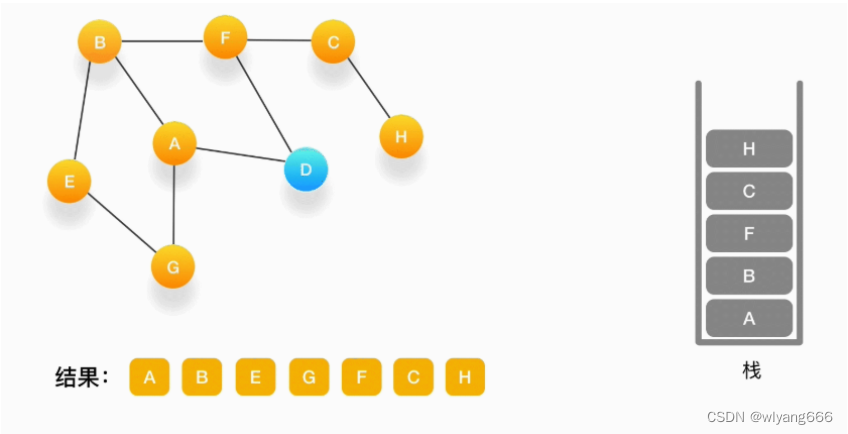
-
当前顶点是 H,由于和它相连的点都被访问过了,将它弹出栈。
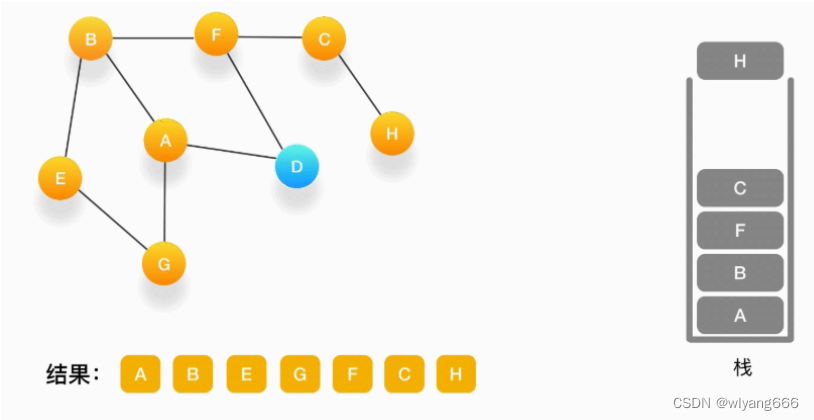
-
当前顶点是 C,与 C 相连的点都被访问过了,将 C 弹出栈。
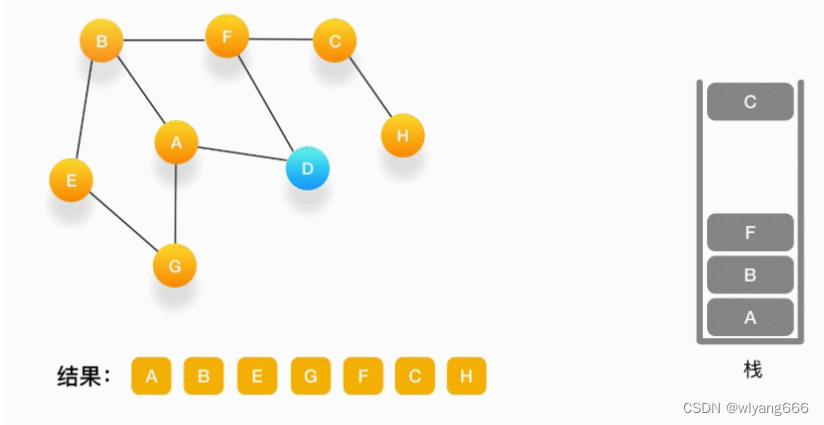
-
当前顶点是 F,与 F 相连的并且尚未访问的点是 D,将 D 压入栈,输出到结果中,并标记为访问过。
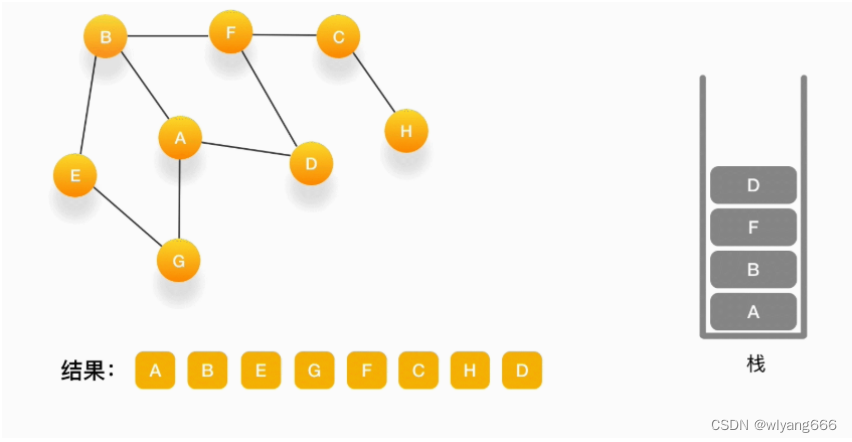
-
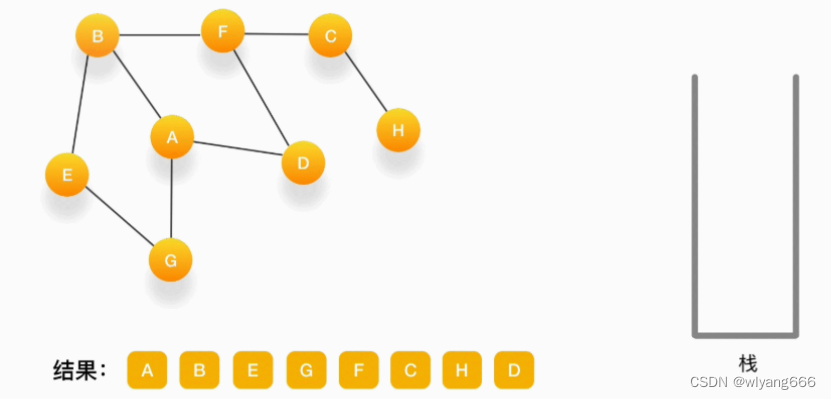
当前顶点是 D,与它相连的点都被访问过了,将它弹出栈。以此类推,顶点 F,B,A 的邻居都被访问过了,将它们依次弹出栈就好了。最后,当栈里已经没有顶点需要处理了,我们的整个遍历结束
3.1.2 时间复杂度
邻接表:
访问所有顶点的时间为 O(V,而查找所有顶点的邻居一共需要 O(E) 的时间,所以总的时间复杂度是O(V + E)。
邻接矩阵:
查找每个顶点的邻居需要 O(V) 的时间,所以查找整个矩阵的时候需要 O(V2)的时间
3.2 广度优先遍历
直观地讲,它其实就是一种“地毯式”层层推进的搜索策略,即先查找离起始顶点最近的,然后是次近的,依次往外搜索。
3.2.1 广度优先遍历过程
假设我们有这么一个图,里面有A、B、C、D、E、F、G、H 8 个顶点,点和点之间的联系如下图所示,对这个图进行广度优先的遍历。
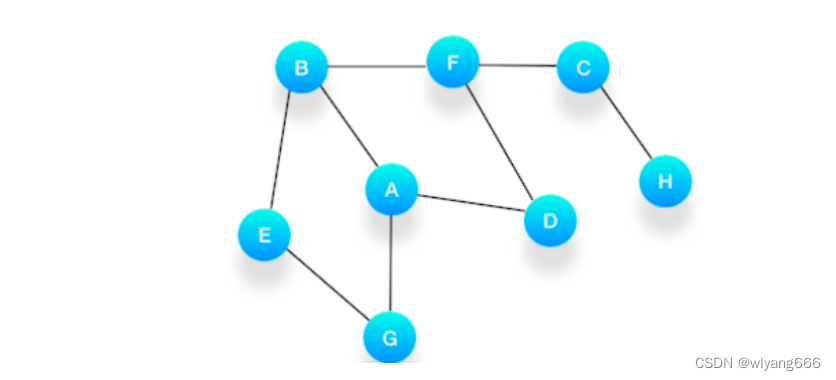
**依赖队列(Queue),先进先出(FIFO)。**一层一层地把与某个点相连的点放入队列中,处理节点的时候正好按照它们进入队列的顺序进行。
- 选择一个起始顶点,让我们从顶点 A 开始。把 A 压入队列,标记它为访问过(用黄色标记)。
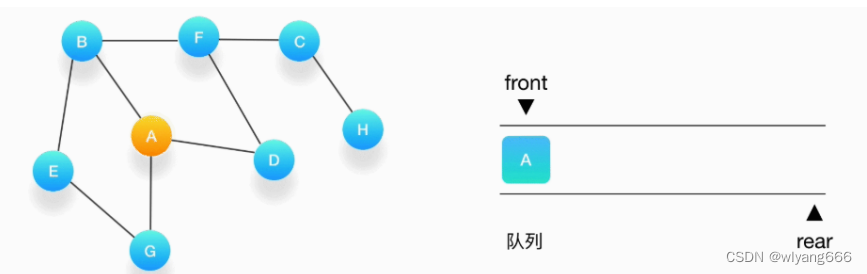
- 从队列的头取出顶点 A,打印输出到结果中,同时将与它相连的尚未被访问过的点按照字母大小顺序压入队列,同时把它们都标记为访问过,防止它们被重复地添加到队列中。
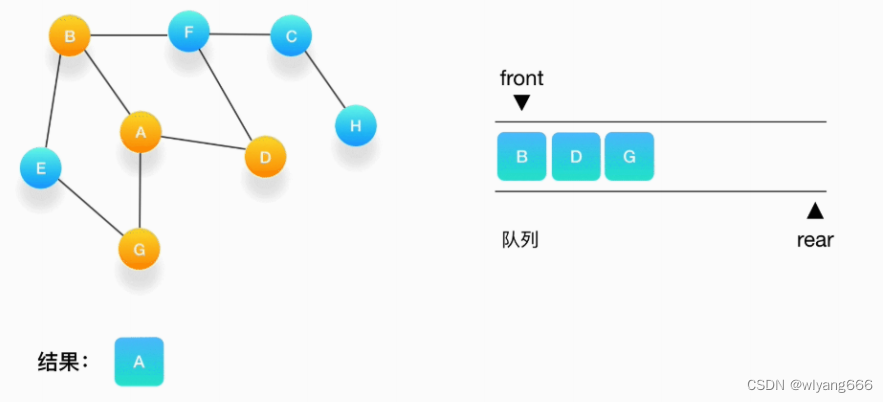
- 从队列的头取出顶点 B,打印输出它,同时将与它相连的尚未被访问过的点(也就是 E 和 F)压入队列,同时把它们都标记为访问过。
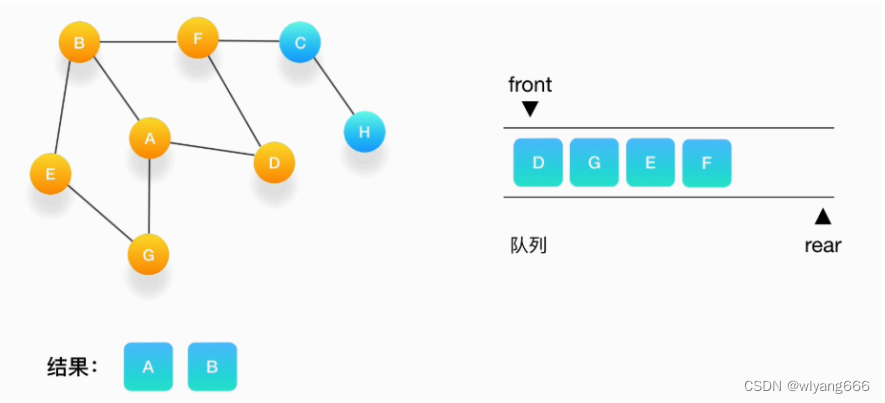
- 继续从队列的头取出顶点 D,打印输出它,此时我们发现,与 D 相连的顶点 A 和 F 都被标记访问过了,所以就不要把它们压入队列里。
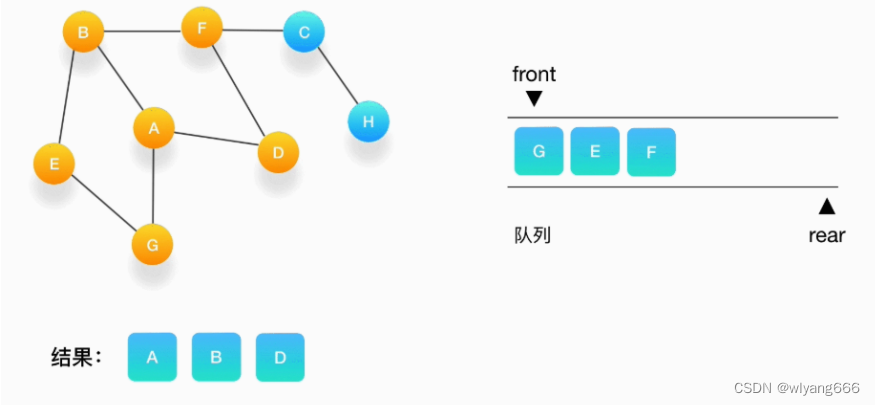
- 接下来,队列的头是顶点 G,打印输出它,同样的,G 周围的点都被标记访问过了。我们不做任何处理。
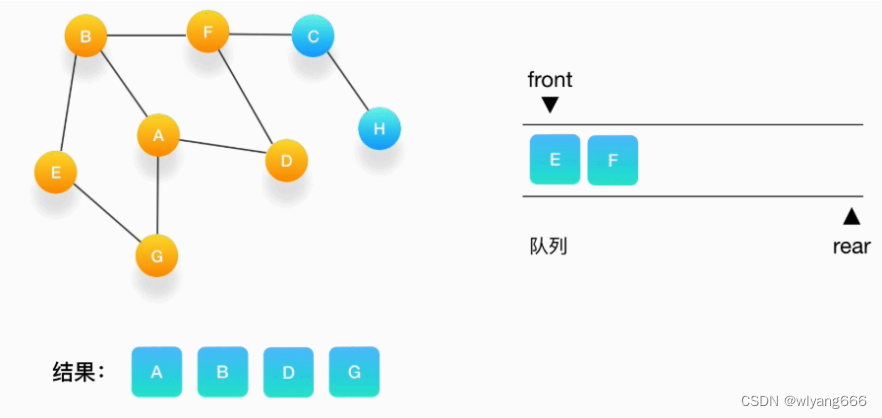
- 队列的头是 E,打印输出它,它周围的点也都被标记为访问过了,我们不做任何处理。
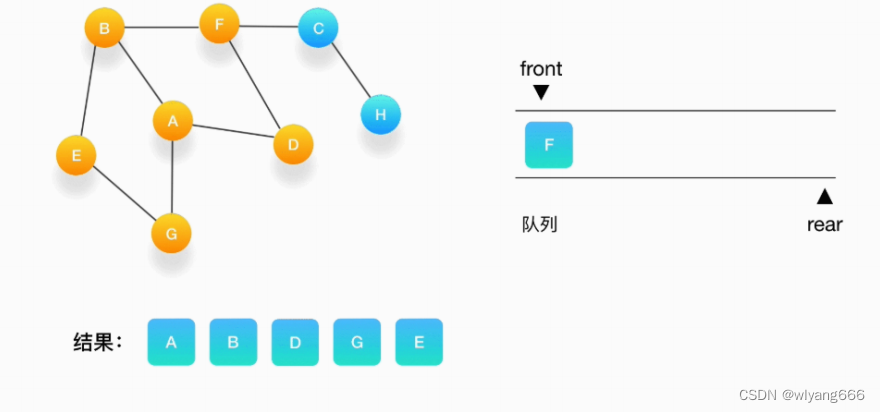
- 接下来轮到顶点 F,打印输出它,将 C 压入队列,并标记 C 为访问过。
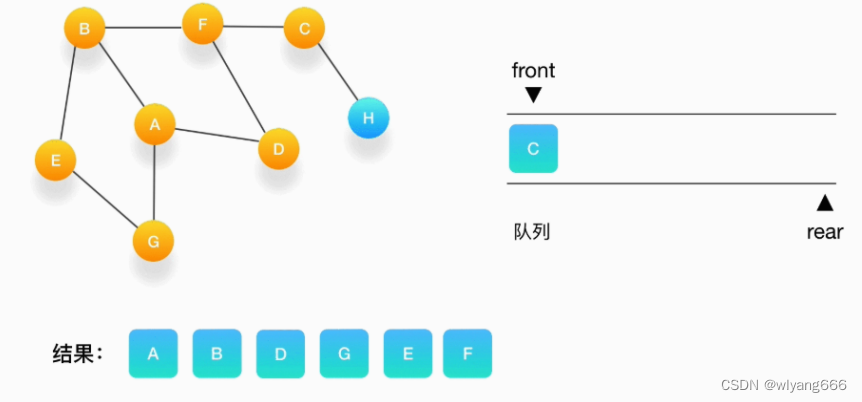
- 将 C 从队列中移出,打印输出它,与它相连的 H 还没被访问到,将 H 压入队列,将它标记为访问过。
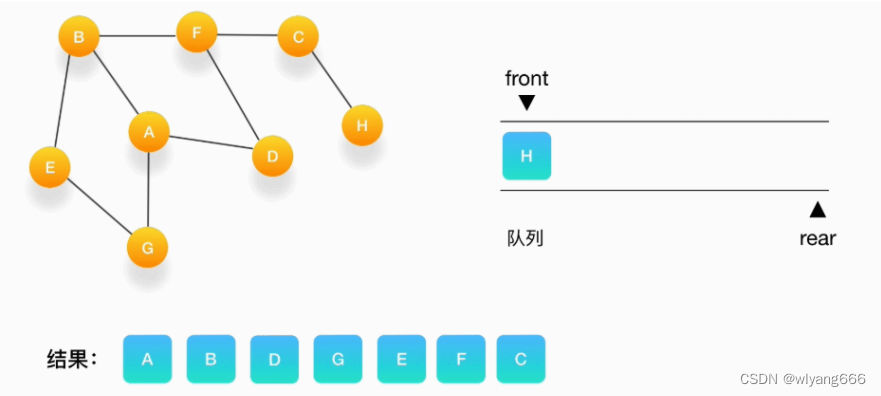
- 队列里只剩下 H 了,将它移出,打印输出它,发现它的邻居都被访问过了,不做任何事情。
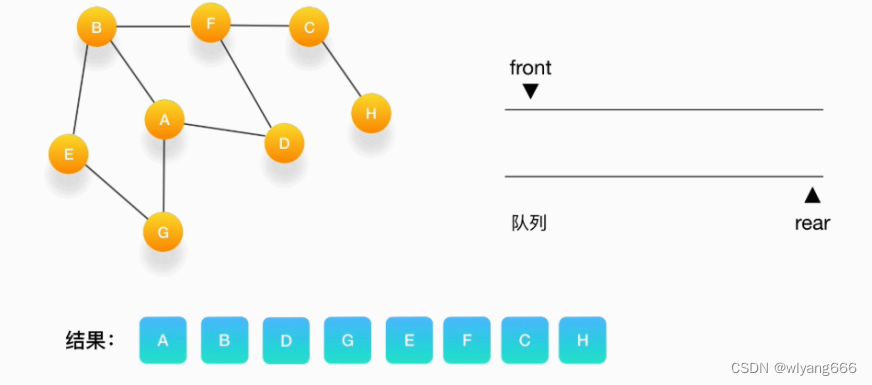
- 队列为空,表示所有的点都被处理完毕了,程序结束。
3.2.2 时间复杂度
邻接表:
每个顶点都需要被访问一次,时间复杂度是 OV);相连的顶点(也就是每条边) 也都要被访问一次,加起来就是 O(E)。因此整体时间复杂度就是 O(V+E)。
邻接矩阵:
V个顶点,每次都要检查每个顶点与其他顶点是否有联系,因此时间复杂度是 O(V^2)。
3.2.3 应用
广度优先的搜索可以同时从起始点和终点开始进行,称之为双端 BFS。这种算法往往可以大大地提高搜索的效率。社交网络可以用图来表示。这个问题就非常适合用图的广度优先搜索算法来解决,因为广度优先搜索是层层往外推进的。首先,遍历与起始顶点最近的一层顶点,也就是用户的一度好友,然后再遍历与用户距离的边数为 2 的顶点,也就是二度好友关系,以及与用户距离的边数为 3 的顶点,也就是三度好友关系。