🔥 本文由 程序喵正在路上 原创,CSDN首发!
💖 系列专栏:数据结构与算法
🌠 首发时间:2022年12月6日
🦋 欢迎关注🖱点赞👍收藏🌟留言🐾
🌟 一以贯之的努力 不得懈怠的人生
阅读指南
- B树
- B树的插入
- B树的删除
- B+树
- B树 VS B+树
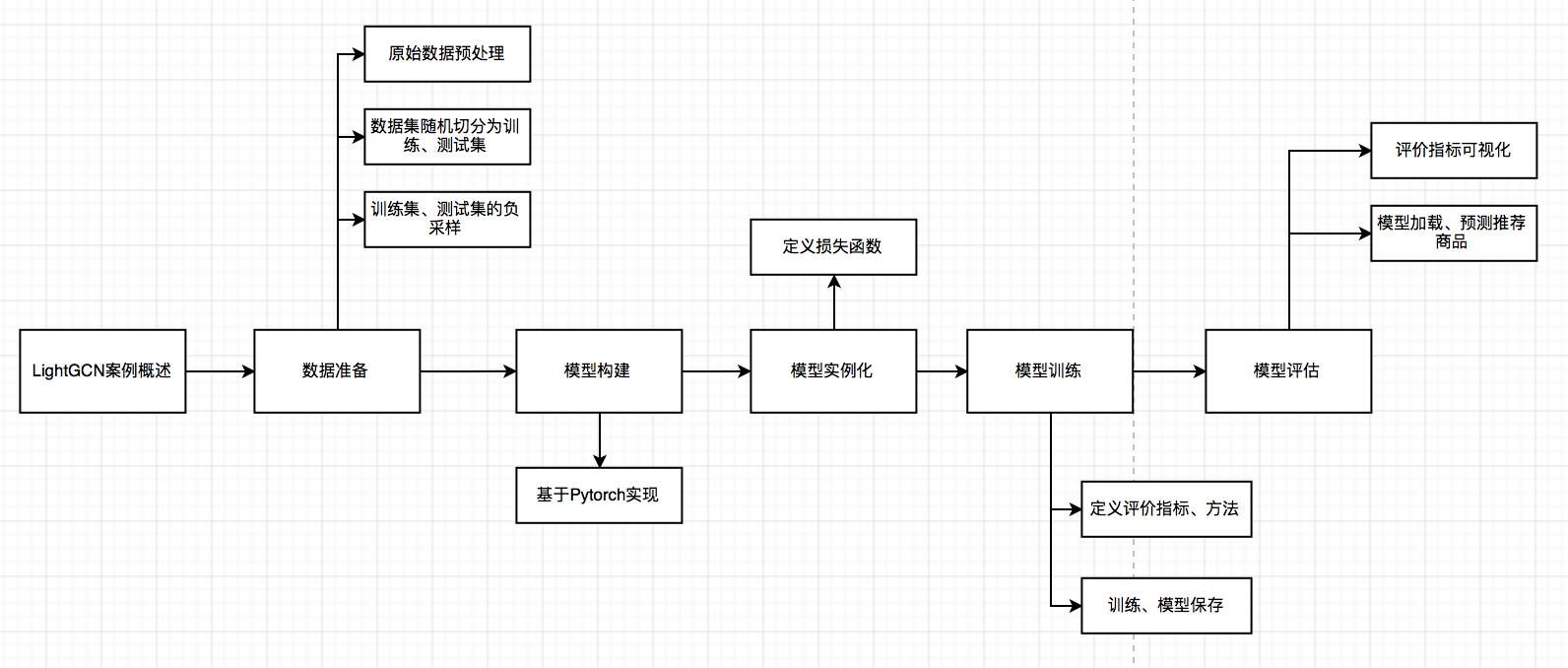
B树
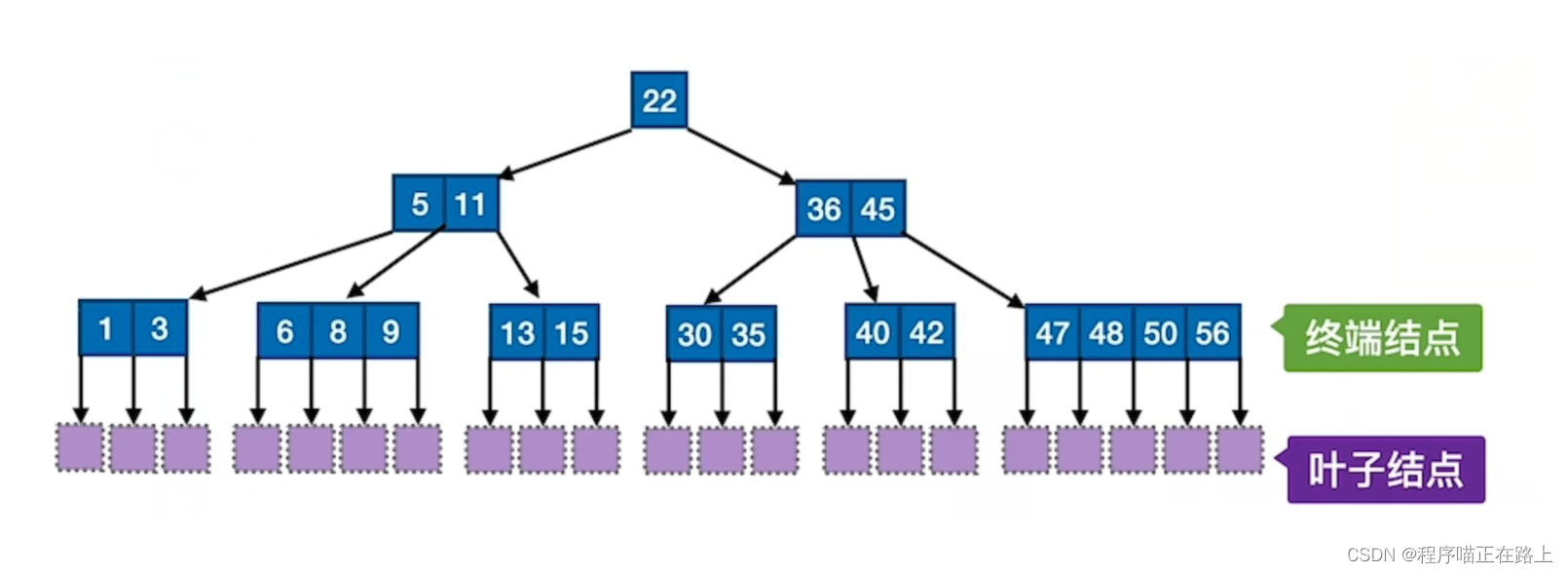
B B B 树,又称为多路平衡查找树, B B B 树中所有结点的孩子个数的最大值称为 B B B 树的阶,通常用 m m m 表示,上图即为 5 5 5 阶 B B B 树。一棵 m m m 阶 B B B 树或为空树,或为满足如下特性的 m m m 叉树:
-
树中每个结点至多有 m m m 棵子树,即至多含有 m − 1 m - 1 m−1 个关键字
-
若根结点不是终端结点,则至少有两棵子树
-
除根结点外的所有非叶结点至少有 ⌈ m / 2 ⌉ \lceil m/2 \rceil ⌈m/2⌉ 棵子树,即至少含有 ⌈ m / 2 ⌉ − 1 \lceil m/2 \rceil - 1 ⌈m/2⌉−1 个关键字
-
所有的叶结点都出现在同一层次上,并且不带信息(可以视为外部结点或类似于折半查找判定树的查找失败结点,实际上这些结点并不存在,指向这些结点的指针为空)
-
所有非叶结点的结构如下:

其中, K i ( i = 1 , 2 , . . . , n ) K_i \ (i = 1, 2, ..., n) Ki (i=1,2,...,n) 为结点的关键字,且满足 K 1 < K 2 < . . . < K n K_1 < K_2 < ... < K_n K1<K2<...<Kn; P i ( i = 0 , 1 , . . . , n ) P_i \ (i = 0, 1, ..., n) Pi (i=0,1,...,n) 为指向子树根结点的指针,且指针 P i − 1 P_{i-1} Pi−1 所指子树中所有结点的关键字均小于 K i K_i Ki, P i P_{i} Pi 所指子树中所有结点的关键字均大于 K i K_i Ki, n ( ⌈ m / 2 ⌉ − 1 ≤ n ≤ m − 1 ) n \ (\lceil m/2 \rceil - 1 \leq n \leq m - 1) n (⌈m/2⌉−1≤n≤m−1) 为结点中关键字的个数
m m m 阶 B B B 树的核心特性:
- 根结点的子树数 ∈ [ 2 , m ] \in [2, m] ∈[2,m],关键字数 ∈ [ 1 , m − 1 ] \in [1, m - 1] ∈[1,m−1];其他结点的子树数 ∈ [ ⌈ m / 2 ⌉ , m ] \in [\lceil m/2 \rceil, m] ∈[⌈m/2⌉,m],关键字数 ∈ [ ⌈ m / 2 ⌉ − 1 , m − 1 ] \in [\lceil m/2 \rceil -1, m - 1] ∈[⌈m/2⌉−1,m−1]
- 对于任一结点,其所有子树的高度都相同
- 关键字的值:子树 0 < 0 < 0< 关键字 1 < 1 < 1< 子树 1 < 1 < 1< 关键字 2 < 2 < 2< 子树 2 < 2 < 2< . . . ... ... (类比二叉查找树 左 < < < 中 < < < 右)
问:含 n n n 个关键字的 m m m 阶 B B B 数,最小高度和最大高度是多少?
最小高度 —— 让每个结点尽可能地满,每个结点都有 m − 1 m-1 m−1 个关键字, m m m 个分叉,则可以得到公式 n ≤ ( m − 1 ) ( 1 + m + m 2 + m 3 + . . . + m h − 1 = m h − 1 n \leq (m - 1)(1 + m + m^2 + m^3 + ... + m^{h - 1} = m^h - 1 n≤(m−1)(1+m+m2+m3+...+mh−1=mh−1,因此 h ≥ l o g m ( n + 1 ) h \geq log_m(n + 1) h≥logm(n+1)
最大高度 —— 让各层的分叉尽可能地少,即根结点只有 2 2 2 个分叉,其他结点只有 ⌈ m / 2 ⌉ \lceil m/2 \rceil ⌈m/2⌉ 个分叉,各层结点至少有:第一层 1 1 1、第二层 2 2 2、第三层 2 ⌈ m / 2 ⌉ . . . 2 \lceil m/2 \rceil ... 2⌈m/2⌉... 第 h h h 层 2 ( ⌈ m / 2 ⌉ ) h − 2 2 (\lceil m/2 \rceil)^{h - 2} 2(⌈m/2⌉)h−2,第 h + 1 h + 1 h+1 层共有叶子结点(失败结点) 2 ( ⌈ m / 2 ⌉ ) h − 1 2 (\lceil m/2 \rceil)^{h - 1} 2(⌈m/2⌉)h−1
n n n 个关键字的 B B B 树必有 n + 1 n + 1 n+1 个叶子结点,则 n + 1 ≥ 2 ( ⌈ m / 2 ⌉ ) h − 1 n + 1 \geq 2 (\lceil m/2 \rceil)^{h - 1} n+1≥2(⌈m/2⌉)h−1,即 h ≤ l o g ⌈ m / 2 ⌉ n + 1 2 + 1 h \leq log_{\lceil m/2 \rceil} \frac{n + 1}{2} + 1 h≤log⌈m/2⌉2n+1+1
我们可以用表格的形式更直观地来计算最大高度:
记 k = ⌈ m / 2 ⌉ k = \lceil m/2 \rceil k=⌈m/2⌉
| 层数 | 最少结点数 | 最少关键字数 |
|---|---|---|
| 第一层 | 1 1 1 | 1 1 1 |
| 第二层 | 2 2 2 | 2 ( k − 1 ) 2(k - 1) 2(k−1) |
| 第三层 | 2 k 2k 2k | 2 k ( k − 1 ) 2k(k - 1) 2k(k−1) |
| 第四层 | 2 k 2 2k^2 2k2 | 2 k 2 ( k − 1 ) 2k^2(k - 1) 2k2(k−1) |
| … | … | … |
| 第 h h h 层 | 2 k h − 2 2k^{h-2} 2kh−2 | 2 k h − 2 ( k − 1 ) 2k^{h-2}(k - 1) 2kh−2(k−1) |
从表格中我们可以得到: h h h 层的 m m m 阶 B B B 树至少包含关键字总数 1 + 2 ( k − 1 ) ( k 0 + k 1 + k 2 + . . . + k h − 2 = 1 + 2 ( k h − 1 − 1 ) 1 + 2(k -1)(k^0 + k^1 + k^2 + ... + k^{h - 2} = 1 + 2(k^{h - 1} - 1) 1+2(k−1)(k0+k1+k2+...+kh−2=1+2(kh−1−1)
若关键字总数少于这个值,则高度一定小于 h h h,因此 n ≥ 1 + 2 ( k h − 1 − 1 ) n \geq 1 + 2(k^{h - 1} - 1) n≥1+2(kh−1−1),得: h ≤ l o g k n + 1 2 + 1 = l o g ⌈ m / 2 ⌉ n + 1 2 + 1 h \leq log_{k} \frac{n + 1}{2} + 1 = log_{\lceil m/2 \rceil} \frac{n + 1}{2} + 1 h≤logk2n+1+1=log⌈m/2⌉2n+1+1
所以含 n n n 个关键字的 m m m 阶 B B B 数, l o g m ( n + 1 ) ≤ h ≤ l o g ⌈ m / 2 ⌉ n + 1 2 + 1 log_m(n + 1) \leq h \leq log_{\lceil m/2 \rceil} \frac{n + 1}{2} + 1 logm(n+1)≤h≤log⌈m/2⌉2n+1+1
B树的插入
核心要求:
- 对于 m m m 阶 B B B 树 —— 除根结点外,结点关键字个数 ⌈ m / 2 ⌉ − 1 ≤ n ≤ m − 1 \lceil m/2 \rceil - 1 \leq n \leq m- 1 ⌈m/2⌉−1≤n≤m−1
- 子树 0 < 0 < 0< 关键字 1 < 1 < 1< 子树 1 < 1 < 1< 关键字 2 < 2 < 2< 子树 2 < 2 < 2< . . . ... ...
构建 B B B 树时,如果在插入新的关键字后,导致原结点的关键字数超过上限,则从中间位置( ⌈ m / 2 ⌉ \lceil m/2 \rceil ⌈m/2⌉)将其中的关键字分为两部分,左部分包含的关键字放在原结点中,右部分包含的关键字放到新结点中,中间位置( ⌈ m / 2 ⌉ \lceil m/2 \rceil ⌈m/2⌉)的结点插入原结点的父结点;若此时导致其父结点的关键字个数也超过了上限,则继续进行这种分裂操作,直至这个过程传到根结点为止,进而导致 B B B 树高度增 1 1 1
每次插入新元素一定是插入到最底层 “终端结点”,用 “查找” 来确定插入位置
B树的删除
① 若被删除的关键字在终端结点,则直接删除该关键字即可(注意结点关键字个数是否低于下限 ⌈ m / 2 ⌉ − 1 \lceil m/2 \rceil - 1 ⌈m/2⌉−1
② 若被删除的关键字在非终端结点,则用直接前驱或直接后继来替代被删除的关键字
- 直接前驱:当前关键字左侧指针所指子树中 “最右下” 的元素
- 直接后继:当前关键字右侧指针所指子树中 “最左下” 的元素
所以对非终端结点关键字的删除必然可以转化为对终端结点的删除操作
③ 兄弟够借。若被删除的关键字所在结点删除前的关键字个数低于下限,且与此结点右(或左)兄弟结点的关键字个数还很宽裕,则需要调整该结点、右(或左)兄弟结点及其双亲结点(父子换位法)
④ 兄弟不够借。若被删除的关键字所在结点删除前的关键字个数低于下限,且此时与该结点相邻的左、右兄弟结点的关键字个数均 = ⌈ m / 2 ⌉ − 1 = \lceil m/2 \rceil - 1 =⌈m/2⌉−1,则将关键字删除后与左(或右)兄弟结点及双亲结点中的关键字进行合并
在合并过程中,双亲结点中的关键字个数会减 1 1 1。若其双亲结点是根结点且关键字个数减少至 0 0 0(根结点关键字个数为 1 1 1 时,有 2 2 2 棵子树),则直接将根结点删除,合并后的新结点成为根;若双亲结点不是根结点,且关键字个数减少到 ⌈ m / 2 ⌉ − 2 \lceil m/2 \rceil - 2 ⌈m/2⌉−2,则又要与它自己的兄弟结点进行调整或合并操作,并重复上述操作,直至符合 B B B 树的要求为止
B+树
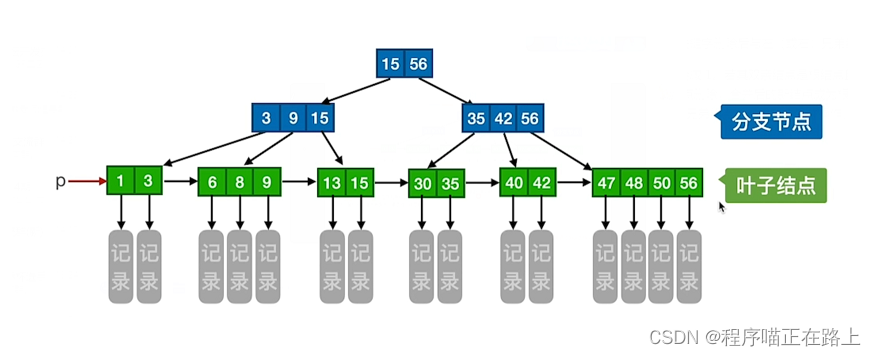
上图是一棵 4 4 4 阶 B + B+ B+ 树
一棵 m m m 阶 B + B+ B+ 树需满足下列条件:
- 每个分支结点最多有 m m m 棵子树(孩子结点)
- 非叶根结点至少有两颗子树,其他每个分支结点至少有 ⌈ m / 2 ⌉ \lceil m/2 \rceil ⌈m/2⌉ 棵子树
- 结点的子树个数与关键字个数相等
- 所有叶结点包含全部关键字及指向相应记录的指针,叶结点中将关键字按大小顺序排序,并且相邻叶结点按大小顺序相互连接起来
- 所有分支结点中仅包含它的各个子结点中关键字的最大值及指向其子结点的指针
B树 VS B+树
m m m 阶 B B B 树:
- 结点中的 n n n 个关键字对应 n + 1 n + 1 n+1 棵子树
- 根结点的关键字数 n ∈ [ 1 , m − 1 ] n \in [1, m-1] n∈[1,m−1],其他结点的关键字数 n ∈ [ ⌈ m / 2 ⌉ − 1 , m − 1 ] n \in [\lceil m/2 \rceil - 1, m - 1] n∈[⌈m/2⌉−1,m−1]
- 在 B B B 树中,各结点中包含的关键字是不重复的
- B B B 树的结点中都包含了关键字对应的记录的存储地址
m m m 阶 B + B+ B+ 树:
- 结点中的 n n n 个关键字对应 n n n 棵子树
- 根结点的关键字数 n ∈ [ 1 , m ] n \in [1, m] n∈[1,m],其他结点的关键字数 n ∈ [ ⌈ m / 2 ⌉ , m ] n \in [\lceil m/2 \rceil, m] n∈[⌈m/2⌉,m]
- 在 B + B+ B+ 树中,叶结点包含全部关键字,非叶结点中出现过的关键字也会出现在叶结点中
- 在 B + B+ B+ 树中,叶结点包含信息,所有非叶结点仅起索引作用,非叶结点中的每个索引项只含有对应子树的最大关键字和指向该子树的指针,不含有该关键字对应记录的存储地址




![[附源码]Python计算机毕业设计Django四川景区管理系统](https://img-blog.csdnimg.cn/272ac698d5274cc48367960d1466a506.png)



![[C语言数据结构]树](https://img-blog.csdnimg.cn/f55c5f179d784a4cadc99e33d1c0ce1d.png#pic_center)