引言

这是统计学习方法第十一章条件随机场的阅读笔记，包含所有公式的详细推导。

条件随机场(conditional random field,CRF)是给定一组输入随机变量条件下另一组输出随机变量的条件概率分布模型，其特点是假设输出随机变量构成马尔可夫随机场。

建议先阅读概率图简介，了解一些概率图的知识。

---

1. 《统计学习方法》——条件随机场(上)
2. 《统计学习方法》——条件随机场(中)
3. 《统计学习方法》——条件随机场(下)
4. 《统计学习方法》——条件随机场#习题解答#

---

习题解答

习题11.1

  写出图11.3中无向图描述的概率图模型的因子分解式。

图11.3 无向图的团和最大团

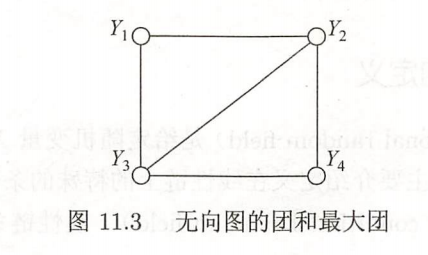
根据因子分解式的定义：将概率无向图模型的联合概率分布表示为其最大团上的随机变量的函数的乘积形式的操作，称为概率无向图模型的因子分解。

上图中包括两个最大团： { Y 1 , Y 2 , Y 3 } \{Y_1,Y_2,Y_3\} {Y1​,Y2​,Y3​}和 { Y 2 , Y 3 , Y 4 } \{Y_2,Y_3,Y_4\} {Y2​,Y3​,Y4​}。

可以得因子分解：
$$P(Y)=\frac{{\Psi }_{(1,2,3)}(Y_{(1,2,3)})\cdot {\Psi }_{(2,3,4)}(Y_{(2,3,4)})}{{\sum }_y[{\Psi }_{(1,2,3)}(Y_{(1,2,3)})\cdot {\Psi }_{(2,3,4)}(Y_{(2,3,4)})]}$$

习题11.2

  证明$Z(x)=a_n^T(x)\cdot 1=1^T\cdot {\beta }_0(x)$，其中$1$是元素均为1的$m$维列向量。

在前文的前向后向算法推导中有证明。

习题11.3

  写出条件随机场模型学习的梯度下降法。

条件随机场可表示为

$$\begin{gathered} P(y|x)=\frac{1}{Z(x)}\exp \sum _{k=1}^K{w}_k{f}_k(y,x) \\ Z(x)=\sum _y\exp \sum _{k=1}^K{w}_k{f}_k(y,x) \end{gathered}$$

当$P_w$是一个由式$(11.15)$和式$(11.16)$给出的条件随机场模型时，对数似然函数为
$$L(w)=\sum _{j=1}^N\sum _{k=1}^K{w}_k{f}_k(y_j,x_j)-\sum _{j=1}^N\log Z_w(x_j)$$
将目标函数转换成$f(w)=-L(w)$，即通过极小化$f(w)$来更新$w$。

目标函数的梯度为：
$$g(w)=\nabla f(w^{(k)})=\left(\frac{\partial f(w)}{\partial w_1},\frac{\partial f(w)}{\partial w_2},\cdots ,\frac{\partial f(w)}{\partial w_k}\right)$$
其中每项

$$\begin{array}{rl}\frac{\partial f(w)}{\partial w_i}& =-\sum _{j=1}^N{f}_i(y_j,x_j)+\sum _{j=1}^N\frac{1}{Z_w(x_j)}\cdot \frac{\partial Z_w(x_j)}{\partial w_i}\\ & =-\sum _{j=1}^N{f}_i(y_j,x_j)+\sum _{j=1}^N\frac{1}{Z_w(x_j)}\cdot \sum _y\left[\left(\exp \sum _{k=1}^K{w}_k{f}_k(y,x_j)\right)\cdot f_k(y,x_j)\right]\end{array}$$

得到梯度下降法算法如下：

输入： 目标函数$f(w)$，梯度函数$g(w)=\nabla f(w)$，计算精度$ϵ$；

输出： $f(w)$的极小点$w^{\ast }$。

(1) 取初值$w^{(0)}\in {\mathbb{R}}^n$，令$k=0$。

(2) 计算$f(w^{(k)})$。

(3) 计算梯度$g_k=g(w^{(k)})$，当$||g_k||<ϵ$时，停止迭代，令$w^{\ast }=w^{(k)}$；否则，令$p_k=-g(w^{(k)})$，求${\lambda }_k$使
$$f(w^{(k)}+{\lambda }_k{p}_k)=\underset{\lambda \ge 0}{\min }f(w^{(k)}+\lambda p_k)$$
(4) 置$w^{(k+1)}=w^{(k)}+{\lambda }_k{p}_k$，计算$f(w^{(k+1)})$

当$||f(w^{(k+1)})-f(w^{(k)})||<ϵ$或$||w^{(k+1)}-w^{(k)}||<ϵ$时，停止迭代，令$w^{\ast }=w^{(k+1)}$。

(5) 否则，置$k=k+1$，转(3)。

习题11.4

参考图11.6的状态路径图，假设随机矩阵$M_1(x),M_2(x),M_3(x),M_4(x)$分别是
$$\begin{gathered} M_1(x)=\left[\begin{array}{cc}0& 0\\ 0.5& 0.5\end{array}\right],M_2(x)=\left[\begin{array}{cc}0.3& 0.7\\ 0.7& 0.3\end{array}\right] \\ {M}_3(x)=\left[\begin{array}{cc}0.5& 0.5\\ 0.6& 0.4\end{array}\right],M_4(x)=\left[\begin{array}{cc}0& 1\\ 0& 1\end{array}\right] \end{gathered}$$
求以$\text{start}=2$为起点$\text{stop}=2$为终点的所有路径的状态序列$y$的概率及概率最大的状态序列。

这里简单地通过代码实现一下，下一篇文章会基于Pytorch实现一个可以自动求导的CRF模型，然后用于LSTM和BERT等模型上来解决NER等问题。

from itertools import product

class CRF:
  def __init__(self, matrices, start, stop):
    self.matrices = matrices
    self.start = start
    self.stop = stop
    self.path_prob = []

  def _generate_path(self):
    """生成所有可能的路径"""
    step_num = len(self.matrices) - 1
    options = [1, 2] # 可能的状态
    middle_states = list(product(options, repeat=step_num))
    paths = [[self.start] + list(path) + [self.stop] for path in middle_states ]

    return paths

  def compute(self):
    """计算所有可能路径对应的非规范化概率，并按照概率排序"""
    paths = self._generate_path()
    for path in paths:
      prob = 1
      for i in range(len(path)-1):
        from_ = path[i]
        to = path[i+1]
        prob *= self.matrices[i][from_-1][to-1] # 基于公式11.24
      
      self.path_prob.append((prob, path))
    
    self.path_prob.sort(key=lambda x: x[0], reverse=True)
    self.show()
  
  def show(self):
    idx = 0
    for prob, path in self.path_prob:
      print(f"Path: {'→'.join([str(x) for x in path])}  Probility: {prob:.3f} {'☆' if idx ==0 else ''}")
      idx += 1

    
    

输出：

Path: 2→1→2→1→2  Probility: 0.210 ☆
Path: 2→2→1→1→2  Probility: 0.175 
Path: 2→2→1→2→2  Probility: 0.175 
Path: 2→1→2→2→2  Probility: 0.140 
Path: 2→2→2→1→2  Probility: 0.090 
Path: 2→1→1→1→2  Probility: 0.075 
Path: 2→1→1→2→2  Probility: 0.075 
Path: 2→2→2→2→2  Probility: 0.060