1.题目

题目描述

        In 1742, Christian Goldbach, a German amateur mathematician, sent a letter to Leonhard Euler in which he made the following conjecture: 
Every even number greater than 4 can be written as the sum of two odd prime numbers.
        For example: 
                8 = 3 + 5. Both 3 and 5 are odd prime numbers. 
                20 = 3 + 17 = 7 + 13. 
                42 = 5 + 37 = 11 + 31 = 13 + 29 = 19 + 23.
        Today it is still unproven whether the conjecture is right. (Oh wait, I have the proof of course, but it is too long to write it on the margin of this page.) 
        Anyway, your task is now to verify Goldbach's conjecture for all even numbers less than a million. 

输入

        the input will contain one or more test cases. 
        Each test case consists of one even integer n with 6 <= n < 1000000. 
        Input will be terminated by a value of 0 for n.

输出

        For each test case, print one line of the form n = a + b, where a and b are odd primes. Numbers and operators should be separated by exactly one blank like in the sample output below. If there is more than one pair of odd primes adding up to n, choose the pair where the difference b - a is maximized. If there is no such pair, print a line saying "Goldbach's conjecture is wrong."

样例输入

8
20
42
0

样例输出

8 = 3 +5
20 = 3 +17
42 = 5 +37

2.中文翻译

题目描述

        1742年，德国业余数学家克里斯蒂安·戈德巴赫写信给莱昂哈德·欧拉，他在信中做出了以下猜想：每个大于4的偶数都可以写成两个奇数素数的和。

        例如：

        8＝3+5。3和5都是奇数素数

        20=3+17=7+13

        42=5+37=11+31=13+29=19+23。

        今天，这个猜想是否正确还未得到证实。（哦，等等，我当然有证据，但太长了，不能写在这页的页边空白处。）

        不管怎样，你现在的任务是验证所有小于一百万的偶数的哥德巴赫猜想。

输入

        输入将包含一个或多个测试用例

        每个测试用例由一个偶数整数n组成，其中6<=n<100000

        输入将由n的值0终止。

输出

        对于每个测试用例，打印一行形式为n=a+b，其中a和b是奇素数。数字和运算符应该像下面的示例输出中那样用一个空格分隔。如果有一对以上的奇数素数加起来为n，则选择差值b-a最大的一对。如果没有这样的配对，则输出： "Goldbach's conjecture is wrong."

样例输入

8
20
42
0

样例输出

8 = 3 +5
20 = 3 +17
42 = 5 +37

3.思路解析

        1.首先必须搞清楚欧拉筛的作用和代码实现 ：视频讲解

        （这很重要！！！搞不懂就别看下面的了省的浪费时间）

        怎样才算搞懂了，就是你心里可以自己算出下面张表的时候（n=29）：

                  

 

        2.素数打表：把小于n的素数找出来并保存在列表primes中（利用欧拉筛）

        3.然后遍历primes从小到大

        4.遍历的原则是，判断i 和 n-i是否都在这个表中 。

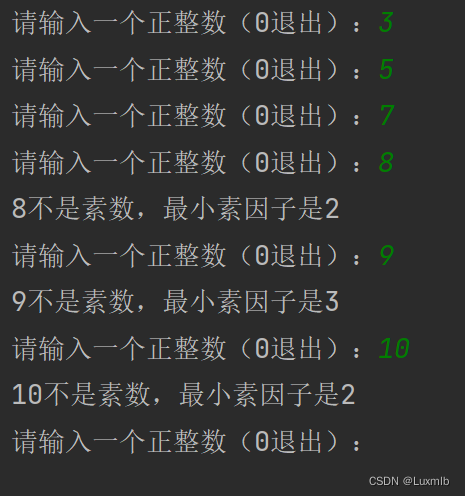
        5.下面的代码是利用一个欧拉筛判断n是否是素数输出最小素数因子的程序：思路讲解

def euler_sieve(): #欧拉筛
    for i in range(2,m+1):
        if status[i]:
            if n % i == 0:
                return i
            primes.append(i)
        for pj in primes:
            if pj * i >m:
                break
            status[pj*i]= False
            if i % pj == 0:
                break
    return False

while True:
    n =int(input("请输入一个正整数（0退出）："))
    m=int(sqrt(n))
    primes= []
    status= [False]*2 + [True] *(m-1)
    pr= euler_sieve()
    if pr:
        print("{}不是素数，最小素因子是{}".format(n,pr))

                如果是素数 就不输出 返回 True 如果不是素数就返回False :

                                       

 4.欧拉筛的作用

        1.提高代码效率

        2. 快速地找出小于或等于给定上限的所有素数，并且可以在较短的时间内计算

            出大量素数。使用欧拉筛，我们可以通过逐步排除合数的方式来确定素数。

        3.实现思路：传送锚点

                (1).首先准备一个状态list：status ，status的前两个初始是False 对于0和1，后面

                    初始都是True

                (2).status[i] 为True时：表示i是素数 反之就是合数

                (3).然后用i遍历 2 到 n ,判断n以内的i是不是素数，是素数就改变状态

                (4).核心思想是利用最小素数因子排除素数：

                        只要一个数是素数的倍数，那么这个数一定是合数

                (5).最小素数因子的概念：15的素数因子是3 5 ，所以最小素数因子是 3 

5.代码（Python）

#利用欧拉筛 快速筛选包含n的n以内的所有素数
def euler_sieve(n):
    primes=[]
    status = [False] * 2 + [True] * (n - 1)
    for i in range(2,n+1):
        if status[i]:
            primes.append(i)
        for pj in primes:
            if pj * i >n:
                break
            status[pj*i]= False
            if i % pj == 0:
                break
    return primes

while True:
    n =int(input())
    if n ==0:
        break
    else:

        #kk表示筛选好的素数表
        kk=euler_sieve(n)

        #madiff表示当前最大差值
        maxdiff=0

        #maxlist用来保存每个最大差值所对应的i，i以append的方式添加在末位，所以遍历结束之后，末位的i一定就是我们要找的i
        maxlist=[]
        for i in kk:
            if n-i in kk:
                if abs(n-i-i)>maxdiff:
                    maxdiff=abs(n-i-i)
                    maxlist.append(i)
    maxi=maxlist.pop()
    print("{0} = {1} + {2}".format(n,maxi,n-maxi))