在几天前写了一篇最小生成树的文章

今天再讲解一下图论的另一个算法：拓扑排序

注：今天只讲解kahn算法，各位如果对dfs算法有需求可联系我进行讲解

说到拓扑排序，不得不先了解下拓扑是个什么东东

拓扑，它是一种结构

网络拓扑结构是指把网络电缆等各种传输媒体的物理连接等物理布局特征，通过借用几何学中的点与线这两种最基本的图形元素描述，抽象地来讨论网络系统中各个端点相互连接的方法、形式与几何形状，可表示出网络服务器、工作站、网络设备的网络配置和相互之间的连接。它的结构主要有总线型结构、星型结构、环型结构、树型结构、网状结构。 [3] 

计算机网络的拓扑结构分析是指从逻辑上抽象出网上计算机、网络设备以及传输媒介所构成的线与节点间的关系加以研究的一种研究方式。在进行计算机网络拓扑结构设计的过程中，通过对网络节点进行有效控制，对节点与线的连接形式进行有效选取，已经成为合理计算机网络拓扑结构构建的关键。设计人员对计算机网络拓扑结构进行有效选择，可以在很大程度上促进当前网络体系的运行效果，从根本上改善技术性能的可靠性、安全性。

                                                                                                        ————百度百科

拓扑本身实在是太复杂了，简而言之就是网络中各个站点相互连接的形式

还是说回我们的拓扑排序：

拓扑排序的介绍：

他是对一个图进行一个遍历，如果他是DAG（有向无环图），则生成一个序列，否则便可发现这个图有环路

这么说还是太抽象了，根本听不懂

还是画个小图：

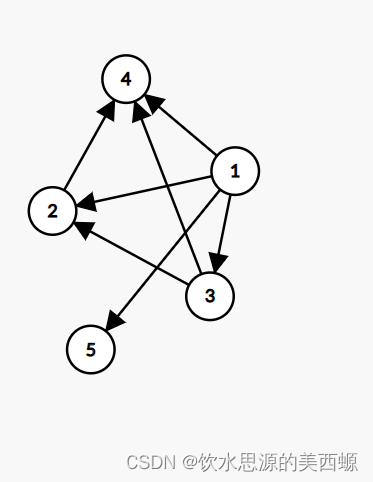
 一个很典型的DAG

第一步：定义一个队列，找出入度为0的点并入队

这个图中入度为0的点就是1

将他入队

并将他在图中删除

这时可以发现：2 3 4 5这些点的入度各减一，也就变成了这样：

。。。就变成了这样

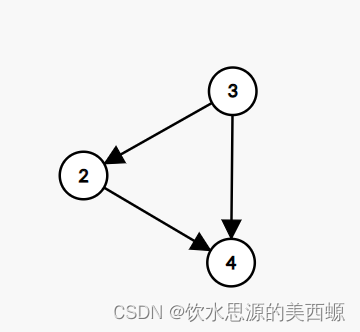
 继续刚才的步骤，寻找入度为0的，也就是3

 别嫌烦，继续重复步骤

就只剩一个点4了，这就证明这个图是DAG

有些同学不理解，为什么要寻找入度为0的

我们举一个反例：

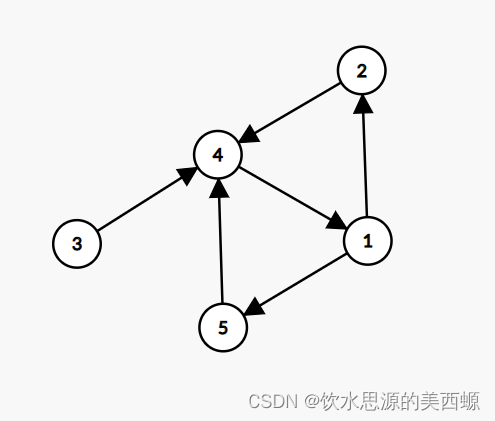
依然重复上面的步骤：

 

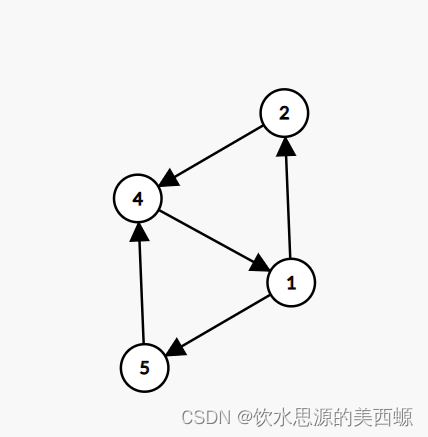
细心的同学会发现，不能重复上面的步骤了，所以它不是DAG

 

可还是刚才的问题：为什么要寻找入度为0的点？

首先我们要明确入度代表什么意思？

一个结点有入度，说明他是某某点的祖孙

所以说：入度为零代表他是目前的祖先（最高的祖先）

那么如果一个图找不到祖先了，那说明什么？一定有回路啊！、

现在同学们明白为什么要进行这样的操作了吧

接下来就是代码了：

我们拓扑排序继续采用链式前向星的存储方式

这个博主讲的不错[doge]

不懂的同学及时进行查看，本篇文章不对链式前向星做任何的讲解，如果有问题也可即使私信我

写任何题目的时候都要先写主函数

但是我们讲解的是算法，而不是具体题目，所以我们只出示kahn算法

按照刚才的思路，同学们自己先写一下

这里直接就给标程了

还是那句话，有任何不懂的随时评论区或私信我

void kahn(){
	queue<int> q;
	for (int i=1;i<=n;i++)
	{
		if (din[i]==0){
			q.push(i);
			printf("%lld ",i); 
		} 
	}//入度为0则进队列 
	
	while(!q.empty()){
		int u=q.front();
		q.pop();
		for (int i=adj[u];i;i=e[i].next){
			int v=e[i].to;
			din[v]--;
			if (din[v]==0){
				q.push(v);
				printf("%lld ",v);
			}
		}
	}
}