系列文章目录

文章目录

系列文章目录
前言
一、迷宫是什么？
二、迷宫的生成
- 迷宫的数据结构
- - 二维数组
  - 图
- Prim算法生成地图
- - 什么是Prim算法？
  - 使用Prim对迷宫生成的实现
三、迷宫的解法
- 深度优先遍历（DFS）

前言

前几天刷抖音刷到一个迷宫解法，觉得很有意思，想把迷宫解法好好玩玩分析一下，发现里面内容和学问多着呢，是一个非常有意思的主题。除了有如何找到迷宫从入口到出口的路径的玩法，还有如何生成一个迷宫的玩法。玩迷宫之前，首先我们要弄清楚一个问题，迷宫是什么？只有当我们弄清楚了迷宫的定义，才能玩好迷宫。

一、迷宫是什么？

迷宫是一个由格子或单元组成的矩形网格，其中包含一些可行走的路径和墙壁。迷宫通常具有一个入口和一个或多个出口，玩家的目标是从入口找到通向出口的路径。迷宫中的路径应该是连通的，所有的网格都应该是可达的，并且不应该包含环路。

二、迷宫的生成

根据上面迷宫的定义，大概就能明白什么是迷宫了。现在问题来了，应该如何生成一个随机的迷宫呢。当然生成之前，更应该解决的问题是迷宫的数据应该如何保存呢？用什么数据结构呢？

迷宫的数据结构

能很快想到的就是二维数组。还有什么数据结构呢？根据迷宫的定义可以想到，用图也可以表示一个迷宫。

二维数组

二维数组是一种非常直观的方式来表示迷宫。每个元素可以代表迷宫的一个单元格，值可以表示该单元格的状态，例如，是否是墙壁，是否已经被访问过等。例如，我们可以使用0表示空白单元格，1表示墙壁。

如果是使用二维数组，又有一个问题，如果是一个 $3 * 3$ 的迷宫
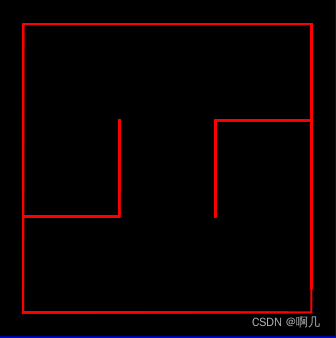
在这里插入图片描述
也就是这样一个迷宫，那应该使用多大的二维数组呢？int[n][n]，n应该是多少呢？也是3吗？如果不清楚，那我再将这个迷宫地图转换成块状的地图。

这两个是相同的地图，这时候是不是更明朗了？如果一个 $3 * 3$ 的迷宫地图，应该使用二位数组int[7][7]，也就是一个 $n * n$ 的迷宫地图，要使用int[n*2+1][n*2+1]的二维数组。而且如果迷宫地图每个网格都是可达的话，也就是二维数组初始状态就有很多数组为0的数。那二维数组初始时候应该是什么样呢？我写了一个生成地图的算法，用的是Prim算法。
这是我用javaFX做的一个展示效果，迷宫地图是 $10 * 10$ 的
请添加图片描述
这时候是不是就很清晰了，二维数组初始的状态，而生成迷宫地图要做的就是打破单元格之间的墙壁。让每个房间都变成联通的。

图

迷宫也可以被视为一个图，其中每个单元格是一个节点，如果两个单元格之间没有墙壁，那么这两个节点之间就存在一条边。这种表示方式对于使用图算法（如深度优先搜索或广度优先搜索）来解决迷宫问题非常有用。（还没实现，以后实现了再补充。。。）

Prim算法生成地图

什么是Prim算法？

Prim算法是一种用于生成最小生成树的贪心算法。最小生成树是一个图中的一个子图，它包含了图中的所有顶点，并且是所有可能的生成树中总权值最小的。生成树是一个无环的连通子图。

Prim算法的基本步骤如下：

初始化：从图的所有顶点中任意选择一个顶点作为起始点。
选择边：在已经访问过的顶点（已经在生成树中的顶点）的所有邻边中，选择一条权值最小的边，该边连接的另一顶点未被访问过。
添加顶点：将这条边的另一顶点加入到已访问的顶点集合中（即加入到生成树中）。
重复步骤：重复步骤2和3，直到所有的顶点都被访问过。

这个过程会生成一个最小生成树，其中包含了原图中的所有顶点，并且所有边的总权值最小。

使用Prim对迷宫生成的实现

对于迷宫地图的生成来说，迷宫初始化为0（迷宫的可达方格）的值就是图的顶点，而地图需要打破的方格之间的墙壁，也就是边。生成一个迷宫地图。我们要做的就是选择可以打破的边，直到所有方格都被访问。

    public int[][] generateMaze(int[] start) {
        initMaze();
        candidates.clear();
        //存储候选者<候选边，候选点>
        candidates.addAll(getCandidates(start));
        while (candidates.size() > 0) {
            int index = new Random().nextInt(candidates.size());
            Candidate current = candidates.get(index);
            if (!isCandidate(current)) {
                candidates.remove(current);
                continue;
            }
            maze[current.verge[0]][current.verge[1]] = 0;
            candidates.remove(index);
            List<Candidate> newCandidates = getCandidates(current.node);
            candidates.addAll(newCandidates);
        }
        return maze;
    }